Lesson 4
| Site: | MoodleHUB.ca 🍁 |
| Course: | Math 20-3 SS |
| Book: | Lesson 4 |
| Printed by: | Guest user |
| Date: | Tuesday, 2 December 2025, 7:01 AM |
Description
Created by IMSreader
1. Lesson 4
Module 6: Surface Area
Lesson 4: Changing Surface Area by Changing Linear Dimensions
Focus

iStockphoto/Thinkstock
Wearing matching family outfits may not appeal to you now, but as a kid it might have been kind of fun. When seamstresses or clothiers make similar pieces of clothing in smaller sizes, they require new height and width measurements. If a kid’s knitted hat has half the diameter of the matching hat for the father, would the kid’s version use half the material? Would it be half the cost to buy too?

both: iStockphoto/Thinkstock
In this lesson you will explore how the surface area of an object changes when you introduce changes to its linear dimensions. A linear dimension is a measure of distance indicating an object’s width, length, height, or diameter.
Lesson Question
- What is the effect on an object’s surface area when its linear dimensions are altered?
Assessment
Your assessment for this lesson may include a combination of the following:
- course folder submissions from the Try This and Share sections of the lesson
- your contribution to the Mathematics 20-3: Glossary Terms and the Formula Sheet
- Lesson 4 Assignment (Save a copy of your lesson assignment to your course folder now.)
- the Project Connection
Materials and Equipment
- calculator
1.1. Launch
Module 6: Surface Area
Launch
This section checks to see if you have the necessary background knowledge and skills required to successfully complete Lesson 4.
Complete the following Are You Ready? questions. If you have difficulty or any questions, visit Refresher for a review or contact your teacher.
1.2. Are You Ready?
Module 6: Surface Area
Are You Ready?
- List the first five perfect squares. Answer
- A large square has sides that are twice as long as the sides of a small square. How many times larger in area is the large square than the small square?
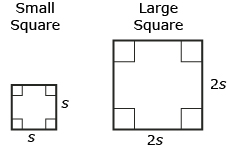
Answer
- The base and height of a large parallelogram are three times those of a small parallelogram. How many times larger is the area of the large parallelogram than that of the small parallelogram?
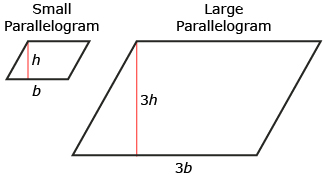
Answer
- The large circle has a radius of 25 cm, and the small circle has a radius of 5 cm. The large circles’ radius is 5 times longer than the small circle. How many times larger is the area of the large circle than that of the small circle?
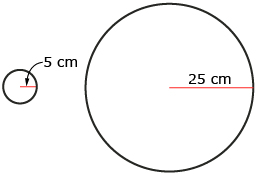
Answer
- The area of a two-dimensional shape is 5 in2. The linear dimensions of a similar larger shape are 10 times as large. How many times larger is the area of the larger figure than that of the smaller figure? Answer
If you answered the Are You Ready? questions without any issues, move on to Discover.
If you had some difficulty with the Are You Ready? questions, complete Refresher.
1.3. Refresher
Module 6: Surface Area
Refresher
If you don’t know the answers in Are You Ready?, or if you require more information, work through the following activities to review perfect squares, linear scale factors, and area scale factors.
Perfect Squares
|
|
Linear Scale Factors and Area Scale Factors
|
|
 |
|
Go back to Are You Ready? and try the questions again. Contact your teacher if you continue to have difficulty with the questions.
1.4. Discover
Module 6: Surface Area
Discover
In Launch you reviewed how the area of two-dimensional shapes changed when their linear dimensions increased or decreased by a factor. You may have noticed the following:
- If you doubled the length and width of a rectangle, its area increased 22, or four, times.
- If you tripled the dimensions in a parallelogram, its area increased 32, or nine, times.
- If you increased the radius of a circle by a linear factor of 5, its area increased 52, or 25 times.
Does changing the linear dimensions have the same effect on surface area as it does on area?
In Try This 1 you will investigate how changing the linear dimensions (length, width, and height) of three-dimensional objects changes their surface area.
Try This 1
How does the surface area of a cube change when its dimensions are doubled, tripled, or quadrupled?
Step 1: Click on the button to the left to open the “Exploring Surface Area, Volume, and Nets – Explore It” applet. Choose the rectangular prism from the list of objects and make sure that “Surface Area” is selected. Create a cube with these dimensions: length = 1 m, width = 1 m, and height = 1 m. Review the calculation for the surface area and record the surface area in the third column of a chart similar to the one that follows.
Step 2: Double the dimensions of the cube—in other words, the dimensions are changed by a linear scale factor of 2. The new dimensions should be length = 2 m, width = 2 m, height = 2 m. Determine the surface area and record it in the chart.
Step 3: Change the dimensions of the original cube by a linear scale factor of 3. In other words, triple each dimension of the original cube. Determine the surface area and record this information in the chart.
Step 4: Change the dimensions of the original cube by a scale factor of 4. Determine the surface area and record this data in the chart.
| Change to Dimensions | Linear Scale Factor | Actual Dimensions | Surface Area | Surface Area Scale Factor
|
| Original | 1 | 1 × 1 × 1 | ||
| Double | 2 | 2 × 2 × 2 | ||
| Triple | 3 | |||
| Quadruple | 4 |
Now, based on your investigation, answer the following questions.
- Calculate the surface area scale factor for each change in cube dimensions by using the following formula.
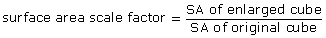
- What is the relationship between the linear scale factor and the surface area scale factor?
- Based on the relationship you identified in question 2, answer the following questions.
- If the cube’s dimensions increased by a linear scale factor of 10, by what scale factor must the surface area of the cube increase?
- If the cube’s dimensions increased by a linear scale factor of k, by what scale factor must the surface area of the cube increase?
- If the cube’s dimensions increased by a linear scale factor of 10, by what scale factor must the surface area of the cube increase?
- Are you surprised by what you found? A cube has three dimensions—length, width, and height—but the linear scale factor is squared, not cubed, to find the surface area scale factor. Use an example to explain why this happens.
![]() Save your responses in your course folder.
Save your responses in your course folder.
Share 1
Share your responses to the questions in Try This 1 with a classmate or with a group of people.
![]() If required, save a copy of your discussion in your course folder.
If required, save a copy of your discussion in your course folder.
1.5. Explore
Module 6: Surface Area
Explore
In Discover you examined the relationship between the linear scale factor (the number by which each dimension is multiplied) and the surface area scale factor of a cube.
You may have noticed that the surface area changed by a scale factor equal to the linear scale factor squared. The following equation summarizes this relationship:
area scale factor = (linear scale factor)2
So, for example, if you multiplied each of the dimensions of a cube by a factor of 5, the area of the new cube would be 52, or 25, times larger than the original prism.
Does this relationship apply to all three-dimensional objects? You will investigate this question in Try This 2.
Try This 2
- Step 1: Click on the button to open the Exploring Surface Area, Volume, and Nets—Explore It applet.
Step 2: On both the left and right sides of the screen, choose the rectangular prism from the list of objects and make sure you've got “Surface Area” selected. Set the dimensions on the left and right sides as indicated in the following chart. Determine the surface area scale factor for the rectangular prism the same way you did in Try This 1. Record the surface area scale factor in a chart like the one shown below.
Step 3: Repeat Step 2 for each 3-D object listed in the chart. Record the surface area scale factor for each object.
Object Left Dimensions Right Dimensions Linear Scale Factor Surface Area Scale Factor

Rectangular Prism 2 m × 2 m × 2 m 6 m × 6 m × 6 m 3 Rectangular Pyramid 5 m × 5 m × 5 m 10 m × 10 m × 10 m 2 Triangular Prism 2 m × 2 m 6 m × 6 m 3 Cylinder 2 m × 2 m 8 m × 8 m 4 Cone 5 m × 5 m 10 m × 10 m 2
-
Blowing bubbles is a favourite pastime for children of all ages. One bubble has a diameter of 2 cm. A second bubble has a diameter of 6 cm.

Lifesize/Thinkstock
- Use the formula
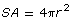 to calculate the surface area of each bubble. Round to the nearest tenth.
to calculate the surface area of each bubble. Round to the nearest tenth.
surface area of small bubble =
surface area of large bubble =
- Compare the surface area of the large bubble to the surface area of the small bubble. What do you notice?
- What linear scale factor is applied to the small bubble to get the large bubble?
- What surface area scale factor is applied to the small bubble to get the large bubble?
- Use the formula
![]() Save your responses in your course folder.
Save your responses in your course folder.
Share 2
Share your responses to the questions in Try This 2 with a classmate or with a group of people. Discuss the following question:
- How did your observations of prisms, pyramids, cylinders, cones, and spheres compare with your observations of the cube in Discover? Did you see a similar relationship between the linear scale factor and the surface area scale factor?
1.6. Explore 2
Module 6: Surface Area
Work through the following example.
 Comstock/Thinkstock
Comstock/Thinkstock Example
- How many times more icing would be needed for a wedding cake if it were made 1.5 times larger in diameter and 1.5 times higher? Assume the icing would be the same thickness.
- If you just wanted to double the icing, how many times larger in diameter and height would you have to make the larger cake? Round your answer to one decimal place.
Solution
- The scale of the larger cake = 1.5 × the smaller cake
Linear scale factor = 1.5
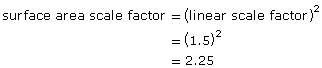
To ice the larger cake, you would need 2.25 times as much icing as you would to ice the smaller cake.

To double the amount of icing, the larger cake would be about 1.4 times larger than the smaller cake in height and diameter.
Self-Check 1
- Two cones are similar in shape. The small cone has a radius of 10 cm and a height of 8 cm. The large cone is 16 times larger in surface area than the small cone. What is the radius and height of the large cone? Answer
- The amount of material used to make the small teddy bear is 2 ft2. The amount of material used to make the identical looking, but larger, teddy bear is 6 ft2. What is the linear scale factor? Round to one decimal place.

Polka Dot/Thinkstock
Answer
- A model locomotive is built to 1:32 scale. How many times larger in surface area is the actual locomotive?

iStockphoto/Thinkstock
Answer
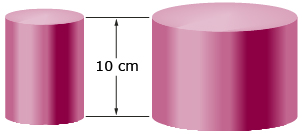
-
Natsuko is comparing open-ended cylinders. She notes that the radius of the second cylinder is double the radius of the first. She says that the surface area of the second cylinder is 22, or 4, times the surface area of the first cylinder.
It is now time to add new math terms to Mathematics 20-3: Glossary Terms.
In this lesson the new terms you will add are
- linear scale factor
- linear dimensions
- surface area scale factor
1.7. Connect
Module 6: Surface Area
Connect
Going Beyond

Hemera/Thinkstock
Deep snow on a roof can cause structural damage. Every winter you hear about roofs on shopping centres or arenas collapsing from the weight of accumulated ice and snow. Snow to a depth of 50 cm on a roof with an area of 100 m2 can weigh as much as 5 t (tonnes), which is the weight of a ten-passenger school bus.
How many school buses would 50 cm of snow on a roof be equivalent to if the roof were 3 times as wide and 3 times as long?
Project Connection
Modules 6 and 7 have a combined project. You should now be prepared to begin working on the surface area portion of the Module 6/7 Project: Clear the Roads! Read through the project document and make sure to pay close attention to how your project will be assessed. You can now begin working on Steps 1 to 5, which deal with surface area.
![]() Save all your project work in your course folder to submit at the end of Module 7.
Save all your project work in your course folder to submit at the end of Module 7.
Lesson 4 Assignment
Your lesson assignment contains some problems for you to solve using knowledge gained during the lesson. Now you will have the chance to apply the concepts and strategies that you have learned to a new situation. Show work to support your answers.
Open your Lesson 4 Assignment that you saved to your course folder and complete the questions.
1.8. Lesson 4 Summary
Module 6: Surface Area

Photo courtesy of NASA Science
Lesson 4 Summary
Balloons carry instruments to altitudes approaching 100 km. As they ascend, these balloons expand as atmospheric pressure decreases. Some balloons are designed to expand in dimensions by a factor of 100. How many times would the balloon's surface area increase?
The balloon in the photograph is being used to take equipment above 99% of the atmosphere.
In this lesson you investigated changes in surface area as linear dimensions change. You discovered that the surface area scale factor is directly related to the square of the linear scale factor. You applied this principle in a variety of problem situations.