Lesson 1
| Site: | MoodleHUB.ca 🍁 |
| Course: | Math 20-3 SS |
| Book: | Lesson 1 |
| Printed by: | Guest user |
| Date: | Tuesday, 2 December 2025, 7:05 AM |
Description
Created by IMSreader
1. Lesson 1
Module 7: Volume and Capacity
Lesson 1: Measuring and Estimating Volume and Capacity
Focus
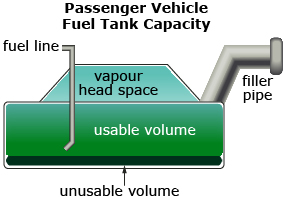
The cost of filling your vehicle depends on the price of fuel and the capacity of the fuel tank. If you fill your fuel tank when it is completely empty (running on fumes), you may need a litre or more than the quoted tank capacity. This may be because the tank capacity indicated in the manual does not include
- the volume of the tank below the fuel line
- the part of the tank designated as vapour space
- the capacity of the filler pipe
In this lesson you will estimate volume and capacity and explore the difference between these two measurements.
Lesson Questions
In this lesson you will investigate the following questions:
- What similarities and differences exist between volume and capacity?
- How are volume and capacity measured and estimated in the SI and imperial systems?
Assessment
Your assessment for this lesson may include a combination of the following:
- course folder submissions from the Try This and Share sections of the lesson
- your contribution to the Mathematics 20-3: Glossary Terms and the Formula Sheet
- Lesson 1 Assignment (Save a copy of your lesson assignment document to your course folder now.)
- the Project Connection
In this course you may come across Self-Check questions, Try This questions, and other activities that may or may not be assessed.
Remember that these questions and activities provide you with the practice and feedback that you need to successfully complete this course. You should respond to all the questions and place those answers in your course folder. Your teacher may wish to view the work that you have stored in your course folder to check on your progress and to see if you require assistance in some way.
Materials and Equipment
- calculator
- full bottle of juice, soft drink, or water
- graduated cylinder or measuring cup
Time
This lesson has been designed to take 150 minutes; however, it may take more or less time depending on how well you are able to understand the lesson concepts. It is important that you progress at your own pace based on your own learning needs.
1.1. Launch
Module 7: Volume and Capacity
Launch
This section checks to see if you have the necessary background knowledge and skills required to successfully complete Lesson 1.
Complete the following Are You Ready? questions. If you have difficulty or any questions, visit Refresher for a review or contact your teacher.
1.2. Are You Ready?
Module 7: Volume and Capacity
Are You Ready?
In the SI system, common units of volume include the following:
- cubic centimetre (a cube 1 cm on each side; cm3)
- cubic millimetre (a cube 1 mm on each side; mm3)
- cubic metre (a cube 1 m on each side; m3)
In the imperial system, some common volume units include the following:
- cubic inch (a cube 1 in on each side; in3)
- cubic foot (a cube 1 ft on each side; ft3)
- cubic yard (a cube 1 yd on each side; yd3)
-
- This object is composed of small cubes. How many small cubes are there altogether? Answer

PhotoObjects.net/Thinkstock
- If each small cube measured 1 cm on a side, what would the volume of the object be? What would the surface area, including the base, be? Answer
- If each small cube measured 1 in on a side, what would the volume of the object be? What would the surface area, including the base, be? Answer
- This object is composed of small cubes. How many small cubes are there altogether? Answer
- Which is larger—a cubic yard or a cubic metre? How do you know? Answer
- Another name for 1 cm3 is a millilitre (1 mL). What is the volume of 1 L of milk in cubic centimetres (cm3)? Answer

iStockphoto/Thinkstock
If you answered the Are You Ready? questions without problems, move on to Discover.
If you found the Are You Ready? questions difficult, complete Refresher to review these topics.
1.3. Refresher
Module 7: Volume and Capacity
Refresher
If you don’t know the answers to the Are You Ready? questions or require more information, work through the following activities to review volume and capacity:
Go back to Are You Ready? and try the questions again. Contact your teacher if you continue to have difficulty with the questions.
1.4. Discover
Module 7: Volume and Capacity
Discover

iStockphoto/Thinkstock
When you buy a bottle of juice or a soft drink, the packaging states the number of millilitres, or fluid ounces, in the container. What is this number referring to? Is it the amount of liquid in the bottle when you purchase the bottle, or is it the maximum amount of liquid the bottle can hold if filled to the very top? Would you use the term volume or capacity to describe this number?
You are going to investigate the difference between the terms volume and capacity using an unopened bottle of juice, water, or soft drink.
Try This 1
Step 1
iStockphoto/Thinkstock |
Look at the packaging of an unopened bottle of juice, soft drink, or water. In the first blank cell of the first row of a table like the one that follows, write the number of millilitres or fluid ounces written on the package.
|
Step 2
iStockphoto/Thinkstock |
Is this number the amount of liquid in the bottle, or is this the maximum amount the bottle can hold? In the second row of the table, put a checkmark in either the second-last cell or the last cell. |
Step 3
|
Does the number stated on the packaging relate to volume or capacity? In the second row of the table, write your response in the cell below your checkmark. |
Step 4
water bottle: iStockphoto/Thinkstock; beaker: Hemera/Thinkstock |
Open the bottle and empty the contents into a graduated cylinder (best choice), beaker, or measuring cup. Record the number of millilitres or fluid ounces of liquid in the bottle in the table’s first row. |
Step 5
iStockphoto/Thinkstock |
Fill the bottle to the very top with water. |
Step 6
water bottle: iStockphoto/Thinkstock; beaker: Hemera/Thinkstock |
Empty your graduated cylinder, beaker, or measuring cup, and then pour the water from your bottle into the graduated cylinder, beaker, or measuring cup (the same one as used before). In the first row of the table, record the maximum number of millilitres or fluid ounces it took to fill the bottle. |
| Number Stated on the Package | Amount of Liquid in the Bottle | Maximum Amount of Water the Bottle Can Hold | |
| Amount in Millilitres or Fluid Ounces | |||
| Prediction: Volume or Capacity? | |||
| Volume or Capacity? |
Based on your results, answer the following questions.
- Was the bottle filled right to the top before you opened it? Does it make any difference what was in the bottle? Carbonated versus non-carbonated? If not, can you think of any reasons why the bottle was not filled to the top?
- Compare the amount stated on the packaging to the amount of liquid originally in the bottle and the maximum amount of liquid the bottle can hold. Are any of these numbers equal or close to equal?
-
Look up the definitions for volume and capacity. You can read the definitions in the multimedia pieces provided: Volume, and Capacity. In the bottom row of the table, label each of the three columns as either volume or capacity.
- Define the terms volume and capacity in your own words. Provide an example of each word based upon what you learned in Try This 1.
![]() Save your responses in your course folder.
Save your responses in your course folder.
1.5. Explore
Module 7: Volume and Capacity
Explore
In Discover you defined volume and capacity in your own words. Even though the terms are used interchangeably, you will use the following definitions in Mathematics 20-3:
- volume: the amount of space a 3-D object occupies
e.g., the volume of juice or soft drink in the purchased bottle
- capacity: the maximum possible volume a container can hold
e.g., the maximum amount of water the bottle can hold
When determining volume or capacity, whether you are using SI, imperial measure, or United States Customary Units, it is important that you use the appropriate units. The more commonly used units for volume and capacity are shown in the following charts.
| Units for Volume | |
| Imperial | foot (ft3), cubic inch (in3), cubic yard (yd3), cubic mile (mi3) |
| SI (metric) | cubic millimetre (mm3), cubic centimetre (cm3), cubic kilometre (km3) |
| Units for Capacity | |
| Imperial | pint (pt), quart (qt), gallon (gal), cup (c), tablespoon (tbsp) |
| SI (metric) | millilitre (mL), litre (L) |
United States Customary Units (Imperial (US)) |
United States pint (pt (US)), United States quart (qt (US)), United States gallon (gal (US)) |
What do you notice about the difference between the units used for volume and those used for capacity? Look for patterns to help you remember these different charts.
In the United States, milk and juice are commonly sold in gallon, quart, and pint containers. Americans buy gasoline by the gallon. However, these American measures are different from the pints, quarts, and gallons used in Canada.
The United Stated quart and gallon are only ![]() as large as their Canadian imperial equivalents. This kind of inconsistency is a good reason to use metric units to quote volumes and capacities!
as large as their Canadian imperial equivalents. This kind of inconsistency is a good reason to use metric units to quote volumes and capacities!
Self-Check 1
Complete the Units of Volume and Capacity drag-and-drop activity to check your skills with units of volume and capacity. Click on the play button to get started.
You will use three different methods to help estimate volume and capacity:
- Method 1: Using Volume and Capacity Referents
- Method 2: Estimating Linear Dimensions
- Method 3: Water Displacement
1.6. Explore 2
Module 7: Volume and Capacity
Volume and capacity estimation skills are extremely important in any trade. These skills are used not only to determine which unit to use, but also to provide estimates of a project’s cost.
Method 1: Using Volume and Capacity Referents
Referents are used to form a mental image of common units of volume or capacity. For example, each edge of a sugar cube is approximately 1 cm long; therefore, a sugar cube can be used as a referent for a volume of 1 cm3. When you’re estimating the volume of a larger object, such as a calculator, you can imagine how many sugar cubes it will take to occupy the same space.

iStockphoto/Thinkstock

Try This 2
- Use a tape measure or ruler to measure objects of approximately the same volume as each of the cubic units listed in the chart. (A few examples have been filled in.) Pick objects you are likely to remember. Later, you will use these referents as mental images to estimate volume.
Units of Volume Referent 1 Referent 2 1 cm3 a sugar cube 1 m3 1 in3 1 ft3 1 yd3 a washing machine
- Look around your home or school to find containers (cans, milk jugs, paint cans) that have approximately the same capacity as each of the units in the chart. Later you will use these referents to estimate capacities.
Units of Capacity Referent 1 tbsp (tablespoon) 1 c (cup) 1 pt (pint) 1 qt (quart) a quart of motor oil 1 gal (gallon) 1 L (litre) 1 mL (millilitre)
Share 1
Share your charts from Try This 2 with a classmate or with a group of people. Add any new referents to your charts to help visualize volumes and capacities.
1.7. Explore 3
Module 7: Volume and Capacity
When you are estimating or measuring a large or small amount of material, you need to use a unit of appropriate size. Read through the next example to see why the size of the units you choose is important.
Example

iStockphoto/Thinkstock
Concrete, soil, sand, and gravel are often sold by the cubic metre. Why are these items not sold by the cubic centimetre?
Solution
The Cubic Metre to Cubic Centimetre image shows a comparison between a cubic metre and a cubic centimetre.
A cubic centimetre is only a fraction of the size of a cubic metre. In fact,
![]()
Concrete is sold in large quantities. It does not make sense to sell concrete or other similar building materials by the cubic centimetre. If this were done, customers would be buying millions of cubic centimetres of concrete, soil, sand, or gravel.
Self-Check 2
In Volume and Capacity you will identify measurements as either volume or capacity and you will choose the best unit for each estimation. Complete Volume and Capacity now.
Try This 3
Go back to your notes from Try This 2. Look at the referents you found to visualize 1 cm3 and 1 in3. Think of those objects as you work through Using Referents for Volume. In this activity you will use a referent to estimate the maximum volume a cereal box can hold.
Hemera Technologies/PhotoObjects/Thinkstock
- What was your estimate in cubic centimetres? In cubic inches?
- Which unit measure is easier to use in this case? Why?
- If you were asked for the capacity of the box, in what metric and imperial units would you give your answer?
![]() Save your responses in your course folder.
Save your responses in your course folder.
1.8. Explore 4
Module 7: Volume and Capacity
What about estimating the volume of a sphere? A unit cube wouldn’t be all that useful, so another method of estimating is needed.

Ryan McVay/Photodisc/Thinkstock
Method 2: Estimating Linear Dimensions
A second method of estimating volume and capacity is to use estimates of the object’s linear dimensions. In this method you round known measurements to numbers that are easier to work with. Then you use the volume formula to calculate an approximate volume or capacity.
Example
Assume you used a ruler to find the linear measurements of a dresser to be 3.2 ft wide, 4.1 ft tall, and 1.9 ft deep. Estimate the volume of space the dresser occupies in the room.
Solution
Round the measurements to numbers that are easier to work with.
3.2 ft wide rounds to 3 ft wide
4.1 ft tall rounds to 4 ft tall
1.9 ft deep rounds to 2 ft deep
Since the dresser has a rectangular prism shape, use the volume formula for a rectangular prism.
![]()
Substitute in the rounded measurements.
![]()
The dresser has an estimated volume of 24 ft3.
In the next example you will see how this method works for different-shaped objects. The following example uses a referent, instead of a ruler, to approximate the linear dimensions. Then the estimations are put into the appropriate volume formula.
Example

Miko would like to estimate the capacity of a slush cup. She does not have a ruler and finds it difficult to visualize how many sugar cubes occupy the same space. But Miko knows the nail on her forefinger is very close to 1 cm in width. She uses this referent to measure the cup’s height and diameter. Miko’s estimates are 20 cm in height and 8 cm in diameter. What is Miko’s estimate for the capacity of the slush cup?
Solution
The diameter is 8 cm. Therefore, the radius is 4 cm. To approximate the value of pi, 3 is used.
Since the cup’s shape is close to a cylinder, use the volume formula for a cylinder:
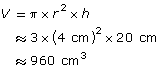
The cubic centimetre is a unit of volume. Since capacity is asked for, convert the unit to a unit of capacity.
Remember that 1 mL = 1 cm3; therefore, 960 cm3 = 960 mL.
Miko estimates the slush cup has a capacity of approximately 960 mL.
Self-Check 3
- Would you use cubic inches or cubic yards as an imperial unit of measure to determine the volume of your textbook? Use a referent to estimate the volume of your textbook. Answer
1.9. Explore 5
Module 7: Volume and Capacity
Method 3: Water Displacement
It is one thing to estimate the volume of a solid that can be approximated by a rectangular prism or cylinder. But what if the object is an irregular shape, such as the human body? To determine a person’s BMI, or body mass index, you need to know the volume of the person’s body. One approach to finding this volume is to use the principle involving the displacement of water described by Archimedes more than 2200 years ago.
Watch Water Displacement to Estimate Volume Measuring Butter, Margarine, or Shortening to see one method chefs use to accurately measure margarine, butter, and shortening.
It is now time to add new math terms, definitions, and examples and/or notes to your Mathematics 20-3: Glossary Terms document. Complete the missing pieces of the document, and save it to your desktop. Note that some terms, definitions, and examples and/or notes have already been provided in the document.
In this lesson the new terms you will add are the following:
- volume
- capacity
- United States Customary Units
- US gallon
- pint
- quart
- cup
- imperial gallon
- liquid ounce
1.10. Connect
Module 7: Volume and Capacity

iStockphoto/Thinkstock
Connect
Going Beyond
Volume and Capacity Puzzle
Renée Sawby has been given two urns. One urn holds 5 L and the other urn holds 3 L. She has been sent to collect exactly 4 L of water from the well. How will she accomplish this task?
Project Connection
You are now ready to complete Steps 6 and 7 of the Module 6/7 Project: Clear The Roads!
Lesson 1 Assignment
Your lesson assignment contains some problems for you to solve using the knowledge gained during the lesson. Now you will have the chance to apply the concepts and strategies learned to a new situation. Show work to support your answers.
Open the Lesson 1 Assignment that you saved to your course folder and complete the questions.
1.11. Lesson 1 Summary
Module 7: Volume and Capacity
Lesson 1 Summary

Tom Brakefield/Stockbyte/Thinkstock
Road construction involves the intensive use of heavy earth-moving equipment. In the photograph, a front-end loader is filling up a large truck. What volume of earth can be loaded in one scoop? What is the truck’s capacity? In this context, what units would you use to express volume and capacity?
In this lesson you examined volume and capacity and the units they are measured by. You practised estimating volumes and capacities using referents, and you learned that you can estimate volume and capacity by estimating dimensions or by using water displacement. You also explored situations when particular SI or imperial volume and capacity units would be used.