Lesson 2
| Site: | MoodleHUB.ca 🍁 |
| Course: | Math 20-3 SS |
| Book: | Lesson 2 |
| Printed by: | Guest user |
| Date: | Tuesday, 2 December 2025, 7:05 AM |
Description
Created by IMSreader
1. Lesson 2
Module 7: Volume and Capacity
Lesson 2: The Volume and Capacity of Prisms and Cylinders
Focus

DC Productions/Photodisc/Thinkstock
Fuel storage silos are common in Arctic communities. The tanks in the photograph are located near Inuvik, Northwest Territories. Although the tanks are not quite as strong as spherical containers, these cylindrical storage tanks are more economical to manufacture. These tanks can hold large volumes to ensure communities have sufficient fuel to carry them through the winter.
In this lesson you will explore how the volume and capacity of cylinders and prisms can be determined.
Lesson Questions
In this lesson you will investigate the following questions:
- How are the volume and capacity of cylinders and prisms calculated?
- How can you convert volume and capacity from one unit to another in SI and in the imperial system?
Assessment
Your assessment for this lesson may include a combination of the following:
- course folder submissions from the Try This and Share sections of the lesson
- your contribution to the Mathematics 20-3: Glossary Terms and the Formula Sheet
- Lesson 2 Assignment (Save a copy of your lesson assignment document to your course folder now.)
- the Project Connection
Materials and Equipment
- rulers (SI and imperial)
- calculator
1.1. Launch
Module 7: Volume and Capacity
Launch
This section checks to see if you have the necessary background knowledge and skills required to successfully complete Lesson 2.
Complete the following Are You Ready? questions. If you have difficulty or any questions, visit Refresher for a review or contact your teacher.
1.2. Are You Ready?
Module 7: Volume and Capacity
Are You Ready?
In previous mathematics courses you converted between the different volume units of the SI and imperial systems. In Mathematics 10-3 Learn EveryWare you used SI System Volume Conversion for SI volume units.
You used Imperial System Volume Conversion for imperial units.
You can also convert between units using dimensional analysis—converting dimensions before calculating volume.
- Convert 1 m3 to cubic centimetres. First use the conversion software. Then use dimensional analysis. Answer
- Convert 5 yd3 to cubic feet using dimensional analysis. Answer
- A US gallon is approximately 3.785 L. What approximate volume of milk can a US gallon-jug hold in cubic centimetres? Answer

© Mark Stout/28906245/Fotolia
- An inch is defined as exactly 2.54 cm. How many millilitres are there in a cubic inch? Answer
- Watch Engine Animation to see the operation of a four-cylinder engine. The engine’s displacement is shown in red at the end of the animation. What is the displacement, measured in cubic inches, of a 2-L engine? Round to the nearest cubic inch. Answer
If you answered the Are You Ready questions without problems, move on to Discover.
If you found the Are You Ready? questions difficult, complete Refresher to review these topics.
1.3. Refresher
Module 7: Volume and Capacity
1.4. Discover
Module 7: Volume and Capacity
Discover
In this section you will explore the volume of rectangular prisms and cylinders.
Try This 1
You will use Volume of Rectangular Prisms and Cylinders to complete Try This 1 and Share 1.
- Use Volume of Rectangular Prisms and Cylinders to complete a table like the following.
Dimensions Base of Rectangular Prism
1 cm × 1 cmBase of Rectangular Prism
1 cm × 2 cmBase of Rectangular Prism
1 cm × 3 cmBase of Cylinder
Radius
= 1 cm
Base of Cylinder
Radius
= 2 cm
Base of Cylinder
Radius
= 3 cm
Area of the Base (B) V
o
l
u
m
eHeight = 2 cm Height = 3 cm Height = 4 cm Height = 5 cm
- Look at your completed table. What do you notice about the prism’s volume as height is increased?
- What do you notice about the volume of the cylinder as height is increased?
- Use the table’s pattern to predict the volume of a rectangular prism with dimensions of 3 cm × 1 cm × 6 cm.
- Use the pattern in the table to predict the volume of a cylinder with dimensions of 3-cm base radius × 6-cm height.
- Remember that the formula for a rectangular prism is
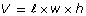 and that the area of the base of a prism is
and that the area of the base of a prism is 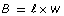 . Can you create another formula for the volume of a prism?
. Can you create another formula for the volume of a prism?
- Does this formula also work for the cylinder’s volume? Provide an example as proof.
Share 1
Share your responses to the questions in Try This 1 with a classmate or with a group of people.
- How does the formula you created in question 6 compare to your partner’s formula? Do your formulas work for all rectangular prisms and cylinders?
![]() Save a copy of your responses to Try This 1 in your course folder.
Save a copy of your responses to Try This 1 in your course folder.
1.5. Explore
Module 7: Volume and Capacity
Explore
In Try This 1 you developed and compared the volume formulas of a rectangular prism and a cylinder.

![]()
You may have noticed that the volume formulas for both rectangular prisms and cylinders are really the same:
![]()
This formula applies to any prism, regardless of the shape of its base.
In Try This 2 you will apply the formula V = B × h to a triangular prism.
Try This 2
How much glass is needed to make the following triangular prism? The dimensions of each end are shown in the diagram.
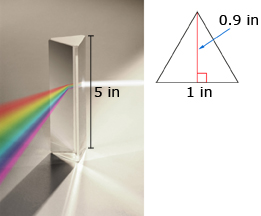
Comstock/Thinkstock
- What shape is the base of this prism?
- What formula will find the area of this shape?

- Calculate the area of the base.
- If the general formula to find the volume of any prism is (area of base) x (height), find the volume of this prism.
1.6. Explore 2
Module 7: Volume and Capacity
The next example shows how this same formula is used for a cylinder in a capacity situation.
Example

iStockphoto/Thinkstock
A cylindrical steel drum has a diameter of 22.5 in and a height of 33.5 in. If 1 gal = 277.42 in3, what is the capacity of the drum in gallons? Round to one decimal place.
Solution
The steel drum is cylindrical. The diameter is 22.5 in. Therefore, the drum radius is 11.25 in.
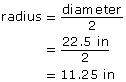
The formula for capacity of a cylinder is V = B × h. B is the area of the circular base, ![]() . So,
. So,
![]()
Substitute in the known values for r and h.
![]()
Convert cubic inches to gallons.
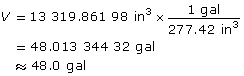
There are approximately 48.0 gal in the steel drum.
You may now want to add the volume and capacity formula for prisms and cylinders to the Formula Sheet.
Self-Check 1
- Open Prisms and Cylinders - Activity A. Complete the five assessment questions at the bottom of the gizmo.
Screenshot reprinted with permission of ExploreLearning.
- What is the volume of wood in a
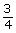 -in standard sheet of plywood? A sheet of plywood is 8 ft × 4 ft.
-in standard sheet of plywood? A sheet of plywood is 8 ft × 4 ft.  Answer
Answer

iStockphoto/Thinkstock
- Convert the volume of wood in the
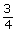 -in sheet of plywood from question 2 into cubic inches. Answer
-in sheet of plywood from question 2 into cubic inches. Answer
- A wooden feed trough with trapezoidal ends has inside dimensions as shown in the following graphic.
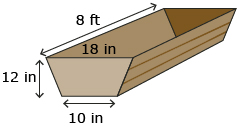
- Answer question 3 from “Build Your Skills” on page 145 of MathWorks 11. Answer
1.7. Explore 3
Module 7: Volume and Capacity
Solving for an Unknown Dimension Given the Volume or Capacity
Can you find a missing dimension when given the volume or capacity of a prism or cylinder and the other dimensions? It's time to try.
Example

iStockphoto/Thinkstock
The tractor trailer in the photograph is hauling a rectangular trailer with a capacity of 101.24 m3. If the width and height of the trailer are 2.5 m and 3 m, respectively, what is the trailer’s length? Work through the solution in Trailer Length.
iStockphoto/Thinkstock
Self-Check 2
- A cylinder is 1000 cm3 in volume. Its height is 20 cm. What is the cylinder’s radius? Round your answer to the nearest tenth of a centimetre. Answer
- A cylindrical paint can has a diameter of 7 in. How high does the can need to be to hold 1 gal (US)? Remember, 1 gal (US) = 231 in3. Round your answer to the nearest tenth of an inch. Answer

iStockphoto/Thinkstock
- Determine the height, in metres, of the following shipping container. Round your answer to two decimal places. Answer
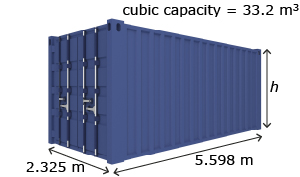
iStockphoto/Thinkstock
Try This 3
Volume and Capacity Puzzle
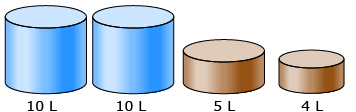
Miriam has two 10-L containers, a 5-L container, and a 4-L container. The two 10-L containers are full of water. By transferring water from container to container, she must end up with 2 L in the 5-L container and 2 L in the 4-L container. She must not spill or discard a drop of water. Help Miriam find a solution.
Share 2
Share your solution to the puzzle with a partner or with a group of people. How do your solutions compare? Many different solutions exist for this puzzle. Check your solutions to ensure each one works.
![]() Save your solution and one other group member’s solution in your course folder.
Save your solution and one other group member’s solution in your course folder.
1.8. Connect
Module 7: Volume and Capacity

Hemera Technologies/AbleStock.com/Thinkstock
Connect
Going Beyond
A cylindrical fish tank has a radius of 10 cm. Originally, there were no rocks in the tank. When rocks were added, the water level rose 3 cm, as shown in the image. To the nearest cubic centimetre, what is the volume of the rocks?
Project Connection
You are now ready to complete Step 8 of the Module 6/7 Project: Clear The Roads!
Remember to save all your work in your course folder to submit at the end of the module.
Lesson 2 Assignment
Your lesson assignment contains some problems for you to solve using the knowledge gained during the lesson. Now you will have the chance to apply the concepts and strategies learned to a new situation. Show work to support your answers.
Open the Lesson 2 Assignment that you saved to your course folder and complete the questions.
1.9. Lesson 2 Summary
Module 7: Volume and Capacity
Lesson 2 Summary

iStockphoto/Thinkstock
Piston-driven internal combustion engines are the lifeblood of today’s transportation industry. From trains to automobiles, without pistons and cylinders it would be difficult to maintain the society you know. Engine displacement is commonly given in cubic inches and litres. If you are mechanically inclined, you may wish to explore possible changes to engine design.
In this lesson you explored volumes of cylinders and prisms. To help remember the formulas you used, update your formula list.