Lesson 3
| Site: | MoodleHUB.ca 🍁 |
| Course: | Math 20-3 SS |
| Book: | Lesson 3 |
| Printed by: | Guest user |
| Date: | Tuesday, 2 December 2025, 6:58 AM |
Description
Created by IMSreader
1. Lesson 3
Module 7: Volume and Capacity
Lesson 3: The Volume and Capacity of Pyramids, Cones, and Spheres
Focus

iStockphoto/Thinkstock
Conical piles of sand and gravel are familiar sights at quarries near almost every community in Canada. Sand and gravel are used in road and rail-bed preparation, in asphalt and concrete, as fill, and in drinking-water filtration. Do you know that each year, per person, Canadians use over 15 m3 of aggregates? How would you estimate the volume of the conical pile in the photo?
In this lesson you will explore how the volume and capacity of pyramids, cones, and spheres are determined. You will determine these volumes in a variety of problem situations.
Lesson Questions
In this lesson you will investigate the following questions:
- How are the volume and capacity of pyramids, cones, and spheres calculated?
- How are volume and capacity formulas used in real-life situations?
Assessment
Your assessment for this lesson may include a combination of the following:
- course folder submissions from the Try This and Share sections of the lesson
- your contribution to the Math 20-3: Glossary Terms and the Formula Sheet
- Lesson 3 Assignment (Save a copy of your lesson assignment document to your course folder now.)
- the Project Connection
Materials and Equipment
- stiff paper or cardstock
- scissors
- tape
- geometry set
- calculator
1.1. Launch
Module 7: Volume and Capacity
Launch
This section checks to see if you have the necessary background knowledge and skills required to successfully complete Lesson 3.
Complete the following Are You Ready? questions. If you have difficulty or any questions, visit Refresher for a review or contact your teacher.
1.2. Are You Ready?
Module 7: Volume and Capacity
Are You Ready?
In previous mathematics courses you studied cones and cylinders. Do you remember the terms associated with these objects?
- Work through Pyramid Terms. Drag each term into the box that describes the associated part of the pyramid.

- Work through Cone Terms. Drag each term into the box that describes the associated part of the cone.
If you answered the Are You Ready? questions without problems, move on to Discover.
If you found the Are You Ready? questions difficult, complete Refresher to review these topics.
1.4. Discover
Module 7: Volume and Capacity
Discover
In this section you will investigate the relationship between the volume of a rectangular prism and the volume of another pyramid with the same base and height.
Try This 1
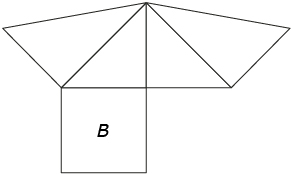
© Cathi Sanders and The Math Forum at Drexel University. Reproduced with permission.

© Cathi Sanders and The Math Forum at Drexel University. Reproduced with permission.
Step 1: Print off three copies of Pyramid Net on paper or cardstock.
Step 2: Cut out each net, fold along the lines, and then tape to form three identical pyramids, each with base B.
Step 3: Arrange the three pyramids so they fit together to form a rectangular prism. You may wish to use small pieces of tape to join the three pyramids together so that you can open and close the object.
Hint
Watch “How to Split a Cube Into 3 Identical Pyramids.”
- Use a ruler to measure the length and width of the base of the rectangular prism to the nearest tenth of a centimetre. Calculate the area of the base in square centimetres.
- Using the ruler, measure the height of the rectangular prism to the nearest tenth of a centimetre. Calculate the volume of space the prism takes up in cubic centimetres.
- From the volume of the rectangular prism, how could you find the volume of each pyramid? Calculate the volume of each pyramid.
- Use the results from questions 2 and 3 to determine a formula for finding the volume of each pyramid.
- What kind of rectangular prism did you form? How do you know?
Share 1
Share your responses to the questions in Try This 1 with a partner or with a group of people.
- Compare the formula you developed in question 4 with your partner’s formula. Describe any similarities and differences that may exist.
1.5. Explore
Module 7: Volume and Capacity
Explore
![]()
In Try This 1 you investigated the relationship between the volume of a rectangular prism and the volume of a pyramid with the same base, B, and height, h. You may have noticed that the volume of the pyramid is one-third the volume of the rectangular prism. This relationship can be seen in these formulas.
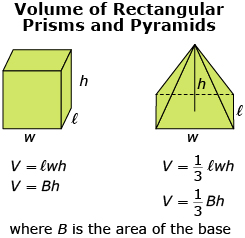
Example

Goodshoot/Thinkstock
Determine the volume of the Pyramid of Khafre. The base has a length of 215.5 m on each side and rises to a height of 136.4 m. Round your answer to the nearest 100 m3.
Solution
Find the area of the square base, B.
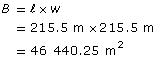
Find the volume of the pyramid. Substitute in the base, B.
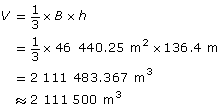
The volume of the Pyramid of Khafre is approximately 2 111 500 m3.
Self-Check 1
- A pyramid has the same base and height as a cube with 6 cm on each side. What is the volume of this pyramid?
 Answer
Answer
-
The interior of the crystal decoration in the photograph is a pyramid. The decoration is 6 cm deep.The top is a square that measures 8 cm on a side. What is the crystal’s capacity in millilitres? Round your answer to the nearest millilitre. Answer

1.6. Explore 2
Module 7: Volume and Capacity
The Volume and Capacity of Pyramids with Regular Polygon Faces
Regardless of the shape of the base of a prism or pyramid, the formula for volume remains the same. The base can be any shape that you can find the area of.
Example
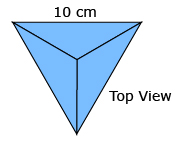
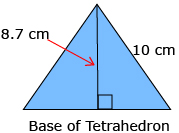
A tetrahedron is a pyramid made up of four equilateral triangles. Each side of this tetrahedron is 10 cm long.
The vertical height from apex to base is 8.7 cm.
When its net is folded out, the sides of each triangle are 10 cm long.
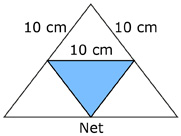
Determine, to the nearest cubic centimetre, the volume of this tetrahedron.
Solution
First, find the area of the triangular base, B.
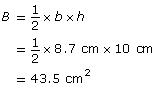
Use the formula for the volume of a pyramid. The perpendicular or vertical height, h, of the tetrahedron is 8.2 cm. The volume of the tetrahedron is approximately 119 cm3.
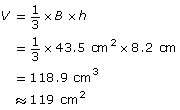
1.7. Explore 3
Module 7: Volume and Capacity
The Volume and Capacity of a Cone
You will now explore the volume of a cone. Watch “Measurement (Volume of a Cone): Part 1.”
Try This 2
- What is the formula for the capacity of a cylinder with a base of B units2 and a height of h units?
- What is the formula for the capacity of a cylinder with a circular base of radius r units and a height of h units?
- What is the relationship between the capacity of a cone and the capacity of a cylinder with the same height and base?
- Use your answers to questions 1 and 2 to determine two possible formulas for the volume of a cone.
- How are the formulas for the volumes of pyramids and cones similar?
![]() Save a copy of your responses to your course folder.
Save a copy of your responses to your course folder.
Share 2
Share your responses to the questions in Try This 2 with a classmate or group. After sharing the formulas you developed, answer the following question:
- How are the formulas for the volume of a cone and the volume of a pyramid similar?
![]() If required, save a copy of your discussion in your course folder.
If required, save a copy of your discussion in your course folder.
1.8. Explore 4
Module 7: Volume and Capacity
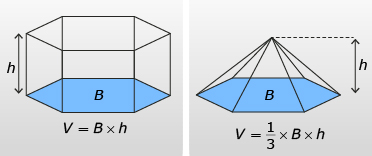
From Try This 2 you found that the volume of a cone is no different than the volume of any other pyramid. The volume is one-third the volume of a cylinder with the same base, B, and height, h.
Watch “Measurement (Volume of a Cone): Part 2,” and then examine the following image for a description of these formulas.
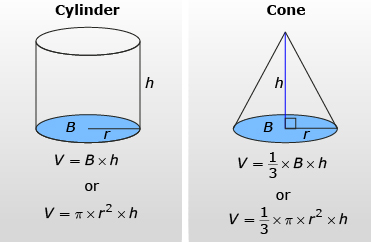
![]()
Note: The formulas may also be written as ![]() and
and ![]() .
.
1.9. Explore 5
Module 7: Volume and Capacity
Example
A conical pile of oats is 20 m in diameter and 5.3 m high. If there are approximately 27.5 bu (bushels) in a cubic metre, estimate the number of bushels of oats in the pile. Round your answer to the nearest 10 bu.

Photo courtesy of Inland Tarp & Liner, Inc.
Solution
If the diameter is 20 m, the radius is r = 10 m. The perpendicular height is h = 5.3 m.
Find the volume of the conical pile.
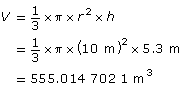
Convert cubic metres to bushels. You know that 1 m3 ≈ 27.5 bu.
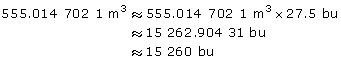
There are about 15 260 bu of oats in the pile.
Self-Check 2

iStockphoto/Thinkstock
Teepees vary in size. The teepee in the photograph is conical in shape. Its diameter on the ground is 16 ft, and its height is 13 ft. To the nearest cubic foot, what is the volume of air in the teepee? Answer
1.10. Explore 6
Module 7: Volume and Capacity
Example
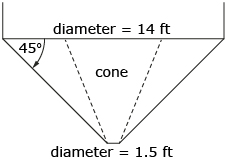
- If the 45° conical hopper of one of these grain bins has an upper diameter of 14 ft and a diameter at the shut-off of 1.5 ft, what is the hopper’s capacity? Round your answer to the nearest cubic foot.
- If an imperial bushel is approximately 1.284 4 ft3, how many bushels will the bin hold? Round to the nearest bushel.
Solution
- When you look at the hopper, you can visualize that the portion holding the grain is made up of a large cone with a diameter of 14 ft minus a small cone with a diameter of 1.5 ft. In order to find the capacity of the hopper, you need to find the capacity of the large cone and then subtract the capacity of the small cone.
To calculate these capacities, you still need to find the height of both cones. Use trigonometry to find the height of the large cone and the height of the small cone.
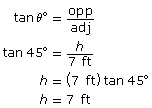
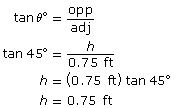
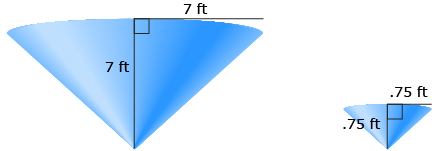
Find the volume of the large cone with radius = 7 ft and height = 7 ft.
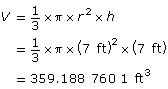
Do not round until you have subtracted the smaller cone. Rounding may introduce unwanted errors at this stage.
Find the volume of the small cone with radius = 0.75 ft and height = 0.75 ft.
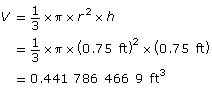
The volume of the conical hopper is the difference between these volumes.
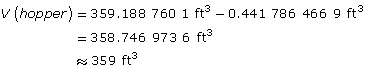
The hopper can hold approximately 359 ft3 of grain.
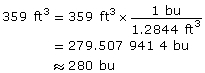
Self-Check 3
Work through Pyramid and Cones - Activity B. Complete the five assessment questions found at the bottom of the activity. You will check your answers in the activity.
Screenshot reprinted with permission of ExploreLearning.
1.11. Explore 7
Module 7: Volume and Capacity
The Volume and Capacity of a Sphere
In the last part of this section you will explore the volume of a sphere. Watch “Measurement 2 (Volume of a Sphere): Part 1.”
Try This 3
- What is the relationship between the volume of a sphere and the volume of a cylinder when both examples have the same diameter and height?
- Write a formula for the volume of a sphere. Use the formula for the volume of a cylinder.

- The height of the cylinder is twice the radius of the sphere, or h = 2r. In the formula you determined in question 2, substitute the value 2r in for h. Simplify the formula.
Share 3
Share your responses to the questions in Try This 2 with a classmate or with a group of people.
![]() Save a copy of your responses to Try This 3 in your course folder.
Save a copy of your responses to Try This 3 in your course folder.
V(cylinder) = π × r2 × h.
1.12. Explore 8
Module 7: Volume and Capacity
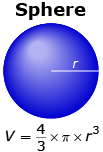
In Try This 3 you discovered that the volume of a sphere of radius r is given as ![]() . The formula may also be written as
. The formula may also be written as ![]() .
.
This formula can also be used to calculate capacity. Watch “Measurement 2 (Volume of a Sphere): Part 2” to review how the formula for the volume or capacity of a sphere relates to the formula for the volume of a cylinder.

iStockphoto/Thinkstock
Example
The diameter of a tennis ball is about 6.7 cm. To the nearest cubic centimetre, what is the volume of the tennis ball?
Solution

Hemera/Thinkstock
The diameter = 6.7 cm, so the radius, r, = 3.35 cm.
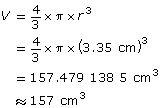
The volume of the tennis ball is approximately 157 cm3.
Example
For another example, turn to Page 154 of Mathworks 11 and read “Example 3.”
Self-Check 4
- The diameter of a cue ball is 2.25 in. What is the volume, in cubic inches, of a cue ball? Round your answer to one decimal place. Answer

AbleStock.com/Thinkstock
- A spherical tank that holds gas has an inner diameter of 8 m.

iStockphoto/Thinkstock
- What is the volume of gas the tank can hold, in cubic metres? Round to three decimal places. Answer
- Determine the capacity of the tank. If 1 m3 equals 1000 L, how many litres can the tank hold? Answer
- One United States gallon is equal to 3.785 L. To the nearest whole number, how many United States gallons does the tank hold? Answer
- What is the volume of gas the tank can hold, in cubic metres? Round to three decimal places. Answer
- Turn to page 158 of MathWorks 11. Answer question 5. Answer
You may now want to add the volume and capacity formulas for pyramids, cones, and spheres to your Formula Sheet.
1.13. Connect
Module 7: Volume and Capacity
Connect
Going Beyond
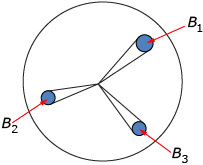
There is a clever way to determine the formula for the volume of a sphere from the formulas for the area of a sphere and the volume of a cone.
Take a little circular patch of area B1 on the surface of the sphere and form a cone by linking B1 to the centre of the sphere.
The volume of this small cone is V1.
Use the formula for the volume of a cone, ![]() , since the height of the cone is the radius of the sphere.
, since the height of the cone is the radius of the sphere.
Take a second patch, B2, and form a second cone. The volume is ![]() .
.
Keep following this procedure until you have covered the entire surface of the sphere with little patches.
The volume of the sphere will be the sum of all the volumes of these little cones.
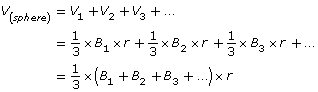
But B1 + B2 + B3 +… is simply the surface area of the sphere given by 4 × π × r2. So, substitute,
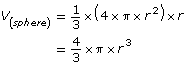
Project Connection
You are now ready to complete Step 9 of the Module 6/7 Project: Clear The Roads!
Lesson 3 Assignment
Your lesson assignment contains some problems for you to solve using the knowledge gained during the lesson. Now you will have the chance to apply the concepts and strategies learned to a new situation. Please show work to support your answers.
Open the Lesson 3 Assignment that you saved to your course folder and complete the questions.
1.14. Lesson 3 Summary
Module 7: Volume and Capacity
Lesson 3 Summary

AbleStock.com/Thinkstock
Earth’s sun is an average star in the universe. Scientists estimate the universe contains more than nine sextillion (21 zeros) stars. Mind you, Earth’s sun is almost a perfect sphere measuring 1 392 000 km in diameter. And, of course, for the last four billion years, all life on Earth owes its existence to this rather insignificant star!
In Lesson 3 you explored the volume and capacity of pyramids, cones, and spheres. What is the volume of Earth’s sun?