Lesson 4
| Site: | MoodleHUB.ca 🍁 |
| Course: | Math 20-3 SS |
| Book: | Lesson 4 |
| Printed by: | Guest user |
| Date: | Tuesday, 2 December 2025, 6:57 AM |
Description
Created by IMSreader
1. Lesson 4
Module 7: Volume and Capacity
Lesson 4: Applying Volume and Capacity Formulas
Focus
People wouldn’t survive without water. Water tanks are used around the world to store water and help create enough pressure to move the liquid to each person in the system. As you can see from the photos, water towers can come in a variety of different shapes. Can you identify any cylinders, cones, or spheres in the towers pictured?
Most objects are not pure spheres, pyramids, cones, cylinders, or prisms. Instead, objects are often combinations of many shapes. In this lesson you will apply volume and capacity formulas to a variety of practical problems, including composite figures.

cylinder tower: Comstock/Thinkstock; round tower: iStockphoto/Thinkstock; cone tower: iStockphoto/Thinkstock
Lesson Questions
In this lesson you will investigate the following questions:
- How are volume and capacity formulas applied to problems involving composite figures?
- How is formula manipulation used to find unknown dimensions?
Assessment
Your assessment for this lesson may include a combination of the following:
- course folder submissions from the Try This and Share sections of the lesson
- your contribution to the Mathematics 20-3 Glossary Terms
- Lesson 4 Assignment (Save a copy of your lesson assignment to your course folder now.)
- the Project Connection
Materials and Equipment
- calculator
1.1. Launch
Module 7: Volume and Capacity
Launch
This section checks to see if you have the necessary background knowledge and skills required to successfully complete Lesson 4.
Complete the following Are You Ready? questions. If you have difficulty or any questions, visit Refresher for a review or contact your instructor.
1.2. Are You Ready?
Module 7: Volume and Capacity
Are You Ready?
- Calculate
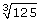 . Answer
. Answer
- In Lessons 2 and 3 you explored volume formulas for prisms and pyramids, for cylinders and cones, and for spheres. Review all these formulas by working through Volume Formula Review.

If you answered the Are You Ready? questions without problems, move on to Discover.
If you found the Are You Ready? questions difficult, complete Refresher to review these topics.
1.3. Refresher
Module 7: Volume and Capacity
Refresher
If you don't know the answers to the Are You Ready? questions or require more information, review the following.
For a review of the different volume formulas, work through Exploring Surface Area, Volume, and Nets (Object Interactive).
Go back to Are You Ready? and try the questions again. Contact your teacher if you continue to have difficulty with the questions.
1.4. Discover
Module 7: Volume and Capacity
Discover

pool: Jupiterimages/Comstock/Thinkstock; flowers: iStockphoto/Thinkstock
Landscapers deal with irregular shapes (composite figures) on a regular basis. Flower beds and swimming pools are two such examples.
A landscaper knows that calculating volume and capacity are important skills, since understanding these components helps determine the cost and time required to complete projects. For example, in order to install a swimming pool, the landscaper must estimate the volume of soil to be removed to fit the pool in the ground.
Try This 1
Look at the following custom-designed swimming pool.
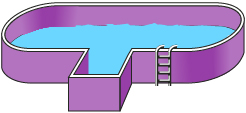
To determine the pool’s volume, you need to divide the composite figure into objects for which you have formulas.
- What simple 3-D objects will you divide the swimming pool into? Draw a diagram to show the divisions.
- What formulas will you use to determine the volume of each 3-D object?
- What dimensions will you need to calculate the volume of each object?
- What referents will you use to estimate those dimensions?
- What measuring tools will you need to determine the dimensions?
- What imperial units will you pick to calculate the volume?
Share 1
Share your responses to the questions in Try This 1 with a classmate or with a group of people.
- How did your divisions into simple objects compare with the divisions of your classmate? After viewing other divisions, would you change how you divided up the pool? Was there a division method that made the question easier to solve? If so, what was the division?
![]() Save a copy of your responses to Try This 1 in your course folder.
Save a copy of your responses to Try This 1 in your course folder.
1.5. Explore
Module 7: Volume and Capacity
Explore
In this section you will explore how volume formulas are applied to practical everyday problems. Many of these situations will involve composite figures.
Try This 2
Step 1: Open Composite 3D Figure.
Step 2: Read through Example Problem, Volume Solution One, and Volume Solution Two.
Step 3: Answer the questions that follow.
- What is the difference between Volume Solution One and Volume Solution Two?
- Which solution did you find easier to understand? Why?
![]() Save your responses from Try This 2 in your course folder.
Save your responses from Try This 2 in your course folder.
1.6. Explore 2
Module 7: Volume and Capacity
As you read through the following examples, think of different ways in which the composite figures could have been divided.
Example
A gelatine capsule containing medication is 1.11 cm in overall length and 0.491 cm in diameter. This capsule is a composite figure made up of a cylinder with two hemispherical ends. What is the capsule’s capacity in millilitres? Round your answer to two decimal places.
Note: A hemisphere is half a sphere, and 1 mL = 1 cm3.
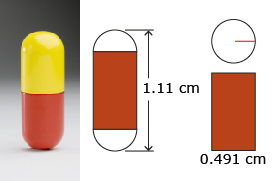
Creatas Images/Thinkstock
Solution
The two hemispherical ends form one sphere with a diameter of 0.491 cm.
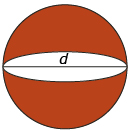
Creatas Images/Thinkstock
The radius, r, of the sphere and of the cylinder is one-half the diameter, d.
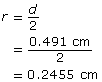
Find the height, h, of the central cylinder.
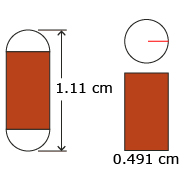
Creatas Images/Thinkstock

Find the total volume of the capsule.
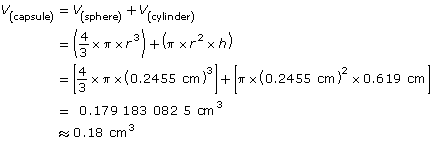
Because 1 mL = 1 cm3, the capacity of the capsule is about 0.18 mL.
Example
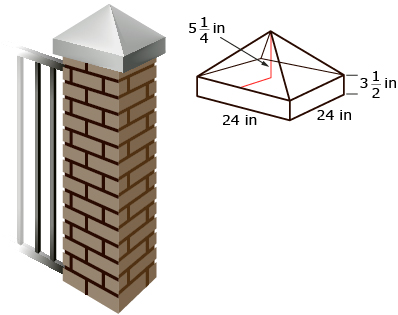
Consider the pillar shown.
- How much concrete is needed to make the top piece of the brick pillar?
- Concrete is sold in cubic yards. Convert the volume to cubic yards. Round your answer to three decimal places.
Solution
- The total volume of the pillar is made up of the volume of the rectangular (square) prism and the volume of the square pyramid (tetrahedron).
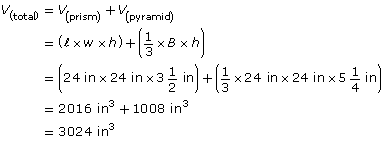
The volume of concrete needed is 3024 in3.
- To convert inches to yards use 1 in = 0.0278 yd.
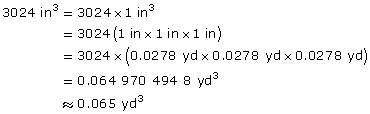
1.7. Explore 3
Module 7: Volume and Capacity
To review another example of finding the volume of composite figures, turn to pages 154 to 155 of MathWorks 11 and read through “Example 4.” As you read through this example, think about the following questions:
- What three-dimensional objects make up the composite figure?
- How does the volume of a hemisphere relate to the volume of a sphere?
Self-Check 1
![]()
- Turn to page 156 of MathWorks 11. Answer question 1 of “Build Your Skills.”
Answer
- Turn to page 160 of MathWorks 11. Answer question 3 of “Practise Your New Skills.” Answer
- Turn to page 162 of MathWorks 11. Answer question 9.a. Answer
Example
A number of practical problems involve determining an unknown dimension, such as height or radius, when the volume or capacity and the other dimensions are known. Work through The Radius of a Sphere. In this example the volume of a sphere is known but the radius is not. Notice how the formula for the volume of a sphere is rearranged to isolate and solve for the radius.
Self-Check 2
- What is the radius of a cylindrical container 10 cm high and 1000 cm3 in volume?
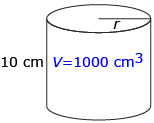
Answer
- A pyramid is 200 in3 in volume. The area of its base is 100 in2. What is the pyramid’s height? Answer
- An underground spherical water tank has a capacity of 2000 L. What is the interior diameter, in metres, of the tank? Round to two decimal places.
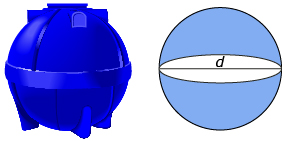
Answer
It is now time to add new math terms to Mathematics 20-3: Glossary Terms.
In this lesson the new terms you will add are
- composite figure
- hemisphere
1.8. Connect
Module 7: Volume and Capacity
Connect
Going Beyond
Volume is a key component of a vehicle’s engine power. Within the engine, there are cylinders with pistons that move up and down. When a piston moves from the top to the bottom of the cylinder, the piston sweeps air and/or fuel in and out. The amount of air and/or fuel swept depends on the diameter of the piston and cylinder as well as the distance the piston moves in the cylinder.
You can calculate the volume of air and/or fuel swept by each cylinder. This calculation is called engine displacement, and this volume determines the engine’s power. Following is an illustration of pistons and cylinders in a four-cylinder engine.

iStockphoto/Thinkstock
Turn to page 143 of MathWorks 11 and work through “Example 3” to gain more insight into how volume is a key engine component.
Project Connection
You are now ready to complete Step 10 of the Module 6/7 Project: Clear The Roads!
![]() Remember to save all your work in your course folder to submit at the end of the module.
Remember to save all your work in your course folder to submit at the end of the module.
Lesson 4 Assignment
Your lesson assignment contains some problems for you to solve using knowledge gained during the lesson. Now you will have the chance to apply the concepts and strategies learned to a new situation. Show work to support your answers.
Open the Lesson 4 Assignment that you saved to your course folder and complete the questions.
1.9. Lesson 4 Summary
Module 7: Volume and Capacity
Lesson 4 Summary

iStockphoto/Thinkstock
Open hopper cars are a type of freight car used to move coal across Canada. The bottom dump doors allow coal to be easily unloaded. How can you use your understanding of composite figures to estimate the capacity of each car? What objects can you identify that create the hopper cars in the photograph?
In this lesson you investigated composite figures and methods for determining each figure’s volume and capacity. You applied the formulas for the volume and capacity of common geometric figures to solve a variety of practical problems, such as manipulating volume formulas to solve for dimensions.