Lesson 5
| Site: | MoodleHUB.ca 🍁 |
| Course: | Math 20-3 SS |
| Book: | Lesson 5 |
| Printed by: | Guest user |
| Date: | Tuesday, 2 December 2025, 6:58 AM |
Description
Created by IMSreader
1. Lesson 5
Module 7: Volume and Capacity
Lesson 5: Scaling, Volume, and Capacity
Focus

iStockphoto/Thinkstock
Renting a truck to move your belongings can be tricky! If the truck is too big, you will have wasted money and fuel, and the extra room might allow your furniture and boxes to move around too much as you drive. If the truck is too small, you will waste time and fuel making multiple trips.
Many rental moving trucks are referred to by their lengths—a 14-ft, 17-ft, or 24-ft truck. In most cases, the height and width of these trucks are the same: only their lengths are different. How does this change in length affect the capacity of each truck?
Throughout Lesson 5 you will look at how volume and capacity are affected by changes in linear measurements.
Lesson Question
In this lesson you will investigate the following question:
- How does altering an object’s linear dimensions affect the object’s volume and capacity?
Assessment
Your assessment for this lesson may include a combination of the following:
- course folder submissions from the Try This and Share sections of the lesson
- Your contribution to the Mathematics 20-3 Glossary Terms and the Formula Sheet
- Lesson 5 Assignment (Save a copy of your lesson assignment to your course folder now.)
- the Project Connection
Materials and Equipment
- calculator
1.1. Launch
Module 7: Volume and Capacity
Launch
This section checks to see if you have the necessary background knowledge and skills required to successfully complete Lesson 5.
Complete the following Are You Ready? questions. If you have difficulty or any questions, visit Refresher for a review or contact your instructor.
1.2. Are You Ready?
Module 7: Volume and Capacity
Are You Ready?
- What are the first five perfect squares? Answer
- What are the first five perfect cubes? Answer
- Calculate
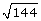 . Answer
. Answer
- A large cube has sides twice as long as the sides of a small cube. How many times larger in surface area is the large cube?
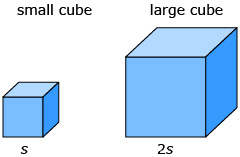
Answer
- If the radius of a sphere is tripled, how many times larger is the surface area of the large sphere than the surface area of the smaller sphere?
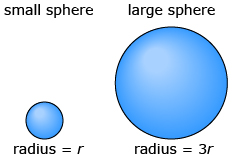
Answer
- Kayaks of the Inuit of the Central Canadian Arctic, such as the one shown, were built for speed to pursue caribou on lakes and rivers. The kayaks were covered with the skins of caribou or seal and were light, watertight, and manoeuvrable.
If a second kayak with the same proportions is constructed with double the surface area, how many times longer would the kayak be? Round your answer to one decimal place.

© Canadian Museum of Civilization Corporation
Answer
If you answered the Are You Ready? questions without problems, move on to Discover.
If you found the Are You Ready? questions difficult, complete Refresher to review these topics.
1.3. Refresher
Module 7: Volume and Capacity
Refresher
If you don't know the answers to the Are You Ready? questions or require more information, review the following activities.
Open Exploring Square Roots (Object Interactive) to review perfect squares.
Open Exponent to review the definition of an exponent.
To review scale factors and surface area, you may want to go back to Module 6 Lesson 4 of this course.
Go back to Are You Ready? and try the questions again. Contact your teacher if you continue to have difficulty with the questions.
1.4. Discover
Module 7: Volume and Capacity
Discover
In Try This 1 you will discover the relationship between linear dimensions—length, width, and height—and corresponding changes in volume. You have previously used Exploring Surface Area, Volume, and Nets (Object Interactive). In Try This 1 you will use the applet again to see how volume is affected when you change one, two, or all three dimensions by a linear scale factor.
Try This 1
Use Exploring Surface Area, Volume, and Nets (Object Interactive) to answer the following questions. Note that in each case of Rectangular Prism, the starting point is a single cube. When the scale factor is 1, the dimensions (length, width, and height) are all 1.
- Complete a table like the following. Some entries are filled in as examples.
Scale Factor Volume (in cm3) when the following dimension is multiplied by the linear scale factor
• only length
Volume (in cm3) when the following dimensions are multiplied by the linear scale factor
• length
• width
Volume (in cm3) when the following dimensions are multiplied by the linear scale factor
• length
• width
• height
1 (original cube) 1 1 1 2 2 4 8 3 4 k
If you need help answering the following questions, complete questions 1 and 2 in Are You Ready? This will help you see the pattern in the table.
- How is the volume affected if only the length is changed by a factor of k?
- How is the volume affected if both length and width are changed by a factor of k?
- How is the volume affected if all three dimensions are changed by a factor of k?
Share 1
Share and discuss your responses to the questions in Try This 1 with a classmate or with a group of people. Summarize your discussions by answering the following question:
- What is the relationship between changes in linear dimensions and the effects of the changes on volume?
![]() Save your responses to Try This 1 and a short summary of your discussion from Share 1 in your course folder.
Save your responses to Try This 1 and a short summary of your discussion from Share 1 in your course folder.
1.5. Explore
Module 7: Volume and Capacity
Explore
Architects need to know the effect of scale factor on volume when they make scale models of buildings. When doubling the dimensions of a flowerbed, gardeners need to know the effect of the scale factor on the flowerbed’s capacity in order to purchase the correct amount of soil.
In Discover you examined the relationship between the scale factor—the number by which each dimension is multiplied—and the volume of a cube. You may have discovered this information:
- If one dimension changed by a factor of k, the volume changes by a factor of k.
- If two dimensions are changed by the same scale factor of k, the volume changes by a factor of k2.
- If all three dimensions are changed by the same scale factor of k, the volume changes by a factor of k3.
So, if you multiply each dimension of a cube, for instance, by a factor of 5, the volume of the new cube would be 53, or 125 times, more than the original cube.
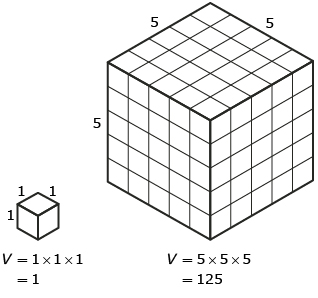
Does this relationship apply to all three-dimensional figures?
Try This 2
Open Investigating the Volume of Cylinders to help you answer the following questions. When the scale factor is 1, the cylinder radius and height are both equal to 1 m.
- Complete the following table. Some entries are filled in as examples.
Scale Factor Volume (in cm3) when
• only height
is multiplied by the linear scale factor
Volume (in cm3) when
• only radius
is multiplied by the linear scale factor
Volume (in cm3) when
• height
• radius
are multiplied by the linear scale factor
1 (original cylinder) 1

1

1

2 3 4 5 k
- How is the volume affected if only the height is multiplied by a scale factor of k?
- How is the volume affected if only the radius is multiplied by a scale factor of k?
- How is the volume affected if both the radius and height are multiplied by the scale factor of k?
-
The formula for the volume of a cylinder is
That fact can be shown as follows: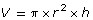 . If the cylinder height is increased to 2h but the radius remains the same, the new volume becomes 2V.
. If the cylinder height is increased to 2h but the radius remains the same, the new volume becomes 2V.

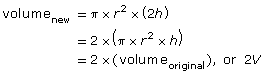
Show algebraically that, if the radius doubles, the new volume is 4 times the volume of the original.
![]() Save your responses from Try This 2 to your course folder.
Save your responses from Try This 2 to your course folder.
Share 2
Share your responses to the questions in Try This 2 with a classmate or with a group of people. Then discuss the following:
- What is the relationship between changes in the linear dimensions of cylinders and the effect of the changes on volume?
- How does this relationship compare to the relationship discussed in Share 1?
![]() If required, save a copy of your discussion in your course folder.
If required, save a copy of your discussion in your course folder.
1.6. Explore 2
Module 7: Volume and Capacity
Both Try This investigations in Lesson 5 showed that, for rectangular prisms and cylinders, the relationship between the volume scale factor and linear scale factor followed the same pattern. This relationship also holds true for all three-dimensional figures.
For all three-dimensional figures, keep the following information in mind:
If just one dimension changes,
volume scale factor = (linear scale factor)
If two dimensions change,
volume scale factor = (linear scale factor)2
If all three dimensions change,
volume scale factor = (linear scale factor)3
At this time, you may wish to include the volume scale factor and linear scale factor relationships in your Formula Sheet.
Example
A manufacturer of gasoline barrels was determining what effect changing dimensions would have on the capacity of the company’s cylindrical barrels. The company started with a barrel that had a capacity of 1 L.
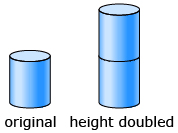
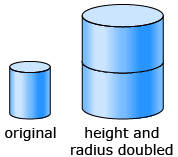
- What will the barrel’s capacity be if only the barrel’s height is doubled?
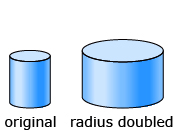
- What will the barrel’s capacity be if only the barrel’s radius is doubled?
- Calculate the barrel’s capacity if both the barrel’s height and radius are doubled.
Solution
-
If just the height is doubled, it is logical to see that the capacity is doubled. It is like putting another 1-L barrel on top of the original 1-L barrel. The manufacturer will have 2 L.
-
If the radius is doubled, it is like doubling both the length and width. So, the capacity will be 2 x 2, or 4, times as great. The barrel will have a capacity of 4 L.
This is easy to see if you look at the formula for the volume of a cylinder.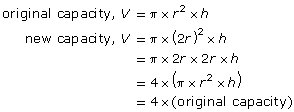
-
Remember what you learned in parts a. and b. If both the radius and height are doubled, you will have factors of 2 (for the height change) and 4 (for the radius change). The capacity will be
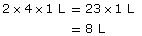

iStockphoto/Thinkstock
Self-Check 1
-
- How will the capacity of a swimming pool change if the pool’s length and width are tripled? Answer
- How will the capacity of a swimming pool change if the pool’s depth, length, and width are all tripled? Answer
- How will the capacity of a swimming pool change if the pool’s depth remains the same, but the length is doubled and the width is tripled? Answer
-
Jeremy is shopping for oranges. He notices that not all oranges are the same size. One orange is 1.5 times the diameter of another. How many times greater is the volume of the large orange? Answer
 Comstock/Thinkstock
Comstock/Thinkstock
-
A model train locomotive is built to 1:32 scale. How many times larger in volume is the actual locomotive? Answer
 iStockphoto/Thinkstock
iStockphoto/Thinkstock
- The planets in the solar system are all approximately spheres. If Uranus has a volume 64 times that of Earth, what is the relationship between the two planets’ radii? Answer
1.7. Explore 3
Module 7: Volume and Capacity
Suppose two three-dimensional objects are similar; that is, one is simply a scale factor of the other. If you know the dimensions of one of the objects, you can determine the dimensions of the other by using the scale factor.

Hemera/Thinkstock
Example
An aquarium manufacturer wishes to scale each dimension of a popular spherical bowl so the bowl has twice the capacity. What scale factor will be used? Round to two decimal places.
Solution
Since the bowls are spheres, changing the radius is equivalent to changing all three dimensions.
The new capacity is two times as large, so the capacity scale factor is 2.
(linear scale factor)3 = capacity scale factor
Let k be the scale factor.
(k)3 = 2
Take the cube root of both sides to eliminate the exponent on k.
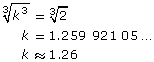
The bowl dimensions will be increased by a scale factor of 1.26 in order to double the capacity of the bowl.
Note: On some calculators you must use the following keystrokes to find a cube root of a number. To find the cube root of 2, press
![]()
Self-Check 2
- The manufacturer of conical paper cups wishes to make a cup that will hold four times the capacity of the best-selling cup. The manufacturer wants to retain the same cup proportions. The company will have to change all dimensions by the same scale factor. What scale factor should be used? Round to two decimal places.
Answer
- If the diameter of the original cup in question 1 were 6 cm, what would be the diameter of a cup that holds four times as much liquid? Round to the nearest tenth of a centimetre. Answer
1.8. Connect
Module 7: Volume and Capacity

Jupiterimages/Pixland/Thinkstock
Connect
Going Beyond
Some chocolate manufacturers offer “calorie-wise” bars by simply reducing the overall size of their regular bars.
A manufacturer intends to offer a calorie-wise bar by making a bar with only 80% of the length, width, and thickness of the regular bar. Assuming the same ingredients are used, by what percent are the calories reduced?
Project Connection
You are now ready to complete the Module 6/7 Project: Clear The Roads! Complete Steps 11 and 12 and then submit the entire project to your teacher.
![]() Remember to save all your work to your course folder and then submit the entire project to your teacher at the end of this lesson.
Remember to save all your work to your course folder and then submit the entire project to your teacher at the end of this lesson.
Lesson 5 Assignment
Your lesson assignment contains some problems for you to solve using knowledge gained during the lesson. Now you will have the chance to apply the concepts and strategies learned to a new situation. Show work to support your answers.
Open the Lesson 5 Assignment that you saved to your course folder and complete the questions.
1.9. Lesson 5 Summary
Module 7: Volume and Capacity
Lesson 5 Summary

Hemera/Thinkstock
Moving boxes come in a wide variety of shapes and sizes. Estimating the number of boxes you will need for a move can be quite a challenge. A box with a small capacity may be better for moving textbooks, but a box with a large capacity might be better for clothing.
A variety of box capacities and dimensions are needed when you move. In some cases a box twice as tall might be required to fit a lamp. How does this change to the box’s dimension affect the box’s capacity?
In this lesson you analyzed the change in volume and capacity as linear dimensions changed. You discovered that volume was affected depending on how many dimensions were increased by certain linear scale factors. Then you applied this principle to a variety of problem situations.