Lesson 4
| Site: | MoodleHUB.ca 🍁 |
| Course: | Math 30-1 SS |
| Book: | Lesson 4 |
| Printed by: | Guest user |
| Date: | Tuesday, 9 December 2025, 10:34 PM |
Description
Created by IMSreader
1. Lesson 4
Module 1: Function Transformations
Lesson 4: Combining Transformations
Focus
Some artwork is just one image manipulated over and over in slightly different ways. This graphic was made using stretches, reflections, and translations. Is it important in what order the transformations were applied? If you wanted to use a coordinate grid to help with these transformations, does it matter where you put the grid?

In this lesson you will learn to use multiple transformations on a function. You will also learn to relate the graph of a transformed function to its equation.
Lesson Outcomes
At the end of this lesson you will be able to
- sketch the graph of the function
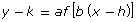 for given values of a, b, h, and k, given the graph of the function y = f(x)
for given values of a, b, h, and k, given the graph of the function y = f(x) - write the equation of a function, given its graph, which is a translation and/or stretch of the graph of the function y = f(x)
Lesson Questions
You will investigate the following questions:
- How can multiple transformations be applied to a function?
- How can you write the equation of a transformed function given the original graph?
Assessment
Your assessment may be based on a combination of the following tasks:
- completion of the Lesson 4 Assignment (Download the Lesson 4 Assignment and save it in your course folder now.)
- course folder submissions from Try This and Share activities
- additions to Formula Sheet
Materials and Equipment
- graph paper
1.1. Discover
Module 1: Function Transformations
Discover
Try This 1
Projectile motion simulators like the one that follows are common. Open “Golf Range” and experiment with the effects of using different angles and initial speeds. Turn on “Show paths” to see the trajectory of your ball. Press ![]() to shoot and
to shoot and ![]() to swing again.
to swing again.
- What general shape does the path always take?
- How does changing the speed or angle affect the shape?
- How can the path of a projectile be transformed into the path of another projectile?
- The projectiles in the simulator all followed a parabolic trajectory, which can be modelled by y = x2 after various transformations.
- Open Projectile Equation Matcher to explore the equations of these parabolas. The function
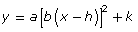 is given in red and its values of a, b, h, and k can be manipulated.
is given in red and its values of a, b, h, and k can be manipulated.
- Select projectile 1.
- Use the sliders to match the red function to the green projectile 1.
- Complete the following table.
Projectile
Value of
a
Value of
b
Value of
h
Value of
k
Description of How f(x) = x2 Was Transformed
1
2
3
4
- Open Projectile Equation Matcher to explore the equations of these parabolas. The function
![]() Save your responses in your course folder.
Save your responses in your course folder.
Share 1
With a partner or group, discuss the following question based on the table you created in Try This 1:
Is it possible for more than one equation to match a projectile path? Explain.
![]() If required, save a record of your discussion in your course folder.
If required, save a record of your discussion in your course folder.
1.2. Explore
Module 1: Function Transformations
Explore
In Try This 1 you saw that it was possible to perform stretches, reflections, and translations across the same function. When multiple transformations are used, the order in which they are applied is significant. Complete the following investigation to see how important order is.

Hemera/Thinkstock
Try This 2
Complete “Investigate the Order of Transformations” questions 1 to 7 on pages 32 and 33 of the textbook. A table similar to the following, which includes examples of transformations from some of the questions, may help you organize the information. Working on graph paper will be helpful for this exercise.
|
Transformation |
Sketch |
How do the two transformations compare? |
Does order matter? |
| Stretches | 1.b. vertical stretch, then horizontal stretch |
|
|
|
1.c. horizontal stretch, then vertical stretch |
|
|||
| Vertical Reflection and Translation | 3.b. reflection across the x-axis, then vertical translation |
|
|
|
3.c. vertical translation, then reflection across the x-axis |
|
|||
Horizontal Reflection and Translation |
5.b. reflection across the y-axis, then horizontal translation |
|
|
|
5.c. horizontal translation, then reflection across the y-axis |
|
|||
| Vertical Stretch and Translation | 7.a. vertical stretch, then vertical translation |
|
|
|
7.a. vertical translation, then vertical stretch |
|
![]() Save your responses in your course folder.
Save your responses in your course folder.
Share 2
With a partner or group, discuss the following questions based on the table you created in Try This 2.
- Is the order of stretching and reflecting important? Explain.
- Is the order of a horizontal translation and a reflection across the x-axis important? Explain.
- What order of translating, reflecting, and stretching do you think will be the easiest to use?
![]() If required, save a record of your discussion in your course folder.
If required, save a record of your discussion in your course folder.
1.3. Explore 2
Module 1: Function Transformations
You have seen that multiple transformations can be applied to a function. By starting with the stretched and reflected equation y = af(bx), translations can be added by replacing y with y − k and x with x − h to give ![]() This is sometimes written as
This is sometimes written as ![]()
You have also seen that switching the order of a translation and a stretch or a reflection affected the outcome of the transformation. To use an equation of the form ![]() apply the stretches and reflections before the translations.
apply the stretches and reflections before the translations.

The next example shows how stretches and translations can be applied to the same function.
Read “Example 1” on pages 34 and 35 of the textbook.
Self-Check 1
Complete “Your Turn” from “Example 1” on page 35 of the textbook. Answer
Watch Graphing Transformations to see how a function of the form ![]() can be graphed from y = f(x).
can be graphed from y = f(x).
Read “Example 2” on page 36 of the textbook. Pay attention to how mapping notation is used to describe what happens to individual points.
Self-Check 2
- Complete “Your Turn” from “Example 2” on page 37 of the textbook. Answer
- Complete “Check Your Understanding” questions 2, 3, 6.a., 6.b., and 7 on pages 38 to 40 of the textbook. Answer
1.4. Explore 3
Module 1: Function Transformations
Make sure a function is written in the form ![]() or
or ![]() before trying to interpret the function. When a function is written in a different form, such as
before trying to interpret the function. When a function is written in a different form, such as ![]() or
or ![]() , the parameters will behave differently because a different order of operations is implied. The following table shows some examples of different possibilities. Can you think of other examples?
, the parameters will behave differently because a different order of operations is implied. The following table shows some examples of different possibilities. Can you think of other examples?
| Function | Order of Operations Applied to y = f(x) | Used in This Course |
| a and b then h and k | used in this course | |
| a and b then h and k | used in this course | |
| a then h then b then k | not explicitly used in this course | |
| b then k then a then h | not explicitly used in this course | |
| h and k then a and b | not explicitly used in this course |
Order of Transformations illustrates the difference between ![]() and
and ![]() The second function is obtained if you translate before stretching and reflecting.
The second function is obtained if you translate before stretching and reflecting.
As you can see, ![]() and
and ![]() act very differently. This course focuses on the forms
act very differently. This course focuses on the forms ![]() and
and ![]()
As in previous lessons, the process of sketching a function of the form ![]() from y = f(x) can be reversed to determine an equation given the graph of f(x) and an image of the graph. The next two examples describe this process.
from y = f(x) can be reversed to determine an equation given the graph of f(x) and an image of the graph. The next two examples describe this process.
Watch Determining an Equation from a Graph.
Read “Example 3” on page 37 of the textbook. This example illustrates how to determine the equation of a function by looking at how individual points are mapped.
Self-Check 3
- Complete “Your Turn” from “Example 3” on page 38 of the textbook. Answer
- Complete “Check Your Understanding” questions 4.a., 10.a., and 13 on pages 39 and 40 of the textbook. Answer
Add the following formula to your copy of Formula Sheet:
1.5. Connect
Module 1: Function Transformations
Complete the Lesson 4 Assignment that you saved in your course folder at the beginning of this lesson. Show work to support your answers.
![]() Save your responses in your course folder.
Save your responses in your course folder.
Project Connection
There is no Project Connection for this lesson.
1.6. Lesson 4 Summary
Module 1: Function Transformations
Lesson 4 Summary
It is possible to perform multiple transformations on a function. The order in which you apply the transformations is important in determining the resulting function. The form of the equation of the function described in the diagram is commonly used when transforming a function, as the different parameters are easily interpreted. Using this form implies that the function is stretched and reflected before it is translated.
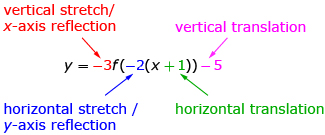
Multiple Transformations reviews how some specific functions of the form ![]() behave when you change the different parameters.
behave when you change the different parameters.

In Lesson 5 you will begin to explore the idea of reversing a function.