Lesson 5
| Site: | MoodleHUB.ca 🍁 |
| Course: | Math 30-1 SS |
| Book: | Lesson 5 |
| Printed by: | Guest user |
| Date: | Tuesday, 9 December 2025, 10:35 PM |
Description
Created by IMSreader
1. Lesson 5
Module 1: Function Transformations
Lesson 5: Inverse of a Relation
Focus

Polka Dot/Thinkstock
Various photo manipulation programs are available that can make editing photos simple and fun. Look at the top sequence of photos and determine the change between each step. Now look at the second series of photos, which was manipulated in the same manner. Suppose you wanted to determine what the original photo looked like. What steps would you have to take? Would the order of these steps be important?

Hemera Technologies/PhotoObjects.net/Thinkstock
Recall that a function is a rule that associates an input with an output. Just as the steps used to modify a photograph can be reversed to determine the original, the instructions given by a function can be reversed—you can use the output of a function to determine the input. The ability to reverse a process is important in many areas of mathematics, and this ability is a key idea in algebra. In Lesson 5 you will investigate how to reverse the output from a function.
Lesson Outcomes
At the end of this lesson you will be able to
- determine the graph of the inverse of f(x) given the graph of f(x)
- determine the equation of the inverse of f(x) given the equation of f(x)
Lesson Question
You will investigate the following question:
- How are a function and its inverse related?
Assessment
Your assessment may be based on a combination of the following tasks:
- completion of the Lesson 5 Assignment (Download the Lesson 5 Assignment and save it in your course folder now.)
- course folder submissions from Try This, and Share activities
- additions to Glossary Terms
- work under Project Connection
Materials and Equipment
- graph paper
1.1. Discover
Module 1: Function Transformations
Discover
Try This 1
Look at the function y = f(x). Recall that y = f(x) can be thought of as a rule relating how y is determined from x. Can you think of a way to express a rule, x = g(y), relating how x can be determined from y? Complete the following questions to explore this idea.
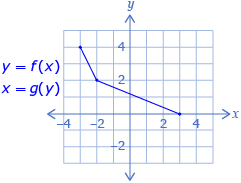
- Use the diagram of y = f(x) to complete a table like the following.

(input, output) for y = f(x) (input, output) for x = g(y) (−3, 4) - Use the (input, output) coordinates from f and g to sketch both on the same coordinate grid. You may use Grid Paper Template to complete this question.
- Determine the domain and range of each relation. How do the domain and range of y = f(x) compare to the domain and range of x = g(y)?

- What visual relationship is there between the graphs of y = f(x) and y = g(x)? Use Reflections and Inverses to determine the line that y = f(x) is reflected across to produce the graph of y = g(x).

![]() Save your work in your course folder.
Save your work in your course folder.
1.2. Explore
Module 1: Function Transformations
Explore
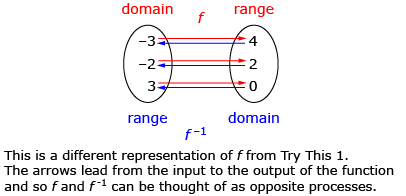
In Try This 1 you saw that the two functions y = f(x) and x = g(y) “undid” each other. An input of −3 into function f gave an output of 4, whereas an input of 4 into function g gave an output of −3. Functions that “undo” each other, such as f and g, are called inverses. The function g(x) is often written as f −1(x).
You may have noticed that the domain and range of the function became the range and domain of the inverse, respectively. This will always be true of inverses.
Watch Function Notation—Explanation to see a graphical representation of the different notations used so far in this lesson.
Note that ![]() If you want the reciprocal of f(x), it can be written
If you want the reciprocal of f(x), it can be written ![]() In this lesson you are studying inverse functions, not reciprocals.
In this lesson you are studying inverse functions, not reciprocals.
As you saw in Try This 1, the inverse of a function can be found by switching the x- and y-coordinates. The original relation and its inverse were both functions in Try This 1. Do you think the inverse of a function will always be a function?
Try This 2
Open Inverse of a Function. This applet shows various functions and their inverses. Try looking at the different functions available in the applet to help you answer the following questions.
- Use the applet to determine when the inverse of a function is a function.
- Describe a rule that could be used on the original function to determine whether or not its inverse will be a function.
![]() Save your responses in your course folder.
Save your responses in your course folder.
1.3. Explore 2
Module 1: Function Transformations
The following example describes how to determine the inverse of a function, the domain and range of both relations, and whether the inverse is a function.
Read “Link the Ideas” and “Example 1” on pages 46 and 47 of the textbook.
In “Example 1” you saw that the inverse of a function may not be a function. When this is the case, function notation is not appropriate—that is, y = f −1(x) may not be an appropriate title for the inverse. In this case, the title “inverse of f(x)” may be used.
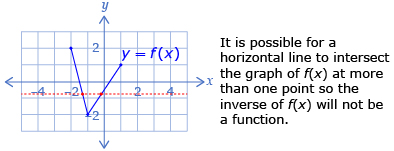
Just as you can check if a relation is a function by using the vertical line test, a horizontal line test can be used to determine if the inverse of a relation is a function. If it is possible for a horizontal line to cross the graph of a relation at more than one point, the inverse will not be a function.
Self-Check 1
![]()
- Complete “Your Turn” from “Example 1” on page 47 of the textbook. Answer
- Complete “Check Your Understanding” question 2 on page 51 of the textbook. Answer
Although the inverse of a function may not be a function, it is often possible to restrict the domain of the function so the inverse is a function. The following example explains how.
Read “Example 2” on page 48 of your textbook.
Self-Check 2
1.4. Explore 3
Module 1: Function Transformations
So far you have looked at the graphs of relations and their inverses. You will now check how to determine the equation of an inverse given the equation of a function.
Try This 3
- Use f(x) = 3x − 4 to complete the following table.
x f(x) −3 −2 −1 0 1 2 3 - Use the data from question 1 to help you complete the following table.
x f −1(x) −3 −2 −1 0 1 2 3 -
Determine an equation of the form f −1(x) =_______ that could be used to represent the table of values in question 2.

- Complete questions 1 to 3 using the function f(x) = 2x2.
- Is the inverse of f(x) = 2x2 a function? Explain.
- Is it reasonable to use the notation f −1(x) for question 3?
![]() Save your work in your course folder.
Save your work in your course folder.
Share 1
With a partner or group, discuss the following questions based on the information from Try This 3.
- How did your equations for question 3 compare?
- How could you have determined the equation in question 3 without making a table of values?
- Why is it difficult to write the inverse of 2x2 using function notation? Is it possible to use function notation for this inverse?
![]() If required, save a record of your discussion in your course folder.
If required, save a record of your discussion in your course folder.
1.5. Explore 4
Module 1: Function Transformations
In Try This 3 you may have found it is possible to determine the equation of an inverse given the equation of a function. One method of doing this procedure is to replace f(x) with y, switch x and y, and solve for y. Then f(x) is replaced with y to avoid equations that contain the variable f(x), which can be confusing. The following example shows how to do this procedure. Take note of when it is appropriate to use function notation to represent an inverse and when it is not appropriate.
Read “Example 3” on pages 49 and 50 of the textbook.
Self-Check 3
- Complete “Your Turn” for “Example 3” on page 50 of your textbook. Answer
- Complete “Check Your Understanding” questions 9.a., 9.d., 15.a., 15.b., and 16 on pages 53 and 54 of the textbook. Answer
Add the following terms to your copy of Glossary Terms:
- inverse
- horizontal line test
1.6. Connect
Module 1: Function Transformations
Complete the Lesson 5 Assignment that you saved in your course folder at the beginning of this lesson. Show work to support your answers.
![]() Save your responses in your course folder.
Save your responses in your course folder.
Project Connection
Complete Module 1 Project: Designing with Transformations.
![]() Save your responses in your course folder.
Save your responses in your course folder.
Submit your completed Module 1 Project to your teacher.
1.7. Lesson 5 Summary
Module 1: Function Transformations
Lesson 5 Summary
If relations f and g undo each other, they are called inverses. If f and g are both functions, g is often written as f −1. You have seen that the domain and range of the function become the range and domain of the inverse, respectively. This will always be true of inverses.
To determine an inverse graphically, switch the x- and y-coordinates of each point of the original graph to determine points of the inverse. The inverse of a function may or may not be a function. Just as you can check if a relation is a function by using the vertical line test, a horizontal line test can be used on the original graph to determine if the inverse of that relation will be a function. If it is possible for a horizontal line to cross the graph of a relation at more than one point, the inverse will not be a function.
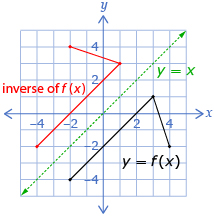
This diagram shows y = f(x) and its inverse. The inverse is not labelled y = f −1(x) because the inverse is not a function.
You have also found that it is possible to determine the equation of an inverse given the equation of a function. One method used is to replace f(x) with y, switch x and y, and then solve for y. Then f(x) is replaced with y to avoid equations that contain the variable f(x), which can be confusing. Take note of when it is appropriate to use function notation to represent an inverse and when it is not appropriate.
Although this is the end of the transformations module, many of these ideas will recur throughout the course. In Module 2 you will focus on radical functions.