Lesson 4
| Site: | MoodleHUB.ca 🍁 |
| Course: | Math 30-1 SS |
| Book: | Lesson 4 |
| Printed by: | Guest user |
| Date: | Tuesday, 9 December 2025, 10:34 PM |
Description
Created by IMSreader
1. Lesson 4
Module 4: Foundations of Trigonometry
Lesson 4: Trigonometric Ratios
Focus
Stockbyte/Thinkstock
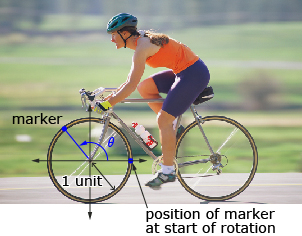
Cycling is a great part of a healthy lifestyle and also contributes to a greener environment. Physical activity relieves stress by producing a balance between exertion and relaxation. The cyclical movement of the legs stimulates muscles in the lower back to strengthen the spine. The uniform, cyclical movement of cycling creates a considerable relaxing effect, which stabilizes the physical and emotional functions of the body.
Take a closer look at this cyclical motion.
As you saw in Lesson 3, when choosing a radius of one unit for the wheel, the circumference of the wheel is 2π. When the outer edge of the wheel has travelled 2π, the wheel has gone through exactly one revolution, and so is back where it started. Thus, if a marker was placed on the wheel, you could look at the height and angle of rotation of the marker at specific times and relate these measures to points on the unit circle.
In Lesson 3 you derived the equation for the unit circle, and you determined the rotational angles in standard position and the coordinates of points where a terminal arm intersects the unit circle for specific angles.
In this Lesson you will discover how the unit circle can be related to trigonometric ratios.
Lesson Outcomes
At the end of this lesson you will be able to
- describe the six trigonometric ratios
- determine the exact value of trigonometric ratios for specific angles
- determine the approximate value of trigonometric ratios of any angle
Lesson Question
You will investigate the following question:
- How can the six trigonometric ratios be determined for any angle expressed in radians or degrees?
Assessment
Your assessment may be based on a combination of the following tasks:
- completion of the Lesson 4 Assignment (Download the Lesson 4 Assignment and save it in your course folder now.)
- course folder submissions from Try This and Share activities
- additions to Glossary Terms and Formula Sheet
- work under Project Connection
1.1. Launch
Module 4: Foundations of Trigonometry
Launch
Do you have the background knowledge and skills you need to complete this lesson successfully? Launch will help you find out.
Before beginning this lesson, you should be able to
- determine in each quadrant if the trigonometric ratios are positive or negative
- determine the trigonometric ratios for an angle in standard position given a point on a terminal arm
- determine the approximate value of a trigonometric ratio given an angle in degrees
1.2. Are You Ready?
Module 4: Foundations of Trigonometry
Are You Ready?
Complete these questions. If you experience difficulty and need help, visit Refresher or contact your teacher.
- Determine in which quadrant(s) the terminal arm would lie for the given values of θ.
- Point A(2, −3) lies on the terminal arm of angle θ in standard position. Determine the exact trigonometric ratios for sin θ, cos θ, and tan θ. Answers
- Determine the approximate value of each trigonometric ratio to the nearest hundredth.
- Determine the exact values of each trigonometric ratio.
If you answered the Are You Ready? questions without problems, move to Discover.
If you found the Are You Ready? questions difficult, complete Refresher.
1.3. Refresher
Module 4: Foundations of Trigonometry
Refresher
Review in which quadrants the trigonometric ratios are positive or negative and the CAST rule in Trigonometric Ratios in All Four Quadrants.
The CAST Rule can be used to help remember signs of the different ratios for each quadrant. This rule is based on the signs of the coordinates in each quadrant.
Review Finding Angles from a Point on the Terminal Arm. This example outlines how to determine trigonometric ratios given a point on a terminal arm.
Review Formal Definitions for Primary Trigonometric Ratios. This outlines how to express trigonometric ratios in terms of x, y, and r.
Watch Using a 30-60-90 Triangle for a 150° Angle. This example outlines how to determine the exact value of a trigonometric ratio using reference triangles.
Watch Using a 30-60-90 Triangle for a 300° Angle. This example outlines how to determine the exact value of a trigonometric ratio using reference triangles.
Go back to the Are You Ready? section and try the questions again. If you are still having difficulty, contact your teacher.
1.4. Discover
Module 4: Foundations of Trigonometry
Discover
Try This 1
Use Investigating Trigonometric Ratios and the Unit Circle to answer these questions. Use the angle θ slider to see how the x- and y-coordinates of point P on the unit circle relate to cos θ, sin θ, and tan θ.
- Choose two points in each quadrant. Fill in a chart similar to the following for each point you choose. Add more rows as needed.
Angle θ Point (x, y) Quadrant x y cos θ sin θ tan θ
(as a fraction)tan θ 45° (0.7071, 0.7071) 1 0.7071 0.7071 0.7071 0.7071 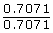
1
- What relationship do you see between the values of x, y, cos θ, sin θ, and tan θ?
![]() Save your responses in your course folder.
Save your responses in your course folder.
Share 1
With a partner or group, explain why you think the relationships you observed in Try This 1 exist between the values of x, y, cos θ, sin θ, and tan θ.
![]() If required, place a summary of your discussion in your course folder.
If required, place a summary of your discussion in your course folder.
1.5. Explore
Module 4: Foundations of Trigonometry
Explore
In Try This 1 you may have noticed the following relationships:
- cos θ = x
- sin θ = y
Are these relationships only valid for points on a unit circle? In Try This 2 you will explore these relationships further in order to help answer this question.
Try This 2
Use Trigonometric Ratios and the Unit Circle to answer the following questions. You can change theta by using the angle slider.

- Write an expression for cos θ in terms of the line segments of the triangle—OA, OP, or AP. You may want to click the Hint checkbox in the applet.
- Write an expression for sin θ in terms of the line segments of the triangle—OA, OP, or AP.
- Write an expression for tan θ in terms of the line segments of the triangle—OA, OP, or AP.
- What is the length of line segment OP, since this is the unit circle? Replace line segment OP with this value in your previous answers.
- The length of OA is the same value as the x-coordinate of point P, and the length of AP is the same value as the y-coordinate of point P. Replace OA and AP with x and y in your expressions from question 4.
- Use your answers from question 5 to write expressions for the coordinates of point P.
- Would the expressions in question 6 be different for a point on a circle when the radius is not 1? Why or why not?
![]() Save your responses in your course folder.
Save your responses in your course folder.
1.6. Explore 2
Module 4: Foundations of Trigonometry
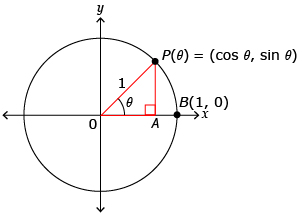
In Try This 2 you found the following is true for a point P(x, y) on the unit circle:
This information can be simplified to the following:
| cos θ = x | sin θ = y |
Source: Pre-Calculus 12. Whitby, ON: McGraw-Hill Ryerson, 2011.
Reproduced with permission.
So, you can write any point that lies on the unit circle at angle θ as P(θ) = (x, y) or P(θ) = (cos θ, sin θ).
Now that the relationship between a point P(x, y) and cos θ, sin θ, and tan θ has been identified, you can use this information to solve problems. An example of how to use the coordinates of a point on the unit circle to determine trigonometric ratios for an unknown angle follows.
Example: Determining Trigonometric Ratios Using a Point on the Unit Circle
The point P![]() lies on the unit circle at the intersection of a terminal arm of angle θ in standard position. Determine the values of sin θ, cos θ, and tan θ leaving the ratios as fractions.
lies on the unit circle at the intersection of a terminal arm of angle θ in standard position. Determine the values of sin θ, cos θ, and tan θ leaving the ratios as fractions.
Solution
Draw a diagram.
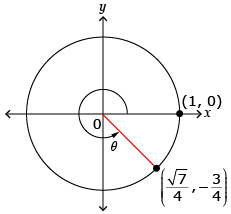
Point P is on the unit circle.
Determine cos θ. Since point P is on the unit circle, cos θ = x. The x-coordinate is, therefore, equal to cos θ.
![]()
Determine sin θ. Since point P is on the unit circle, sin θ = y. The y-coordinate is, therefore, equal to sin θ.
![]()
Determine tan θ.
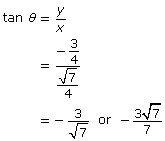
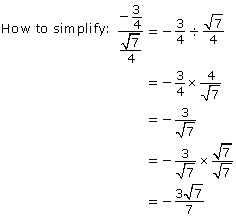
Self-Check 1
The point P![]() lies on the unit circle at the intersection of a terminal arm of angle θ in standard position.
lies on the unit circle at the intersection of a terminal arm of angle θ in standard position.
- Sketch a diagram of point P on the unit circle, and label angle θ in standard position. Answers
- Determine the values of sin θ, cos θ, and tan θ. Leave the ratios as fractions. Answers
1.7. Explore 3
Module 4: Foundations of Trigonometry
In previous mathematics courses you learned the three trigonometric ratios of sine, cosine, and tangent.
Three other trigonometric ratios are used in mathematics: cosecant, secant, and cotangent. They are the reciprocals of sine, cosine, and tangent.
![]()
![]()
![]()
Just as there are abbreviations for sine, cosine, and tangent, there are abbreviations for the reciprocal trigonometric ratios.
![]()
![]()
Read “Example 1” on page 193 of the textbook. Note the following while reading.
- cos θ and sin θ are the x- and y-coordinates of point A.
- To find tan θ, divide the two coordinates,
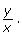
- csc θ, sec θ, and cot θ are the reciprocal ratios, so take the reciprocal of sin θ, cos θ, and tan θ to find these ratios.
Self-Check 2
Determine the three reciprocal ratios for point P![]() on the unit circle.
on the unit circle. ![]() Answers
Answers
1.8. Explore 4
Module 4: Foundations of Trigonometry
Read “Example 5” on page 200 in the textbook. Note the following while reading.
- The coordinates of point A are the values of x and y on the triangle.
- To determine r, use the Pythagorean theorem to solve
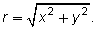
- The radius, r, is always positive because it is a length without a direction.
- There are six trigonometric ratios you have to determine.
Self-Check 3
- The point A(−3, −2) lies on the terminal arm of an angle θ in standard position. Determine the values of csc θ and sec θ. Leave your answer as a fraction. Explain your process.
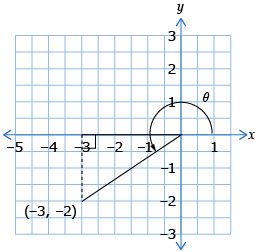
Answer - Determine the value of cot θ when
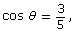 where
where 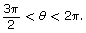 Sketch a diagram to help determine the exact value. Leave your answer as a fraction.
Sketch a diagram to help determine the exact value. Leave your answer as a fraction.  Answer
Answer
![]()
- Complete question 12.b. on page 202 in the textbook. Answer
You have looked at finding trigonometric ratios when given a point on the terminal arm of an angle in standard position. How can you determine trigonometric ratios when only given an angle?
In Mathematics 20-1 you used reference triangles of 30°-60°-90° or 45°-45°-90° to help determine the exact values for trigonometric ratios for multiples of these angles. The unit circle can assist you in determining the exact values for trigonometric ratios as well. You will determine six different trigonometric ratios for angles measured in degrees and radians.
1.9. Explore 5
Module 4: Foundations of Trigonometry
Try This 3
In Try This 3 you will determine the exact value for ![]()
- Draw a diagram of the angle
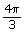 in standard position.
in standard position. - Choose either Part A or Part B to determine the exact value.
Part A: Look up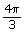 on the unit circle from Lesson 3.
on the unit circle from Lesson 3. 
Part B: Determine the angle from the terminal arm to the x-axis; then choose one of the reference triangles to help determine the exact value.
-
Write the exact value for
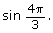
![]() Save your responses in your course folder.
Save your responses in your course folder.
Share 2
With a partner or group, discuss the strategy you used in Try This 3. Explain any similarities or differences in your strategies, and describe which strategy you prefer and why.
![]() If required, save a record of your discussion in your course folder.
If required, save a record of your discussion in your course folder.
A term that you will use is reference angle, θR. This angle is the acute, positive angle between the x-axis and the terminal arm.
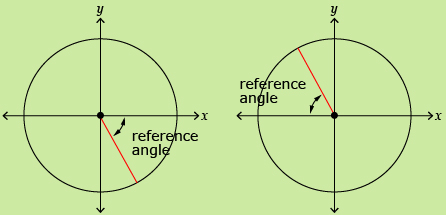
Remember to look at which quadrant ![]() is in to determine whether the value is positive or negative.
is in to determine whether the value is positive or negative.
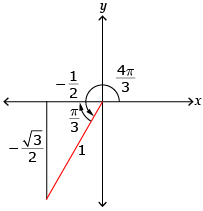
1.10. Explore 6
Module 4: Foundations of Trigonometry
In Try This 3 you determined the exact value for ![]() You may have used the unit circle, reference triangles, or some other process to determine the value of the trigonometric ratio. Determining Exact Values for Trigonometric Ratios will demonstrate using the unit circle or reference triangles to determine the exact values for trigonometric ratios.
You may have used the unit circle, reference triangles, or some other process to determine the value of the trigonometric ratio. Determining Exact Values for Trigonometric Ratios will demonstrate using the unit circle or reference triangles to determine the exact values for trigonometric ratios.
Watch Determining Exact Values for Trigonometric Ratios to see how to determine the exact value of sec ![]()
Self-Check 4
![]()
- Complete “Your Turn” at the bottom of page 195 in the textbook. Answers
- Complete questions 1.c., 1.e., and 1.g. on page 201 in the textbook. Answers

iStockphoto/Thinkstock
You can calculate approximate values for trigonometric ratios by using your calculator.
Your calculator can determine the trigonometric values for angles measured in degrees or radians. You will need to choose the correct mode for your calculator. Check your calculator manual to change from degree to radian mode and back again. For example:
- To calculate sin 75°, you would use degree mode. So, sin 75° = 0.965 925 826…
- To calculate
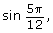 you would use radian mode. So,
you would use radian mode. So, 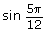 = 0.965 925 826…
= 0.965 925 826…
Most calculators do not have cosecant, secant, or cotangent buttons. You can still calculate the value of these ratios by using your calculator.
Example
Determine the approximate value of sec (−4.1), and round your answer to four decimal places.
Solution
For this question, your calculator should be in radian mode since −4.1 is a radian measure. Remember, when there is no degree symbol, assume the angle is measured in radians.
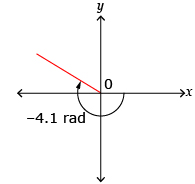
In which quadrant would the angle −4.1 terminate?
The angle terminates in quadrant 2. The value of the cosine ratio is negative in quadrant 2 because the value of the x-coordinate is negative in quadrant 2. If the cosine ratio is negative, the value of the secant ratio will also be negative.
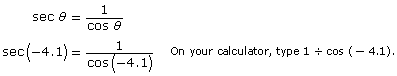
![]()
If you did not get this answer, check to see if your calculator is in radian mode.
Self-Check 5
![]()
- Complete questions 2.c., 2.g., and 2.j. on page 201 in the textbook. Answers
- Complete question C1 on page 204 in the textbook. Answers
Add the following terms to your copy of Glossary Terms:
- cosecant
- secant
- cotangent
Add the following formulas to your copy of Formula Sheet:
1.11. Connect
Module 4: Foundations of Trigonometry
Complete the Lesson 4 Assignment that you saved in your course folder at the beginning of this lesson.
![]() Save your responses in your course folder.
Save your responses in your course folder.
Project Connection
You should now be prepared to complete the next step in your project. Go to Module 4 Project: The Ferris Wheel. Complete Part 1: Activity 3.
![]() Save all your responses in your course folder.
Save all your responses in your course folder.
1.12. Lesson 4 Summary
Module 4: Foundations of Trigonometry
Lesson 4 Summary
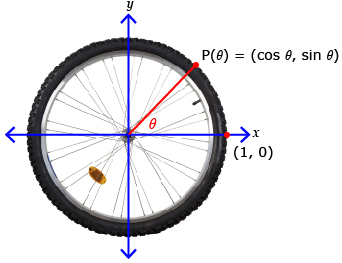
In this lesson you started with points on the unit circle. At the beginning of the lesson, a reference was made to a bicycle tire rotating though an angle θ with a marker on the tire and a radius of 1 unit. The coordinates of the marker would equal the cosine and sine ratio for the angle θ. Points where the terminal arm of angle θ and the unit circle intersect can be defined as P(θ) = (cos θ, sin θ).
Three reciprocal trigonometric ratios are used in this course.
This means if ![]() then
then
You can use P(θ) = (cos θ, sin θ) to help determine the six trigonometric ratios. So, cos θ = x-coordinate, sin θ = y-coordinate, and ![]() or
or ![]()
iStockphoto/Thinkstock
To determine the trigonometric ratios for a point not on the unit circle, use the coordinates x and y and determine r. When given an angle, you can determine the exact values for trigonometric ratios using the unit circle or reference angles. Your calculator can determine approximate values for trigonometric ratios in the correct mode.
For a summary on the unit circle, you may choose to watch the video Unit Circle Definition of Trig Functions.