Lesson 4
| Site: | MoodleHUB.ca 🍁 |
| Course: | Math 30-1 SS |
| Book: | Lesson 4 |
| Printed by: | Guest user |
| Date: | Tuesday, 9 September 2025, 2:15 AM |
Description
Created by IMSreader
1. Lesson 4
Module 5: Trigonometry Applications and Identities
Lesson 4: Using Identities to Solve Equations
Focus
Comstock/Jupiterimages/Thinkstock
A mechanic is planning to fix a car. She has taken down a set of imperial wrenches, but finds all the bolts on the car are metric and her wrenches don’t fit properly. What should she do? Clearly, she should switch the imperial wrenches for a metric set so they are useable.
iStockphoto/Thinkstock
The halves of an identity can be thought of as the two wrench sets; each part is useful at different times. To use an identity, you can switch one half of the identity for the other to make an expression easier to work with.
Lesson Outcomes
At the end of this lesson you will be able to
- simplify expressions using trigonometric identities
- solve equations using trigonometric identities
Lesson Question
You will investigate the following question:
- How can trigonometric identities be used to solve problems?
Assessment
Your assessment may be based on a combination of the following tasks:
- completion of the Lesson 4 Assignment (Download the Lesson 4 Assignment and save it in your course folder now.)
- course folder submissions from Try This and Share activities
- additions to Glossary Terms and Formula Sheet
- work under Project Connection
1.1. Discover
Module 5: Trigonometry Applications and Identities
Discover
Try This 1
Open Sum Identity, which shows a rectangle ABCD, where BC < 2AB. E is a point on BC and F is a point on CD such that ∠AEF is a right angle. ∠BAE has been labelled α (alpha) and ∠EAF has been labelled β (beta).
- Set point E to a position you like and sketch the diagram on a full piece of paper. Use the measures of α and β to determine the rest of the angles in the diagram.
Click the “Show angles” box in Sum Identity to check your values. -
- Explain how you know ∠CEF = α.
-
Determine an expression for each of the acute angles in the diagram in terms of α and β. Label each angle in your diagram.
-
The hypotenuse AF of the inscribed right triangle has a length of 1 unit. Explain why the length of AE can be represented as cos β. Label AE as cos β.
- Determine an expression for line segment AB in terms of sin α, cos α, sin β, and cos β. (You will not need all of these.) Write this expression on your diagram.
Click the “Show AE and AB lengths” box in Sum Identity to check your expression. - Determine expressions for BE, EF, CE, CF, AD, and DF in terms of sin α, cos α, sin β, and cos β. Label each side length on your diagram using these sines and cosines.
Click the “Show all lengths” box to check your diagram. -
-
Which angle in the diagram, other than ∠BAF, is equal to α + β?
-
AD = BE + EC. Use this fact to determine a trigonometric identity that relates the two side lengths.
- Predict another identity using the fact that AB = DC.
-
Save your answers in your course folder.
Share 1
With a partner or group, discuss the following questions based on your responses to Try This 1.
- Verify your possible identities from parts 6.b. and 6.c. numerically using values of α and β.
- Does each identity apply to angles that are obtuse? Are there any restrictions on the domain? Describe your findings.
If required, save a record of your discussion in your course folder.
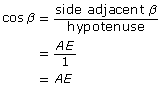
1.2. Explore
Module 5: Trigonometry Applications and Identities
Explore
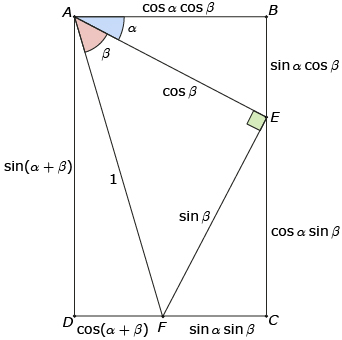
In Try This 1 you may have drawn a diagram similar to the diagram shown here.
By recognizing that AD = BE + CE, you can predict the identity sin (α + β) = sin α cos β + cos α sin β. Similarly, because AB = DF + CF, cos α cos β = sin α sin β + cos (α + β). This second identity is often rewritten as cos (α + β) = cos α cos β − sin α sin β. These two identities are called sum identities. In Try This 2 you will use the sum identities to predict other identities.
Try This 2
- Explain why sin (−x) = −sin x and cos (−x) = cos x are identities.
-
Use the sum identity sin (A + B) = sin A cos B + cos A sin B, and the identities from question 1 to show that sin (A − B) = sin A cos B − cos A sin B.
- Using a procedure similar to that of question 2, predict an identity for cos (A − B).
-
Consider the special case where A = B for the identities sin (A + B) = sin A cos B + cos A sin B and cos (A + B) = cos A cos B − sin A sin B. Write simplified equivalent expressions for sin 2A and cos 2A.
Save your answers in your course folder.
Two possible identities are
For the cosine sum, begin with
For the sine sum, begin with
Replacing every B with −B still makes the identity true.
1.3. Explore 2
Module 5: Trigonometry Applications and Identities
In Try This 2 you determined a number of different identities. These are summarized in the following tables. The tables also include sum and difference identities for tangent and three different versions of the double-angle identity for cosine.
| Sum Identities | Difference Identities |
| sin (A + B) = sin A cos B + cos A sin B | sin (A − B) = sin A cos B − cos A sin B |
| cos (A + B) = cos A cos B − sin A sin B | cos (A − B) = cos A cos B + sin A sin B |
 |
 |
| Double-Angle Identities | |
| sin 2A = 2 sin A cos A | cos 2A = cos2 A − sin2 A |
 |
cos 2A = 2 cos2 A − 1 |
| cos 2A = 1 − 2 sin2 A |
Read “Example 1” on page 301 of your textbook to see an example of how some of these identities can be used to simplify expressions.
Self-Check 1
Complete questions 1.a., 1.c., 1.e., 2.a., and 2.c. on page 306 of the textbook. Answer
So far you have seen that identities are statements that are always true when they are defined. Identities are useful in changing the form of an expression by substituting one side of the identity for the other. The following example shows how this can be done.
Read “Example 3” on pages 302 and 303 of the textbook. Pay attention when identity substitutions are used. For part a., notice that it is also possible to determine non-permissible values by solving sin 2x = 0 for x.
Self-Check 2
- Complete “Your Turn” from “Example 3” on page 303 of the textbook. Answer
- Complete questions 4.b., 4.d., 5.a., 5.d., and 12 on pages 306 to 307 of the textbook. Answer
It is possible to use the identities learned so far in this lesson to determine the exact value for some trigonometric expressions that use angles that are not multiples of 30°, 45°, or 60°. Complete Try This 3 to see how.
Try This 3
Consider the expression cos 75°.
- Write 75° as a sum or difference of angles that are multiples of 30°, 45°, or 60°.
- Use an identity to rewrite cos 75° in terms of the sum or difference you determined in question 1.
- Determine the exact value of your new expression. This is the exact value of cos 75°.
- Use a calculator to approximate cos = 75° and to approximate the exact value you determined in question 3. Do you get the same value?
Save your responses in your course folder.
Share 2
With a partner or group, discuss the following question based on your solution to Try This 3.
Could you have rewritten 75° differently than you did in Try This 3 to determine the value of cos 75°? Explain.
If required, save a record of your discussion in your course folder.
1.4. Explore 3
Module 5: Trigonometry Applications and Identities
Self-Check 3
- Complete the activity in “Sum and Difference Identities for Sine and Cosine.”
Screenshot reprinted with permission of ExploreLearning
- Complete questions 7, 8.b., 8.c., 10, 20.b., and 20.c. on pages 306 and 307 of the textbook. Answer
So far you have used identities to simplify expressions. Sometimes a trigonometric identity can be useful when solving an equation. Try This 4 illustrates this.
Try This 4
Consider the equation 
.
- Why is this equation difficult to solve algebraically in its current form?
- Which identity will allow you to convert cos2 x to an expression that only uses sines?
- Convert the equation to only sines and solve the equation for the domain 0 ≤ x < 2π.
- Substitute the solution you found in question 3 back into the original equation. Does the result make sense? Explain.
Save your responses in your course folder.
Share 3
With a partner or group, discuss the following questions based on the information from Try This 4.
- Why was it necessary to rewrite the equation so it only had one trigonometric function?
- Why is it easier to convert cos2 x to sines than sin x to cosines for this problem?
If required, save a record of your discussion in your course folder.1.5. Explore 4
Module 5: Trigonometry Applications and Identities
In Try This 4 you may have noticed that using the Pythagorean identity, sin2 x + cos2 x = 1, allows you to rewrite 
This equation now contains only sines and can be solved using a factoring strategy you learned in Module 4. A complete solution to this problem is shown.
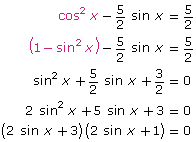
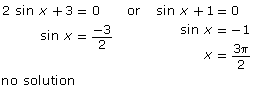
Solving Equations Using Identities shows how an equation can be solved with the help of a double-angle identity.
When solving an equation using an identity, it is important to check for non-permissible values in the original equation. If a non-permissible value shows up as a solution, the value cannot be included.
Self-Check 4
1.6. Explore 5
Module 5: Trigonometry Applications and Identities
Add the following terms to your copy of Glossary Terms:
- sum identity
- difference identity
- double-angle identity
Add the following identities to your copy of Formula Sheet:
- sin (A + B) = sin A cos B + cos A sin B
- cos (A + B) = cos A cos B − sin A sin B
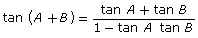
- sin (A − B) = sin A cos B − cos A sin B
- cos (A − B) = cos A cos B + sin A sin B
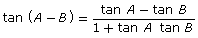
- sin 2A = 2 sin A cos A
- cos 2A = cos2 A − sin2 A
- cos 2A = 2 cos2 A − 1
- cos 2A = 1 − 2 sin2 A
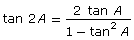
1.7. Connect
Module 5: Trigonometry Applications and Identities
Complete the Lesson 4 Assignment that you saved in your course folder at the beginning of this lesson. Show work to support your answers.
Save your responses in your course folder.
Project Connection
You are now ready to apply your understanding of how trigonometric identities can be used to solve equations. Go to Module 5 Project: Pushing the Limits of Vehicle Performance. Complete Activity 1: Part 2.
Save your responses in your course folder.
Going Beyond
Prosthaphaeresis
Before logarithms were used, and much before pocket calculators were invented, product identities were used to estimate the value of products. An example of a product identity is 
The process is called prosthaphaeresis and can be thought of in four steps:
- Scale down by moving the decimal place of each value so it is between 0 and 1.
- Use cos−1 on each value to determine an A and B value. (Historically this would have been done with a table of cosine values.)
- Use the identity to determine the product.
- Scale up by moving the decimal place to the right (or left) as many places as you moved it to the left (or right) for each input.
Consider 127 × 588.
Step 1: 0.127 × 0.588
Step 2: = cos (1.4434…) cos (0.9422…)
Step 3: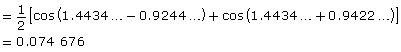 
Step 4: 74 606
So, 127 × 588 = 74 606.
1.8. Lesson 4 Summary
Module 5: Trigonometry Applications and Identities
Lesson 4 Summary
There is no limit to the number of possible trigonometric identities. In this lesson you focused on a set of related identities: the sum, difference, and double-angle identities. You also saw that it is often possible to predict an identity from previous knowledge.
Sum Identities |
Difference Identities |
sin (A + B) = sin A cos B + cos A sin B |
sin (A − B) = sin A cos B − cos A sin B |
cos (A + B) = cos A cos B − sin A sin B |
cos (A − B) = cos A cos B + sin A sin B |
|
|
Double-Angle Identities |
|
sin 2A = 2 sin A cos A |
cos 2A = cos2A − sin2A |
|
cos 2A = 2 cos2A − 1 |
|
cos 2A = 1 − 2 sin2A |
Identities are useful when you are interested in changing the form of an equation or expression; you simply exchange one side of the identity for the other. Remember, if your identity has a restricted domain, that restriction will carry on to the equation or expression if the identity is used.
In the next lesson you will learn how to prove a trigonometric identity and, more importantly, why you would want to do that.