Lesson 3
| Site: | MoodleHUB.ca 🍁 |
| Course: | Math 30-1 SS |
| Book: | Lesson 3 |
| Printed by: | Guest user |
| Date: | Tuesday, 9 December 2025, 10:35 PM |
Description
Created by IMSreader
1. Lesson 3
Module 6: Exponents and Logarithms
Lesson 3: Understanding Logarithms
Focus

iStockphoto/Thinkstock
In the early 1600s, John Napier published a way to reduce the tedious process of multiplying large numbers to the easier process of addition. His process involved looking up numbers (which he called logarithms) in a table of values. It took Napier 20 years to create that table of values!
At the time, Napier’s process was very useful to astronomers who needed to multiply large numbers together. Today, however, logarithms are not used for multiplying large numbers; calculators are used instead. That said, there are other uses of logarithms. You will use logarithms in future lessons to solve exponential equations. Before you can solve exponential equations in this new way, you need to explore the concept of logarithms.

iStockphoto/Thinkstock
In Lesson 1 you studied exponential functions and how they can be used to describe growth or decay. In this lesson you will be introduced to logarithmic functions. These functions can also be used to describe growth or decay. The growth of a tree can be modelled using a logarithmic function. The height of the tree starts with a rapid increase and then the growth rate slows.
Lesson Outcomes
At the end of this lesson you will be able to
- explain the relationship between logarithms and exponents
- express a logarithmic expression as an exponential expression and vice versa
- determine the value of a logarithm
Lesson Question
You will investigate the following question:
- What are logarithms and how is the value of a logarithm determined?
Assessment
Your assessment may be based on a combination of the following tasks:
- completion of the Lesson 3 Assignment (Download the Lesson 3 Assignment and save it in your course folder now.)
- course folder submissions from Try This and Share activities
- additions to Glossary Terms and Formula Sheet
1.1. Discover
Module 6: Exponents and Logarithms
Discover
In the previous lesson you solved exponential equations by guessing and checking or, when possible, ensuring common bases and then equating the exponents. You verified the solution through graphing or substitution. You will use these same skills to understand logarithms and their uses.
Try This 1
-
- Complete the table provided for the function y = 2x; then graph the function.
x
y
−1
0
1
2
3
4
- State the domain, range, x-intercept, y-intercept, and equation of asymptotes for the graph.
- Complete the table provided for the function y = 2x; then graph the function.
-
- Complete the table provided for the inverse function x = 2y; then graph the inverse function.
x
y
−1
0
1
2
3
4
- State the domain, range, x-intercept, y-intercept, and equation of asymptotes for this inverse relation.
- Complete the table provided for the inverse function x = 2y; then graph the inverse function.
- Does the inverse graph represent a function? Explain your answer.
-
- How many 2’s are multiplied together to produce 8? In other words, 2 to what exponent would equal 8?
- Looking at the inverse function table or graph, when x = 8 what is the y-value?
- What do you notice about your answer to question 4 parts a and b? Why do you think this is?
![]() Save your responses in your course folder.
Save your responses in your course folder.
Share 1
With a partner or group, discuss the following question based on your graph created in Try This 1:
How are the graphs of y = 2x and the inverse, x = 2y, related?
![]() If required, save a record of your discussion in your course folder.
If required, save a record of your discussion in your course folder.
1.2. Explore
Module 6: Exponents and Logarithms
Explore
Your graphs, from Try This 1, of y = 2x and its inverse, x = 2y, may have looked similar to the graphs shown here. The inverse is a function because there is only one x-value for each y-value.
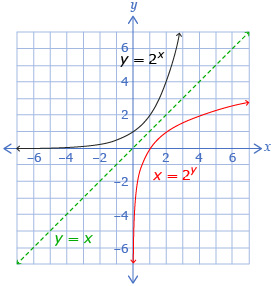
A logarithmic function is the inverse of an exponential function. This means that a logarithmic function is a reflection of the corresponding exponential function in the line y = x.
If you take the inverse function, x = 2y, and let x = 8, the function becomes 8 = 2y. This equation can be described in words as “2 to what exponent equals 8?” Instead of writing it this way, a logarithm could be used to describe the exponent. A logarithm is really the exponent that is required to write a value as a power with a specific base.
When you took the inverse of y = 2x, you produced the function x = 2y. If you were to try to isolate the y-value of x = 2y, you would likely get stuck. Logarithms can help isolate y.
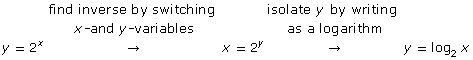
In Lesson 1 you learned that an exponential function is a function in the form y = cx, where c > 0, c ≠ 1. The inverse of the exponential function y = cx would be the logarithmic function in the form y = logc x, where c > 0, c ≠ 1. Logc x is pronounced as “log base c of x”; and log2 x is pronounced as “log base 2 of x.”
In Try This 1 you may have stated the following characteristics about the inverse of the exponential function, the logarithmic function:
- The domain is {x|x > 0, x ∈ R}.
- The range is {y|y ∈ R}.
- The x-intercept is 1.
- There is no y-intercept.
- There is a vertical asymptote at x = 0 (the y-axis).
In the next lesson you will take a closer look at the graphs of logarithmic functions. The rest of this lesson will focus on solving logarithmic expressions.
You have seen how useful the logarithmic form can be to help isolate y in an inverse exponential function. In Try This 2 you will learn more about the logarithmic form and look for patterns between exponential form and logarithmic form.
1.3. Explore 2
Module 6: Exponents and Logarithms
Try This 2
Complete a table like this one.
Initial Value |
Value in Exponential Form |
Value in Logarithmic Form |
1000 |
1000 = 10? |
log10 1000 = ____
|
100 |
100 = 10? |
log10 100 = ____ |
10 000 |
10 000 = 10? |
log10 10 000 = ____ |
81 |
81 = 9? |
log9 81 = ____
|
125 |
125 = 5? |
log5 125 = _____ |
32 |
32 = 2? |
log2 32 = _____ |
![]() Save your responses in your course folder.
Save your responses in your course folder.
Share 2
With a partner or group, discuss the following questions based on Try This 2.
- Describe the patterns you see in Try This 2.
- Summarize your discussion by defining a logarithm or by describing the value of a logarithm.
![]() If required, save a record of your discussion in your course folder.
If required, save a record of your discussion in your course folder.
1.4. Explore 3
Module 6: Exponents and Logarithms
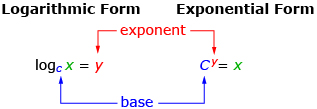
In Try This 2 you may have noticed that the logarithm is equal to the exponent from the exponential form. The relationship between the logarithmic and exponential forms are summarized in the illustration shown.
 1
1
View Evaluating Logarithms for more examples of how to evaluate logarithms. Compare this method of evaluation with your table from Try This 2.
Here is another explanation of logarithms: “Introduction to Logarithms.” However, if you feel confident with logarithms, skip the video and move on to Self-Check 1.
Self-Check 1
![]()
- Complete questions 2.b., 2.d., 3.b., and 4 on page 380 of the textbook. Answer
- Determine the inverse of the function y = 3x.
- Express the following equations in exponential form; then solve for p.
1.5. Explore 4
Module 6: Exponents and Logarithms
Read the summary at the top of page 375 of the textbook. This paragraph summarizes some logarithmic properties. Note how the properties can all be more easily understood by looking at the expression in exponential form.
Try This 3
Now that you have practised evaluating logarithms, it is time to apply this skill to solve logarithmic equations.
- Use your knowledge of logarithms to solve the equation
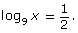
- Express
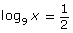 in exponential form.
in exponential form. - Solve for x.

- Express
- Solve the equation logx 49 = 2.
- Express in exponential form.
- Solve for x.

![]() Save your responses in your course folder.
Save your responses in your course folder.
1.6. Explore 5
Module 6: Exponents and Logarithms
In Try This 3 you may have found that ![]() could be changed to exponential form and written as follows:
could be changed to exponential form and written as follows:
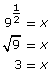
You may have found that logx 49 = 2 could be changed to exponential form and written as follows:
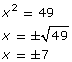
The base of a logarithm is restricted to values greater than zero, so x = −7 is not an acceptable answer. This means x = 7.
If you would like to see more examples of solving expressions involving logarithms, read “Example 2” on page 375 of the textbook.
Self-Check 2
- Complete questions 6, 7, and 12.c. on pages 380 and 381 of the textbook. Answer
- Determine the value of x in the equation
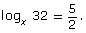 Answer
Answer
Try This 4
You have evaluated logarithms when the answer is a rational number. Not all logarithms will equal a rational number. In this activity you will estimate logarithms for which the value is not a rational number.
Estimate, without using the log functionality of your calculator, the value log2 10 to the nearest tenth. Explain your process. ![]()
![]() Save your responses in your course folder.
Save your responses in your course folder.
1.7. Explore 6
Module 6: Exponents and Logarithms
Read through “Example 4” on page 377 of the textbook. How does the strategy used in “Example 4” to estimate the value of log2 14 compare with the strategy you used in Try This 4?
Self-Check 3
Estimate the value of log3 30 to one decimal place. Explain your answer. Answer

iStockphoto/Thinkstock
Logarithms are helpful in different science applications where logarithmic scales are used. In this activity you will explore the Richter scale, which is a logarithmic scale.
Earthquakes produce seismic waves that are recorded on seismographs. The magnitude of an earthquake is determined from the logarithm of the amplitude of the waves recorded on the seismograph. The Richter scale is used to measure the magnitude of an earthquake. Each whole-number increase in magnitude represents an increase of ten times in measured amplitude of the seismic wave.
Try This 5
The relationship between the amplitude of an earthquake and the Richter scale is defined as ![]() , where
, where
- M is the magnitude on the Richter scale
- A is the amplitude of the earthquake
- A0 is the amplitude of a standard earthquake
Near the east coast of Honshu, Japan, on March 11, 2011, there was a very large earthquake with magnitude 9.0 on the Richter scale. On April 7, 2011, there was an aftershock from the earlier earthquake with magnitude 7.1 on the Richter scale.
- For the initial earthquake, determine how many times greater the amplitude of the earthquake was compared to a standard earthquake, A0.

- Determine how many times greater the amplitude of the seismic wave of the 9.0-magnitude earthquake was compared to the amplitude of the 7.1-magnitude earthquake.

![]() Save your responses in your course folder.
Save your responses in your course folder.

iStockphoto/Thinkstock
The Richter scale was created by American Seismologist Charles F. Richter in 1935. The scale measures the shaking of the ground 100 km from the quake’s epicenter. The Richter scale is a logarithmic scale. So, for each whole-number increase on the scale, the magnitude is increased ten-fold. For example, an earthquake that measures 1.0 on the Richter scale will not even be felt by humans, but a quake that registers 4.0 will cause buildings to shake.
An earthquake that registers 8.0 or higher can be catastrophic. The most powerful earthquake ever recorded occurred in Chile in 1960. This quake had a magnitude of 9.5 on the Richter scale. The 2011 earthquake in Japan registered 9.0 on the Richter scale. This earthquake and the resulting tsunami caused incredible damage and loss of life.

Adapted from: © South Dakota Geological Survey
1.8. Explore 7
Module 6: Exponents and Logarithms
For another example of comparing the magnitude of earthquakes, read “Example 5” on pages 378 and 379 on the textbook. Compare your solution strategies to the ones in “Example 5.” Were the strategies similar?
Self-Check 4
- Complete “Your Turn” at the end of “Example 5” on page 379 of the textbook. Answer
- Complete question 18 on page 381 of the textbook. Answer
- Complete question 16 on page 381 of the textbook. Answer
Add the following terms to your copy of Glossary Terms:
- logarithm
- logarithmic function
Add the following formula to your copy of Formula Sheet:
1.9. Connect
Module 6: Exponents and Logarithms
Complete the Lesson 3 Assignment that you saved in your course folder at the beginning of the lesson. Show work to support your answers.
![]() Save your responses in your course folder.
Save your responses in your course folder.
Project Connection
There is no Project Connection in this lesson.
Going Beyond
Logarithmic equations can be more complicated and have more than one variable. Given two logarithmic equations and two variables, a system of two equations can be used to solve the equations.
Attempt questions 21 and 24 on page 381 of the textbook to see examples of these types of problems.
You can check your answers on page 613 of the textbook.
![]() Save your responses in your course folder.
Save your responses in your course folder.
1.10. Lesson 3 Summary
Module 6: Exponents and Logarithms
Lesson 3 Summary
In this lesson you explored the concept of logarithms. The inverse of an exponential function, y = cx, c > 0, c ≠ 1, is a logarithmic function, y = logc x, c > 0, c ≠ 1. A logarithm of a number is the exponent by which a given base must be raised to produce that number. You can change between exponential and logarithmic forms.
Exponential Form |
Logarithmic Form |
x = cy |
y = logc x |
The logarithmic function is the reflection of the exponential function in the line y = x. The characteristics of the logarithmic function y = logc x, c > 0, c ≠ 1 are as follows:
- The domain is {x|x > 0, x ∈ R}.
- The range is {y|y ∈ R}.
- The x-intercept is 1.
- The vertical asymptote is x = 0, or the y-axis.
In the next lesson you will explore the graphs of different logarithmic functions.

