Lesson 2
| Site: | MoodleHUB.ca 🍁 |
| Course: | Math 30-3 SS |
| Book: | Lesson 2 |
| Printed by: | Guest user |
| Date: | Sunday, 2 November 2025, 5:04 PM |
Description
Created by IMSreader
1. Lesson 2
Module 6: Measurement
Lesson 2: Uncertainty
Focus

Jupiterimages/Comstock/
Thinkstock
Going for a haircut can be a very stressful situation for some people. Their definition of a trim could be very different from their stylist’s definition. Asking for an inch to be cut off could vary in length from very little to a major haircut. The amount of hair that is cut is an estimation by the customer and the stylist. There is uncertainty when people refer to measurements, and uncertainty is connected to the precision of the measurement tool used. Next time you go for a haircut, would you expect your stylist to use a tape measure to help with the cut you’re expecting?
Lesson Outcome
At the end of this lesson you will be able to understand the limitations of measuring instruments relating to precision and uncertainty.
Lesson Questions
You will investigate the following questions:
- How is uncertainty related to precision?
- Why is it important to account for the uncertainty of a measurement?
Assessment
Your assessment may be based on a combination of the following tasks:
- completion of the Lesson 2 Assignment (Download the Lesson 2 Assignment and save it in your course folder now.)
- course folder submissions from Try This and Share activities
- additions to Glossary Terms
- work under Project Connection
1.1. Launch
Module 6: Measurement
Launch
Do you have the background knowledge and skills you need to complete this lesson successfully? Launch will help you find out.
Before beginning this lesson you should be able to add, subtract, multiply, and divide fractions.
1.2. Are You Ready?
Module 6: Measurement
Are You Ready?
Complete these questions. If you experience difficulty and need help, work through Refresher or contact your teacher.
Answer in lowest terms and as a mixed number, if possible.
- Add the following:
- Subtract the following:
- Multiply the following:
- Divide the following:
If you answered the Are You Ready? questions without difficulty, move on to Discover.
If you found the Are You Ready? questions difficult, complete Refresher to review these topics.
1.3. Refresher
Module 6: Measurement
Refresher
For a good review, work through Adding and Subtracting Fractions.
Also work through Multiplying and Dividing Fractions for a good review.
Go back to the Are You Ready? section and try the questions again. If you are still having difficulty, contact your teacher.
1.4. Discover
Module 6: Measurement
Discover
Try This 1
Open the Measurement interactive and choose the bolt to measure.
Create a table similar to the one that follows. Measure the length of the bolt with each of the devices listed in the table. Record the measurement in the table. Compare your measurement to the precision of the measuring device.
Measurement Device |
Precision (cm) |
Measurement (cm) |
Metre Stick |
|
|
Ruler |
|
|
Tape Measure |
|
|
Vernier Caliper |
|
|
![]() Save your responses in your course folder.
Save your responses in your course folder.
Share 1
With a partner or in a group, discuss the following questions related to Try This 1.
- Which measuring device would you choose if you were trying to reproduce the length of the bolt? Explain.
- Which measuring device(s) would you not choose if you were trying to reproduce the length of the bolt? Explain.
![]() If required, place a summary of your discussion in your course folder.
If required, place a summary of your discussion in your course folder.
1.5. Explore
Module 6: Measurement
Explore
Through the Discover activity, you should have found that all measurements are approximate and dependent on the precision of the measuring tool. Look at the following diagram.
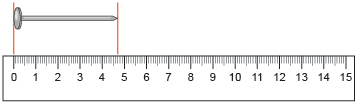
uncertainty: the margin of error of a measurement, if not stated, is half the precision of the measuring device
Source: MathWorks 12 Student Book/Teacher Guide. (Vancouver: Pacific Educational Press, 2011.)
The length of the nail shown is approximately 4.6 cm, meaning it is closer to 4.6 cm than to either 4.5 cm or 4.7 cm. For this reason, it can be said that the length is 4.6 cm, to the nearest tenth of a centimetre. Note that the precision of a measurement is limited by the measuring device. In this case, the precision of the measurement tool is 0.1 cm; therefore, there is some uncertainty in this measurement.
A measured value can be written as follows:
measured value ± measurement uncertainty
Although the precision of the measuring device is 0.1 cm, assume the uncertainty is one-half the precision, or 0.05 cm. Therefore, the measurement can be written as (4.6 ± 0.05) cm.
Try This 2
Use the diagram to answer the following questions.

tennis ball: iStockphoto/Thinkstock
- Measure the diameter of the tennis ball shown using the 15-cm ruler.
- The precision of the ruler is 0.1 cm. State the diameter and the uncertainty.
- Using the uncertainty, what would be the minimum limit of the measurement?

- Using the uncertainty, what is the maximum limit of the measurement?
![]() Save your responses in your course folder.
Save your responses in your course folder.
1.6. Explore 2
Module 6: Measurement
In Try This 2 you probably noticed the following:
- You subtract the uncertainty to get the minimum limit of the measurement.
- You add the uncertainty to get the maximum limit of the measurement.
Now apply this knowledge in Self-Check 1 using an imperial measuring device.
Self-Check 1
Use the picture of the tennis ball to answer the following questions.
Determine the diameter of the tennis ball using an imperial 5-in ruler.

tennis ball: iStockphoto/Thinkstock

iStockphoto/Thinkstock
Precision and uncertainty in measurements occur frequently on the job. The degree of uncertainty tolerated depends upon the type of measurement being taken and the ramifications of an inaccurate measurement.
Over time and after extended use, mechanical parts on equipment wear out and need to be replaced. When a machinist makes a new pin to replace a worn out one, he or she needs to be precise and within an amount of uncertainty to ensure the pin will fit and function properly.
Turn to page 80 of the textbook, and complete “Example 1.” Check your work with the solution that follows on the same page.
Try This 3
Turn to page 81 of the textbook, and complete “Discuss the Ideas” questions 1 to 3.
![]() Save your responses in your course folder.
Save your responses in your course folder.
1.7. Explore 3
Module 6: Measurement

iStockphoto/Thinkstock
In Try This 3 you may have found that tools with different precisions are appropriate for different jobs. Tools with a small precision have a small uncertainty and are good for jobs that require precise measurements. Tools with a larger precision have a larger uncertainty and are good for jobs when approximate measures are acceptable. When considering measurements with uncertainties there are situations, such as when installing flooring, when you need to add or subtract the measurements in order to make the pieces fit together.
Try This 4
- Consider the addition (15 ± 0.5 L) + (24 ± 0.5 L). Describe a method you think may be used to add these two measurements with uncertainties.
To see a method used to add measurements with uncertainties watch Adding Measurements with Uncertainties.
- What is the rule for adding measurements with uncertainties?
- Consider the subtraction (32 ± 0.5 L) − (21 ± 0.5 L). Describe a method you think may be used to subtract these two measurements with uncertainties.
To see a method used to subtract measurements with uncertainties watch Subtracting Measurements with Uncertainties.
- What is the rule for subtracting measurements with uncertainties?
![]() Save your responses in your course folder.
Save your responses in your course folder.
Share 2
With a partner or in a group, share your rules for adding and subtracting measurements with uncertainty.
![]() Save your responses in your course folder.
Save your responses in your course folder.
1.8. Explore 4
Module 6: Measurement
In Try This 4 you saw the following rules:
- You can add measurements with uncertainties by adding the measures and adding the uncertainties.
- You can subtract measurements with uncertainties by subtracting the measures and adding the uncertainties.
Notice that when you subtracted the measures with uncertainties, you still added the uncertainties.
Self-Check 2
- Apply the rules of adding and subtracting measurements to the following.
-
An oilfield hotshot service delivers parts to oilfield rigs and plants in short notice situations. Jim’s Hotshot Service has a one-ton truck with a bumper pull trailer that is used to deliver the parts. Due to cold winter weather and the short notice of work, he plans to build a heated shop that will measure (40.0 ± 0.05) ft to store his truck and trailer in. Jim’s truck measures (21.6 ± 0.05) ft and his trailer measures (18.0 ± 0.05) ft.

Hemera/Thinkstock
You have learned that there are many practical applications that involve minimum and maximum measurements, such as the installation of flooring and determining what can fit in a shop. The ability to calculate the uncertainty in measurements helps to determine whether things can fit together and what the range of measurements could be.
Turn to page 84 of the textbook, and complete “Example 2.” Check your work with the solution that follows on the same page.
1.9. Explore 5
Module 6: Measurement
Whether you are determining the race time for an athlete or determining whether your fridge can fit into a certain space, being able to calculate the uncertainty of measurement is important.
Self-Check 3

Comstock/Thinkstock
A zoo wants to acquire a new animal. However, they must ensure that they can provide the animal with an environment that is as close as possible to its natural environment. For this particular animal, the difference between the highest and lowest temperatures in its natural environment does not exceed 8°C. Several animal houses are available and the zookeeper wants the animal to be as comfortable as possible.
Study the following table regarding four different animal houses; then answer the questions that follow.
Animal House |
Highest Recorded Temperature (°C) |
Lowest Recorded Temperature (°C) |
A |
33.0 ± 0.5 |
22.0 ± 0.5 |
B |
29.0 ± 0.5 |
24.0 ± 0.5 |
C |
25.0 ± 0.5 |
15.0 ± 0.5 |
D |
32.0 ± 0.5 |
25.0 ± 0.5 |
- Are any of the animal houses in the table suitable for the new animal?
- What other factors, beyond temperature range, should be considered for the new animal?
You have learned how to determine the precision of a measuring instrument and how to use this in calculating the uncertainty of a measurement. You have also learned how to add and subtract measurements including their degree of uncertainty. You will now apply this in the following Self-Check.
Self-Check 4
Add uncertainty to your copy of Glossary Terms.
1.10. Connect
Module 6: Measurement
Complete the Lesson 2 Assignment that you saved in your course folder at the beginning of the lesson. Show work to support your answers.
![]() Save your responses in your course folder.
Save your responses in your course folder.
Project Connection
You are now ready to apply your knowledge of measurement and uncertainty to Module 6 Project: Project Measurement. Go to the Module 6 Project, and complete Part 2: Draw the pieces of your chest of drawers and measure the components.
![]() Save your responses in your course folder.
Save your responses in your course folder.
1.11. Lesson 2 Summary
Module 6: Measurement
Lesson 2 Summary

Stockbyte/Thinkstock
In this lesson you discovered that every measurement has a relative margin of error. This error is called uncertainty. Uncertainty is related to the precision of the measuring device and unless otherwise stated, the uncertainty is one-half of the precision.