Lesson 1
| Site: | MoodleHUB.ca 🍁 |
| Course: | Math 30-2 SS |
| Book: | Lesson 1 |
| Printed by: | Guest user |
| Date: | Wednesday, 24 December 2025, 6:21 AM |
Description
Created by IMSreader
1. Lesson 1
Module 1: Logic and Set Theory
Lesson 1: Strategy in Games, Puzzles, and Patterns
Focus

Goodshoot/Thinkstock
Have you ever noticed how two people can be playing the same game but have two completely different strategies? Understanding your opponent’s strategy is very important in games like chess or role-playing games. In these types of games, the success of your next move is dependent on your opponent’s move.
Understanding strategy can also help to improve your success with one-player games or puzzles. You probably already adapt your strategy based on what works and what doesn’t work. This is part of becoming a better player whether you are playing against yourself, a real opponent, or a virtual opponent.
Lesson Outcomes
At the end of this lesson, you will be able to
-
use numerical and logical reasoning to develop problem-solving strategies to analyze puzzles and games
-
observe and analyze other peoples’ personal strategies
-
develop your own personal problem-solving strategies to solve logic problems, puzzles, or games
Lesson Question
In this lesson you will investigate the following question: How can different personal strategies be used to solve a puzzle or win a game?
Assessment
Your assessment may be based on a combination of the following tasks:
-
completion of the Lesson 1 Assignment (Download the Lesson 1 Assignment and save it in your course folder now.)
-
course folder submissions from Try This and Share activities
-
work under Project Connection
Self-Check activities are for your own use. You can compare your answers to suggested answers to see if you are on track. If you have difficulty with concepts or calculations, contact your teacher.
Remember that the questions and activities you will encounter provide you with the practice and feedback you need to successfully complete this course. You should complete all questions and place your responses in your course folder. Your teacher may wish to view your work to check on your progress and to see if you need help.
Time
Each lesson in Mathematics 30-2 Learn EveryWare is designed to be completed in approximately two hours. You may find that you require more or less time to complete individual lessons. It is important that you progress at your own pace, based on your individual learning requirements.
This time estimation does not include time required to complete Going Beyond activities or the Module Project.
1.1. Discover
Module 1: Logic and Set Theory
Discover
Jeffrey Banke/iStockphoto/Thinkstock
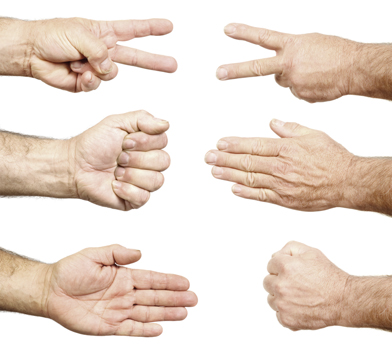
Take a minute and think back to the last time you played rock, paper, scissors against one of your friends. Did you win? lose? draw? What strategy did you use? There are many ways that you can win at rock, paper, and scissors, but is there a strategy that works all the time?
Strategies for solving a puzzle or winning a game can be quite different. One strategy is not necessarily better than another. Each strategy has its own strengths and weaknesses, and some are more appropriate in certain situations while others are not. In fact, participants may change their strategy several times throughout a game based on their own performance or an opponent’s performance.
Imagine a chess match where one opponent’s moves might change from defensive to offensive in order to win or a curling game where a rock is sacrificed to set a guard to save or gain a point. These are strategies designed to help someone win a game.
Try This 1

marinini/iStockphoto/Thinkstock
Logic puzzles can be very challenging. Reading each word carefully is the key to solving the puzzle. Use a variety of problem-solving techniques that you have learned from past courses to help you solve the Sport Kids Puzzle.
Sport Kids Puzzle
The young girls in this puzzle are Diane, Jackie, and Sarah. The young boys are Chuck and Harry.
From the clues provided, determine what
- sport each young person plays: baseball, basketball, soccer, swimming, volleyball
- town they are from: Calgary, Edmonton, Red Deer, Sherwood Park, St. Albert
- their father does for a living: baker, carpenter, mechanic, real-estate agent, teacher
Clue 1: The soccer player’s father is a real-estate agent. The mechanic is the father of neither Harry nor the baseball player.
Clue 2: The teacher’s daughter from Red Deer is neither Jackie nor the swimmer.
Clue 3: Diane is playing division 1 volleyball. Sarah’s father is not the mechanic.
Clue 4: The basketball player lives in St. Albert.
Clue 5: Chuck's father is a baker who neither lives nor works in Sherwood Park.
Clue 6: Sarah, who lives in Calgary, is not a baseball player.
Clue 7: Harry has no interest in swimming or basketball.
Clue 8: The retired carpenter and his daughter drove to Edmonton, where one of the other players lives, for a competition.
Clue 9: Chuck was scheduled to play an away game in Red Deer, but the game was rained out.
Clue 10: Sarah is the only athlete that does not compete as part of a team.
![]() Save your responses in your course folder.
Save your responses in your course folder.
Share 1
Compare your strategy for solving the Sport Kids Puzzle with another student or group. Discuss with your teacher how you will connect with other students for Share activities in this course. This may be done in person or virtually. For instance, you may want to post your response to the discussion board or have a video conference with another student. For more information on Share discussions, refer to the Course Introduction.
In your discussion, answer the following questions:
- What were the similarities and differences between the strategies used?
- Were all the strategies successful?
- Is there more than one possible solution? If so, what is it?
![]() If required, place a summary of your discussion in your course folder.
If required, place a summary of your discussion in your course folder.
In the Sport Kids Puzzle, a different strategy may have been used by you and your partner. The success of a strategy in this case is based on guessing what sport each child played, what town they are from, and what their father does for a living. To learn more, open the piece titled Sport Kids Puzzle Solution.
1.2. Explore
Module 1: Logic and Set Theory
Explore
A personal strategy is an individual approach to a situation or problem using words or mathematical processes.
Developing a personal strategy involves thinking about the situation or problem, planning how to solve the problem or situation, carrying out the plan, and, finally, evaluating the solution. The key is to be creative. Some strategies may include the following:
- using diagrams, lists, and/or charts
- looking for patterns
- guessing and checking
- eliminating possibilities
- working backwards
- simplifying or rewording the original problem
Did you use any of these strategies when you solved the Sport Kids Puzzle?
Try This 2
![]()
- Complete “The Strategy” questions B, C, D, E, and F on page 55 of your textbook.
Save your responses in your course folder. For question 1, you may want to create screen captures from Carol’s Puzzle Solution and place those in your course folder.
1.3. Explore 2
Module 1: Logic and Set Theory
In Try This 2 you had the opportunity to apply a personal strategy to solve a puzzle. Perhaps your strategy will work for other types of puzzles.
Now look at a variation of a logic puzzle called Einstein’s Problem. It is one of the most famous logic puzzles known and has many different variations. It is reported that only 2% of the population can figure it out on the first try!
Self-Check 1

© sarah5/27232067/Fotolia
Try your hand at this variation of the Einstein Problem.
There are five houses, each with a different colour. The home owners, each with a unique heritage, drink a certain type of beverage, eat a certain brand of dark chocolate, and keep a certain variety of pet. None of the owners have the same variety of pet, eat the same brand of chocolate, or drink the same beverage.
- house colours: blue, green, red, white, yellow
- nationalities: Brit, Dane, German, Norwegian, Swede
- brands of dark chocolate: Chocolovel, Dagoba Eclipse, Green and Black’s, Scharffen Berger, Valrhona
- beverages: coffee, juice, milk, tea, water
- pets: birds, cats, dogs, fish, horse
From the clues provided, who owns the pet fish?
Clue 1: The Brit lives in the red house.
Clue 2: The Swede keeps dogs as pets.
Clue 3: The Dane drinks tea.
Clue 4: Looking from in front, the green house is just to the left of the white house.
Clue 5: The owner of the green house drinks coffee.
Clue 6: The person who eats Valrhona dark chocolate raises birds.
Clue 7: The owner of the yellow house eats Chocolovel dark chocolate.
Clue 8: The man living in the centre house drinks milk.
Clue 9: The Norwegian lives in the leftmost house.
Clue 10: The man who eats Green and Black’s dark chocolate lives next to the one who keeps cats.
Clue 11: The man who keeps a horse lives next to the man who eats Chocolovel dark chocolate.
Clue 12: The owner who eats Dagoba Eclipse dark chocolate also drinks juice.
Clue 13: The German eats Scharffen Berger dark chocolate.
Clue 14: The Norwegian lives next to the blue house.
Clue 15: The man who eats Green and Black’s dark chocolate has a neighbour who drinks water.
Not sure how that solution is found? Watch an animation of the Solution to Einstein’s Problem.
image: © sarah5/27232067/Fotolia
1.4. Explore 3
Module 1: Logic and Set Theory
In the next Try This activity you will use numerical reasoning to solve puzzles. If you don’t solve the puzzle one way, try another strategy!
Try This 3
- Place the numbers 2, 2, 2, 3, 3, 3, 4, 4, and 4 in a three-by-three grid like the following so that when any line of three numbers is added up in any direction, including diagonally, the sum is always 9. Explain the strategy that you used to solve this puzzle.
-
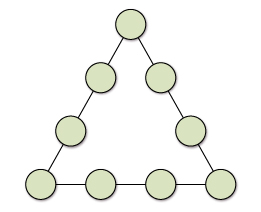
Kenton tried to solve the following puzzle:
Use the numbers 1 to 9 in each circle of the triangle so that the four numbers along each edge add up to the same total.
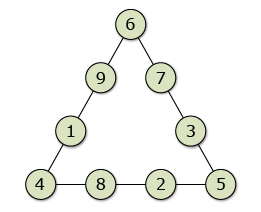
Kenton's solution to the puzzle is shown. Explain if Kenton’s solution is correct.
![]() Save your responses in your course folder.
Save your responses in your course folder.
1.5. Connect
Module 1: Logic and Set Theory
Connect
Lesson 1 Assignment
Complete the Lesson 1 Assignment that you saved in your course folder at the beginning of this lesson. When you do the assignment questions, explain the strategies you used to solve the puzzles.
Your Lesson Assignment contains some problems for you to solve using the new knowledge gained during the lesson. You will also have the chance to apply the concepts and strategies that you have learned to a new situation. Show work to support your answers.
Project Connection
You are ready to start working on Module 1 Project: Logic Puzzles. Go to the Module 1 Project and read over all project requirements to become familiar with what you will be doing and how you will be assessed. Now complete Part 1 of the project.
1.6. Lesson 1 Summary
Module 1: Logic and Set Theory
Lesson 1 Summary

Hemera Technologies/
AbleStock.com/Thinkstock
Different strategies can be used to solve puzzles and win games. Knowing your personal strategy and being able to adapt your strategy as required can help you improve your success with games or puzzles. Sharing your approach is another way to gain useful information. An opponent or fellow teammate may have a different way of approaching the game or puzzle. You may choose to incorporate all, a part, or none of the other person’s strategy into your game play. You will explore game strategies in upcoming lessons.
In the next lesson you will investigate how using set theory can be used to help develop winning strategies.


