Lesson 3
| Site: | MoodleHUB.ca 🍁 |
| Course: | Math 30-2 SS |
| Book: | Lesson 3 |
| Printed by: | Guest user |
| Date: | Wednesday, 24 December 2025, 4:27 AM |
Description
Created by IMSreader
1. Lesson 3
Module 1: Logic and Set Theory
Lesson 3: Applications of Sets
Focus

IT Stock Free/Polka Dot/Thinkstock
In small schools, many students play on multiple sports teams. Scheduling games can be challenging since many players are on multiple teams.
Consider the following example.
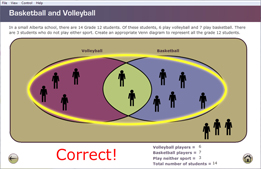
In a small Alberta school, there are 14 Grade 12 students. Of these students, 6 play volleyball and 7 play basketball. There are 3 students who do not play either sport.1 The total number of students adds up to 16, but how is this possible if there is a total of only 14 Grade 12 students?
Set notation can help solve problems similar to this one by determining how many players play each sport, how many players play both sports, and how many students don’t play either sport. From that information, schedules can be made that don’t overlap and thus avoid forcing any student on more than one sports team to miss any games.
How would you solve this problem?
Lesson Outcomes
At the end of this lesson, you will be able to
- describe how to use the principle of inclusion and exclusion when solving problems involving the union of sets
- solve problems involving unions and intersections of sets
Lesson Questions
In this lesson you will investigate the following questions:
- What do the words and, or, and not represent in set theory questions?
- How can set theory be used to solve problems?
Assessment
Your assessment may be based on a combination of the following tasks:
- completion of the Lesson 3 Assignment (Download the Lesson 3 Assignment and save it in your course folder now.)
- course folder submissions from Try This and Share activities
- additions to Glossary Terms and Formula Sheet
- work under Project Connection
1 Adapted from PRINCIPLES OF MATHEMATICS 12 by Canavan-McGrath et al. Copyright Nelson Education Ltd. Reprinted with permission.
1.1. Discover
Module 1: Logic and Set Theory
Discover
You were introduced to this problem in the Focus section: In a small Alberta school, there are 14 Grade 12 students. Of these students, 6 play volleyball and 7 play basketball. There are 3 students who do not play either sport.
Try This 1
Now use the applet titled Basketball and Volleyball to create an appropriate Venn diagram for the problem described in Focus.
![]()
Share 1
With a partner or in a group, come to agreement on the following questions regarding Try This 1.
- Explain why the following statement is false:
volleyball players + basketball players + play neither sport = total number of students - Write a mathematical statement similar to the sum in question 1 that is correct.
1.2. Explore
Module 1: Logic and Set Theory
Explore
The sports example from the Focus section is an example that involves the intersection of sets and the union of sets. Examples in previous lessons also included intersections and unions; however, in this lesson you will examine intersections and unions in more detail.
The set of elements that are common to two or more sets is called the intersection of those sets. Mathematicians use the symbols A ∩ B to signify the intersection of sets A and B.1 Sets that have no elements in their intersection are said to be disjoint.
All elements that are counted are considered to be in the universal set. This is usually represented by drawing a box around the Venn diagrams. The universal set can be thought of as the set that contains all other sets. For example, if the set C = {consonants}, the universal set is the alphabet.
You may also find a set that has no elements in it. This is known as the empty set or null set. For example, for the set X = {days of the week starting with the letter “J”} is an empty set. An empty set is written as { }, so, for the example, this would be written as X = { }.
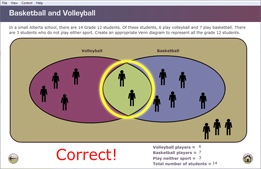
In the sports example from Focus, there are two students in the intersection of the volleyball and basketball sets, as shown by this Venn diagram.
The set of all elements in two or more sets is called the union of those sets. Mathematicians use the symbols A ∪ B to signify the union of sets A and B.2
In the sports example from Focus, there are eleven students in the union of the volleyball and basketball sets, as shown by the following Venn diagram.
The following examples may help you understand these terms better.
| Sets | Intersection | Union |
F = {red, blue, green} H = {red, purple} |
F ∩ H = {red} |
F ∪ H = {red, blue, green, purple} |
A = {1, 2, 3, 4} B = {3, 4, 5} |
A ∩ B = {3, 4} |
A ∪ B = {1, 2, 3, 4, 5} |
J = {1, 3, 5, 7} B = {2, 4, 6, 8} |
J ∩ B = { } There are no elements in this set. (It is the empty set.) Therefore, sets J and B are disjoint. |
J ∪ B = {1, 2, 3, 4, 5, 6, 7, 8} |
You may also want to read “Communication: Notation” on page 23 of your textbook for descriptions of union and intersection using Venn diagrams. Note how the textbook explains that the notation A \ B is read as “A minus B” to signify the set of elements that are in set A but not in set B.
Self-Check 1
- Complete “Check Your Understanding” questions 1 and 2 on page 32 of your textbook. Note: For question 2, you may want to complete part b. first and then use the Venn diagram to answer part a. Answers
- Complete “Practising” question 6 on page 33 of your textbook. Answers
1, 2Adapted from PRINCIPLES OF MATHEMATICS 12 by Canavan-McGrath et al. Copyright Nelson Education Ltd. Reprinted with permission.
1.3. Explore 2
Module 1: Logic and Set Theory
Now some terminology is required to describe the sports problem from Focus. You may have discovered that the total number of students playing volleyball or basketball is not simply the sum of students playing volleyball and students playing basketball. This can be written using set notation as
n(volleyball ∪ basketball) ≠ n(volleyball) + n(basketball)
The reason for this is that students who play both volleyball and basketball will be counted twice—once when counting the volleyball players and once when counting the basketball players. To get a correct total, you must subtract the number of students that play both sports—the intersection of those two sets. Using set notation, this becomes the following:
n(volleyball ∪ basketball) = n(volleyball) + n(basketball) − n(volleyball ∩ basketball)
Mathematicians call this the principle of inclusion and exclusion. For any sets A and B, the following is always true:
n(A ∪ B) = n(A) + n(B) − n(A ∩ B)
To learn more, view the multimedia piece titled Principle of Inclusion and Exclusion.
![]()
For further information about the principle of inclusion and exclusion, you may wish to read “Need to Know” on page 31 of your textbook.
Self-Check 2
- A group of 28 adults were surveyed about their game-playing habits. The results are shown in the Venn diagram.
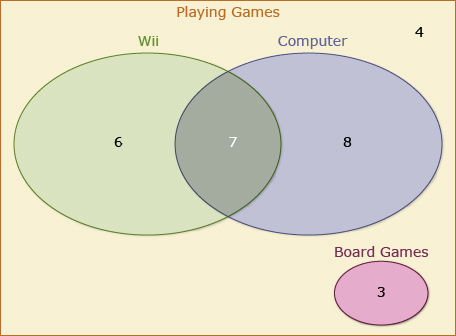
Using the following set notation, answer the questions.
P = {all adults surveyed}
W = {adults who play the Wii}
C = {adults who play on the computer}
B = {adults who play board games}- n{W ∪ C}
- n{W \ C}
- n{W ∩ C}
- n{W ∩ B} (What are sets W and B called in relation to each other?)
-
Describe the elements in the complement of {W ∪ C}.
![]()
- Complete “Practising” questions 8 and 9 on page 33 of your textbook. Answers
So far, this lesson has described unions and intersections as they relate to set theory application. In the next Try This activity, you will see the use of new terms that are connected to union and intersection. The new terms are and, or, and not.
Try This 2
When studying the relationship between the union and intersection of sets, there is some new terminology you need to be comfortable using correctly.
The short multimedia piece titled And, Or, and Not will introduce you to the use of the words and, or, and not in the context of union and intersection of sets seen earlier in the Basketball and Volleyball example.
1.4. Explore 3
Module 1: Logic and Set Theory
You may have discovered in Try This 2 that the words and, or, and not can be used to describe different areas of a Venn diagram. The intersection of sets A and B can also be described as the set of elements in “A or B.” The union of sets A and B can also be described as the set of elements in “A or B.” The complement of A and B is described as the set of elements “not in A and B.”
Read “Mid-Chapter Review” on pages 36 and 37 of your textbook. Note the use of the words and, or, and not as well as the use of the other set theory terminology.
In the next activity you will see how set theory can be useful for analyzing real-world problems.
Try This 3
Complete “Investigate the Math” questions A, B, C, D, and E on page 22 of your textbook. Creating a Venn diagram in the order described will make it easier to solve this problem. You may also find it useful to work with a partner on this problem.
![]() Save your responses in your course folder.
Save your responses in your course folder.
Share 2
Share your final Venn diagram with a partner. If your diagram differs from the one created by your partner, try to come to agreement on a correct Venn diagram.
![]() If required, save a record of your discussion in your course folder.
If required, save a record of your discussion in your course folder.
The principle of inclusion and exclusion can be extended to solve examples that involve three sets that intersect.
Consider the next scenario. Each member of a sports club plays at least one of the following sports: soccer, rugby, or tennis.

"Nuno Garuti"/Hemera/Thinkstock
The following information is given:
- 163 play tennis.
- 36 play tennis and rugby.
- 13 play tennis and soccer.
- 6 play all three sports.
- 11 play soccer and rugby.
- 208 play rugby or tennis.
- 98 play soccer or rugby.
Use this information to
- draw a Venn diagram
- determine the number of members in the club
A possible solution would be as follows.
- Draw a Venn diagram to represent the club and the three sports.
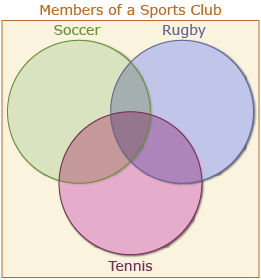
From the information provided, 6 people play all three sports; therefore, you can fill in the middle intersecting part with a 6.
n(S ∩ R ∩ T) = 6
You can also fill in the intersecting regions for two sports.
- 36 play tennis and rugby. (Subtract the 6 from the middle region and n(T ∩ R) = 30.)
- 13 play tennis and soccer. (Subtract the 6 from the middle region n(T ∩ S) = 7.)
- 11 play soccer and rugby. (Subtract the 6 from the middle region n(S ∩ R) = 5.)
Put these numbers into the Venn diagram.
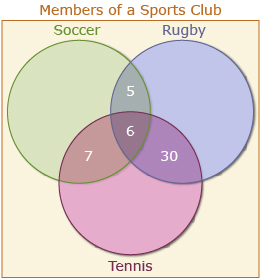
Using the information that 163 play tennis, subtract the other regions in the tennis circle. The outer region is 163 − 6 − 7 − 30 = 120.
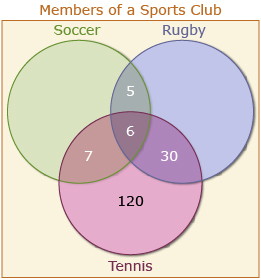
Now use the last two pieces of information that tell you about the union of sets to find the remaining regions: 208 play rugby or tennis.
This is the region (R ∪ T). Since all the other regions in these two circles is known, subtract the numbers from 208 to find the outer region in the rugby circle.
208 − 120 − 30 − 5 − 6 − 7 = 40
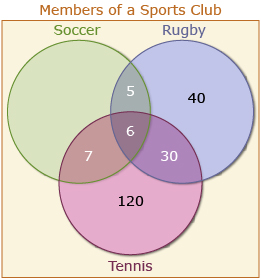
And finally, 98 people play soccer or rugby.
To find the outer region in soccer, you get 98 − 40 − 30 − 5 − 6 − 7 = 10.
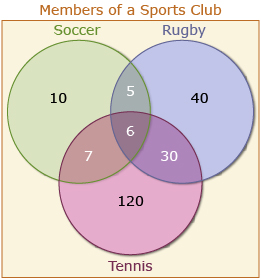
b. Add all the regions up and you find that this sports club has 10 + 5 + 6 + 7 + 40 + 30 + 120 = 218 members.
1.5. Explore 4
Module 1: Logic and Set Theory
Read “Example 1” on page 40 of your textbook. Study the solution on page 41. This example is different than the preceding example about the sports club members. In the textbook example, you are given the total number of children with a pet and you are asked to find different pieces of information. The formula calculation will be slightly different. Note: You would be provided with this formula if you were asked to solve a similar type of problem.
The multimedia piece titled Hailey’s Solution demonstrates how Hailey got to the starting point of her solution to the puzzle.
Self-Check 3
Complete the following questions from your textbook.
- “Practising” questions 5, 6, and 10 on pages 51 to 53
Note: For question 6, using S for swimming, C for cycling, and R for running would be
n(S) + n(C) + n(R) − n(S ∩ C) − n(C ∩ R) − n(S ∩ R) + n(S ∩ C ∩ R) = n(S ∪ C ∪ R)
Answers - “Practising” question 11 on page 33
Answers
Add the following terms to your copy of Glossary Terms:
- intersection
- union
- disjoint
- principle of inclusion and exclusion
- and, or, and not
- empty set
For each new definition in your glossary, be sure to include the appropriate notation.
Add the formula for the principle of inclusion and exclusion to determine the number of elements in the union of three sets.
n(A) + n(B) + n(C) − n(A ∩ C) − n(A ∩ B) − n(B ∩ C) + n(A ∩ B ∩ C) = n(A ∪ B ∪ C)
1.6. Connect
Module 1: Logic and Set Theory
Connect
Lesson 3 Assignment
Complete the Lesson 3 Assignment you saved in your course folder at the beginning of this lesson.
Project Connection
Go to the Module 1 Project and complete Part 3, which includes the conclusion. You should submit your completed Module 1 Project to your teacher for assessment after you have completed Part 3.
1.7. Lesson 3 Summary
Module 1: Logic and Set Theory
Lesson 3 Summary
In this lesson you learned about unions and intersections of sets. You represented unions and intersections by using Venn diagrams and the connecting words and, or, and not, as well as proper mathematical notation.
The diagrams on page 31 of your textbook provide a good summary of these terms.
You also used these concepts to solve real-world problems using sets and the principle of inclusion and exclusion. Using the skills you built in this lesson, you have seen that many items with similarities and differences can be described mathematically. The use of sets will show others your thought process behind the inclusion of items within a set and your ability to describe scenarios mathematically.
In Module 2 you will learn about odds and probabilities where the application of set theory can be very helpful and useful. But first, go to Lesson 4, which provides an overview of the course project you will encounter in Mathematics 30-2.