Lesson 1
| Site: | MoodleHUB.ca 🍁 |
| Course: | Math 30-2 SS |
| Book: | Lesson 1 |
| Printed by: | Guest user |
| Date: | Wednesday, 24 December 2025, 2:49 PM |
Description
Created by IMSreader
1. Lesson 1
Module 2: Probability
Lesson 1: Odds and Probability
Focus

Thinkstock Images/Comstock//Thinkstock
What are the odds of winning something—anything? Some people feel they never get lucky while others seem to get on lucky streaks and win everything! Go to the Internet and try to find odds for the following: odds for bowling a 300 game; odds of getting a hole in one in golf; odds for winning an Olympic medal; odds of “winning solitaire” on the computer. How might an understanding of odds help you make decisions?
How are these odds calculated? How do you know if they are valid?
In this lesson you will learn the answers to these questions and be able to use that knowledge to help make decisions and solve contextual problems involving probability and odds.
Lesson Outcomes
At the end of this lesson, you will be able to
- calculate the odds of events
- find probability from the odds and vice versa
- solve contextual problems involving odds and probability
- assess and make decisions based on odds and probability statements
Lesson Questions
You will investigate the following questions:
- What is the relationship between probability and odds, and how are they calculated?
- How does an understanding of probability and odds help you make decisions and solve contextual problems?
Assessment
Your assessment may be based on a combination of the following tasks:
- completion of the Lesson 1 Assignment (Download the Lesson 1 Assignment and save it in your course folder now.)
- course folder submissions from Try This and Share activities
- additions to Glossary Terms and Formula Sheet
- work under Project Connection
Self-Check activities are for your own use. You can compare your answers to suggested answers to see if you are on track. If you are having difficulty with concepts or calculations, contact your teacher.
Remember that the questions and activities you will encounter provide you with the practice and feedback you need to successfully complete this course. You should complete all questions and place your responses in your course folder. Your teacher may wish to view your work to check on your progress and to see if you need help.
Time
Each lesson in Mathematics 30-2 EveryWare is designed to be completed in approximately two hours. You may find that you require more or less time to complete individual lessons. It is important that you progress at your own pace, based on your individual learning requirements.
This time estimation does not include time required to complete Going Beyond activities or the Module Project.
1.1. Launch
Module 2: Probability
Launch
Do you have the background knowledge and skills you need to complete this lesson successfully? Launch will help you find out.
Before beginning this lesson, you should be able to
- differentiate between theoretical and experimental probability
- change between fractions, ratios, and percentages
- calculate probability
1.2. Are You Ready?
Module 2: Probability
Are You Ready?
Complete these questions. If you experience difficulty and need help, visit Refresher or contact your teacher.
- What is the difference between theoretical and experimental probability? Answer
- Convert between fractions, ratios, and percentages by completing the following table.
Fraction
Ratio
Percentage

3 : 5
45%
Answer - When a fair six-sided die is rolled, what is the probability that it will land on the five? Answer
If you answered the Are You Ready? questions without difficulty, move to Discover.
If you found the Are You Ready? questions difficult, complete Refresher.
1.3. Refresher
Module 2: Probability
Refresher
Go to Theoretical Probability and Experimental Probability from Mathematics Glossary.
Review how to convert ratios to fractions by viewing “Ratios as Fractions in Simplest Form.”
Review how to convert percent to fractions using the video “Representing a Number as a Decimal, Percent, and Fraction.”
Review probability using the video “Basic Probability: An Introduction to Probability.”
Go back to the Are You Ready? section and try the questions again. If you are still having difficulty, contact your teacher.
1.4. Discover
Module 2: Probability
Discover
Read “Explore the Math” on page 140 of your textbook. You will use the information in the textbook to answer question 1 of Try This 1.
Try This 1
- Use tables similar to the following to help list all the possible outcomes for one turn of Sasha's game and who wins each turn.
Note that for the tables, it does not matter which player has the horizontal numbers and which player has the vertical numbers since the winner is determined by the sum or product of the numbers—not who drew the numbers.
Product
1
2
3
1
1
2
4
3
6
Sum
1
2
3
1
2
2
4
3
5
Winner
1
2
3
1
player 1
2
tie
3
player 2
![]()
-
- Complete “Reflecting” questions A, B, and C on page 140 of your textbook.
- Is Sasha’s game a fair game? Explain.
![]() Save your responses in your course folder.
Save your responses in your course folder.
Share 1
Try playing Sasha’s game with a partner. Keep track of how many times each player wins. How does this compare with your answer to “Reflecting” question C?
![]() If required, save your discussion in your course folder.
If required, save your discussion in your course folder.
1.5. Explore
Module 2: Probability
Explore
In golf, getting a hole in one is every golfer's dream. In Focus did you go to the Internet and find odds of getting a hole in one? Odds are another way to discuss the probability of an event. In Discover you calculated the theoretical probability and the experimental probability of winning a game. These probabilities can also be described using odds. In the next Try This activity, you will examine the relationship between probability and odds.
Try This 2

Hemera/Thinkstock
Suppose you are watching a game show on TV. Five green doors are shown. Contestants on the show get to choose a door and potentially win a prize. Prizes can be found behind two of the five doors.
- Determine the probability of winning a prize.
- Determine the probability of not winning a prize.
- Add the probability of winning and not winning a prize. What do you notice?
- The answers for questions 1 and 2 could be used to calculate the odds of winning and the odds of not winning. Use the following formula to write the odds as a fraction.
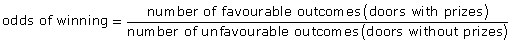
- Write the odds of winning as a ratio.
odds in favour of A = number of outcomes for A : number of outcomes against A
-
Write the odds against winning as a ratio.
![]() Save your responses in your course folder.
Save your responses in your course folder.
Share 2
With a partner or in a group, discuss the following questions based on your responses to Try This 2.
-
- How does the probability of winning a prize compare to the odds of winning a prize?
- What similarities and differences do you notice between expressing the probability and the odds for an event?
- What do you notice about the odds for winning versus the odds against winning? What relationship do you see?
1.6. Explore 2
Module 2: Probability
In Share 2, a few different relationships were observed.
You saw that the probability of winning added to the probability of not winning equals 1. The formula used to describe the probability of an event and its complement is ![]() .
.
In the case of the door prizes, it would look like this:

In Try This 2 you used the odds formula to find the odds of winning and the odds against winning as fractions and ratios:
![]()
Or
odds in favour of A = number of outcomes for A : number of outcomes against A
You may have also noticed the relationship between the odds of winning and the odds against winning:
- odds for winning → 2 : 3
- odds against winning → 3 : 2
Notice how the ratio for the odds is reversed.
You may also have noticed the connection between probability and odds. Probability is based on winning a prize out of all of the possibilities, whereas odds are based on winning a prize compared to not winning a prize.
The difference between odds and probability is this:
- Probability is based on favourable outcomes in relation to the total number of possible outcomes.
- Odds are based on the favourable outcomes “for” in relation to unfavourable outcomes “against.”
1.7. Explore 3
Module 2: Probability
Read “Example 1” on page 143 to see another example of how to calculate the odds. As you read, note how set notation is used to indicate the cards you are interested in choosing. The set notation used in the example is related to the odds formula:
![]()
Self-Check 1
![]()
- Complete “Your Turn” on page 143 of your textbook. Answer
- What is the probability of not drawing a heart in a random draw from a standard deck of 52 playing cards? Answer
- The probability that it will rain in Edmonton today is 0.53. What is the probability that it will not rain in Edmonton today? Answer
- Answer question 3 on page 148 of your textbook. Answer
In Try This 2 you were given information, and, from that, you calculated the probability and the odds. What if the information was not given, only the probability? How can you get the information you need in order to determine the odds? The following activity shows how odds can be determined from a probability statement.
Try This 3
There is a 10% probability of winning a free play in the charity draw.
- Write 10% as a fraction.
- If 100 tickets are purchased, theoretically how many tickets would win a free play?
- If 100 tickets are purchased, theoretically how many tickets would not win a free play?
- Based on a 100 tickets being sold, what are the odds in favour of winning a free play? Write your answer as a ratio; then write it as a reduced ratio.
- Describe in words the information you can gain from knowing the probability of an event and how this information helps you write the odds for the event.
![]() Save your responses in your course folder.
Save your responses in your course folder.
1.8. Explore 4
Module 2: Probability
Go to page 144 of the textbook and read “Example 2.” As you read, pay special attention to how odds are determined given just the probability.
Self-Check 2
Complete “Your Turn” on page 144 of your textbook. Answer
You have been determining the odds from a probability statement, but you can also determine the probability when given the odds. Read “Example 3” on pages 144 and 145 of your textbook. Note how the total number of outcomes is found from the odds ratio.
Self-Check 3
1.9. Explore 5
Module 2: Probability
Many probabilities and odds are based on actual data and not just “some” number pulled out of thin air. Weather forecasts and cancer survival rates are some examples where the probabilities and the odds are calculated based on real information. These odds and probabilities are assessed and then used to make decisions for upcoming events.
Compare these same statistics that have been presented or framed differently. How does the framing affect your decision?
Column charts are again very popular, but as you see below, the perception of the importance of a change in risk can be manipulated by altering the scale of the column—the effect of eating bacon looks a lot larger in the second chart, yet it is the same 1% increase.
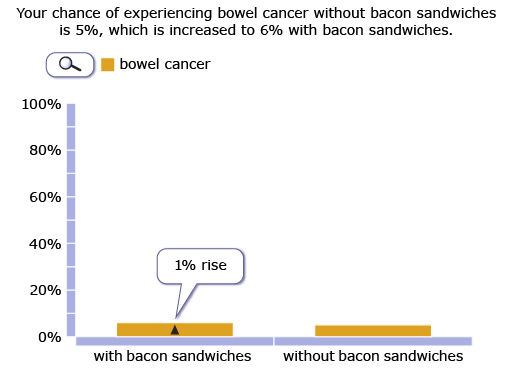
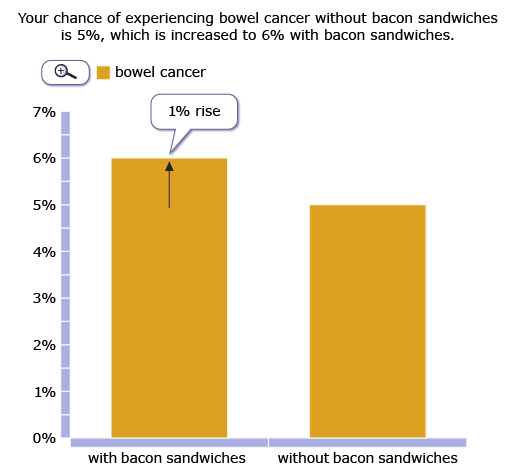
This material first appeared on the Understanding Uncertainty website http://understandinguncertainty.org.
Try This 4
- Find examples of statements of probability and odds found in the media, biology, sports, medicine, sociology, or psychology.
- Using an example from question 1, how would knowing this probability or these odds affect a decision you would make?
![]() Save your responses in your course folder.
Save your responses in your course folder.
Share 3
With a partner or in a group, share your examples from Try This 4 and provide an explanation of how knowing the probability and odds might affect a decision you would make.
1.10. Explore 6
Module 2: Probability
Probability and odds can be used to make decisions that may have a significant impact on an event. For example, imagine that game 7 of the Stanley Cup final will be decided by a shootout after a five-minute overtime period. Imagine the pressure on the coach to make the right decision about which players to choose for the shootout.

Ron Chapple Studios/Thinkstock
Read “Example 4” on pages 145 and 146 of your textbook. This is a good example of making a decision based on odds and probability to try to win a hockey game—but not game 7 of the Stanley Cup! The information that the coach has to work with is based on real data and, therefore, the calculation of the odds and probability would be valid.
Self-Check 4
1.11. Explore 7
Module 2: Probability
In Try This 4 you found odds and probability statements in the media. You thought about how these statements might influence your decisions. Read “Example 5” that shows how odds can be used to make a decision about which game to play on page 146 of your textbook. Pay attention to both Madison’s solution, which uses probability, and Samara’s solution, which uses odds.
Self-Check 5
- Complete “Your Turn” on page 147 of your textbook. Answer
- Complete question 17 on page 150 of your textbook. Answer

Photos.com/Thinkstock
Blaise Pascal was not only a brilliant mathematician, but he was also a physicist and an inventor. He laid the groundwork for the study of probability. He also invented a calculating device that could do the basic arithmetic operations of addition, subtraction, multiplication, and division.
It is said that a gambling dispute between two players in the 1600s led Pascal to investigate probability theory. The original game consisted of throwing a pair of dice 24 times and betting money on the outcome of double sixes. Pascal was asked to calculate the chances that this would happen. He showed the gamblers that double sixes was not as likely an outcome as they had originally thought. How could he have done this?
Type “Pascal’s calculator” into your favourite search engine to see a picture of the machine and a description of how it was used.
In addition to his accomplishments, Pascal is said to have been the first person to wear a wrist watch!
Add odds to your copy of Glossary Terms.
Add the following formulas to your copy of Formula Sheet.
![]()
Or
odds in favour of A = number of outcomes for A : number of outcomes against A
![]()
1.12. Connect
Module 2: Probability
Complete the Lesson 1 Assignment that you saved in your course folder at the beginning of the lesson. Show work to support your answers.
![]() Save your responses in your course folder.
Save your responses in your course folder.
Project Connection
You are ready to start working on Module 2 Project. Go to the Module 2 Project: Carnival Probabilities, and read Project Overview to become familiar with what you will be doing and how you will be assessed. At this time, only read through the project. You will begin the project in Lesson 2.
Going Beyond
Sometime on September 24, 2011, NASA’s Upper Atmosphere Research Satellite (UARS) fell to Earth and plunged into the Pacific Ocean. There is always concern about someone being hit when an object falls “from the sky.” The chances, however, of being hit are extremely small and there are calculations done to prove it.

Hemera/Thinkstock
According to NASA’s calculations, the odds in favour of a person being hit are 1 : 3200, and the odds of you being hit are even more remote at 1 : 22 400 000 000 000.
But how are these odds calculated—and are they believable? Try to find information about how these odds were calculated.