Lesson 2
| Site: | MoodleHUB.ca 🍁 |
| Course: | Math 30-2 SS |
| Book: | Lesson 2 |
| Printed by: | Guest user |
| Date: | Wednesday, 24 December 2025, 12:42 PM |
Description
Created by IMSreader
1. Lesson 2
Module 2: Probability
Lesson 2: Mutually Exclusive and Non-Mutually Exclusive Events
Focus
Have you ever won, or know of anyone who’s won, money playing the lottery? Have you ever been, or know of someone who has been, struck by lightning? Which of these two events do you think is more likely to happen? Do you think both events could happen to someone at the same time, or do you think that only one of the events could happen to someone?
Type “lottery winner struck by lightning” into your favourite search engine, and see if you can find anyone who has
- won the lottery and been hit by lightning
- won the lottery only
- been hit by lightning only

soccer player: © olly/12890052/Fotolia, lottery ticket: iStockphoto/Thinkstock
Lesson Outcomes
At the end of this lesson, you will be able to
- classify, determine, and represent, using set notation and graphic organizers, mutually exclusive and non-mutually exclusive events
- solve contextual problems that involve the probability of mutually exclusive events and non-mutually exclusive events
- create and solve contextual problems that involve the probability of mutually exclusive events and non-mutually exclusive events
Lesson Question
In this lesson you will answer the following question: How are problems that involve mutually exclusive and non-mutually exclusive events solved?
Assessment
Your assessment may be based on a combination of the following tasks:
- completion of the Lesson 2 Assignment (Download the Lesson 2 Assignment and save it in your course folder now.)
- course folder submissions from Try This and Share activities
- additions to Glossary Terms and Formula Sheet
- work under Project Connection
1.1. Launch
Module 2: Probability
Launch
Do you have the background knowledge and skills you need to complete this lesson successfully? Launch will help you find out.
Before beginning this lesson, you should be able to
- determine the probability of an event and its complement
- use set notation symbols: ∪ and ∩
1.2. Are You Ready?
Module 2: Probability
Are You Ready?
Complete these questions. If you experience difficulty and need help, visit Refresher or contact your teacher.
- Suppose E = {2, 4, 6, 8, 12} and O = {3, 6, 9, 12, 15}. Determine the following.
- The
 What would the complement be? Answer
What would the complement be? Answer
If you answered the Are You Ready? questions without difficulty, move to Discover.
If you found the Are You Ready? questions difficult complete Refresher.
1.3. Refresher
Module 2: Probability
Refresher
To refresh and review your understanding of set notation, read Math 30-2: Module 1: Lesson 2.
To refresh and review your understanding of complement, read Explore 2 of Math 30-2: Module 2: Lesson 1.
Go back to the Are You Ready? section and try the questions again. If you are still having difficulty, contact your teacher.
1.4. Discover
Module 2: Probability
Discover
Try This 1
Complete the following Try This questions as you work through the Sample Space for Rolling Two Dice multimedia piece. Keep the multimedia piece open. You will need it to answer the questions from Game A and Game B.
Janek and Violeta are playing a board game using two different sets of rules. Compare the probability between the two sets of rules to determine whether Janek will move on his turn.
Game A
In order to move, Janek must roll either doubles or a sum of 7 with two dice.
- Determine the probability of throwing doubles, P(throwing doubles).
- Determine the probability of rolling a of 7, P(sum of 7).
- Using a Venn diagram, can you calculate P(throwing doubles or rolling a sum of 7)? This is the probability Janek will move on his turn.
Game B
Janek and Violeta decide to change the rules. In order to move now, a player must either have a sum greater than or equal to 10 or a sum that is an even number with two dice.
Continue on to Game B of Sample Space for Rolling Two Dice. Try to solve the probability that Janek will move on his turn.
- Determine P(sum greater than or equal to 10).
- Determine P(even sum).
- Using a Venn diagram, can you calculate P(sum greater than or equal to 10 or an even sum)? This is the probability Janek will move on his turn.
![]() Save your responses in your course folder.
Save your responses in your course folder.
Share 1
Discuss the following questions with a partner or in a group.
- Compare the Venn diagrams from Game A and Game B. What is similar? What is different?
- When you calculated the probability in Game A, describe the procedure you used.
- When you calculated the probability in Game B, describe the procedure you used.
- Write a formula for calculating the probability P(throwing doubles or rolling a sum of 7)?
- Write a formula for calculating the probability P(sum greater than or equal to 10 or an even sum)?
1.5. Explore
Module 2: Probability
Explore

Zoonar/Thinkstock
In Discover, you used Sample Space of Rolling Two Dice and Venn diagrams to show the difference between events that have no common outcomes (set of rules for Game A) and events that have common outcomes (set of rules for Game B).
The set of rules for Game A only allowed Janek to move if either doubles were rolled or a sum of 7 was rolled. It would be impossible to roll doubles and a sum of 7 at the same time. When two events cannot occur at the same time, the events are said to be mutually exclusive.
The number of outcomes in the union of the two events is the sum of the outcomes in each event. This information can be summarized in the following diagram.
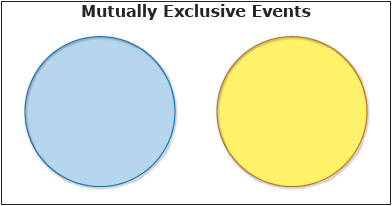
Mutually exclusive events do not share any common outcomes.
The set of rules for Game B only allowed Janek to move if he did one or the other of the following:
- rolled a sum greater than or equal to 10
- rolled a sum that is an even number
As you saw, both of these events can occur at the same time. For example, it is possible to roll a 6 and 6. The sum of 12 is both greater than 10 and is an even number. These events are considered non-mutually exclusive.

Non-mutually exclusive events share common outcomes. In the Venn diagram, the green area represents the common outcomes.
This diagram is used when one sees the word or and events from A and B can happen at the same time.
Try This 2
Create an example that is not used in this lesson to describe the difference between mutually exclusive and non-mutually exclusive events.
- Draw a Venn diagram that describes your example. Label the first event as Event A and the second as Event B.
- Indicate whether the example is mutually exclusive or non-mutually exclusive.
![]() Save your responses in your course folder.
Save your responses in your course folder.
Share 2
Share your example from Try This 2 with a partner or group. As you look at examples from other students, discuss the following.
- What similarities do you notice between Venn diagrams of the mutually exclusive examples?
- What similarities do you notice between Venn diagrams of the non-mutually exclusive examples?
1.6. Explore 2
Module 2: Probability
Self-Check 1
- Consider the following experiment:
A single card is chosen at random from a standard deck of 52 playing cards.
Determine whether the events are mutually exclusive or non-mutually exclusive. Use a Venn diagram to support your answer. -
Mutually exclusive and non-mutually exclusive events can also be applied to real-life scenarios.

iStockphoto/Thinkstock
In the National Hockey League, there are a number of ways for teams to earn points during the regular season. A regulation game is 60 minutes. A team that wins in regulation time gets 2 points; a team gets 0 points if it loses in regulation time.
If a game ends in a tie after regulation time, then there is a five-minute overtime period. If the game is still tied after overtime, a shootout follows. In a shootout, individual players take turns trying to score to win the game. This shootout continues until one team wins. In overtime or a shootout, the winning team gets 2 points and the losing team gets 1 point.
Using this information, answer the following questions:
![]()
- Complete questions 1.a. and 1.b. on page 176 of your textbook. Answer
1.7. Explore 3
Module 2: Probability
In Discover, you compared the probability that Janek would move on his next turn using two sets of rules. You now know that the rules in Game A were mutually exclusive and the rules in Game B were non-mutually exclusive. Did you notice that the probability calculation was different?
Read “Example 1” on page 167 of your textbook to see how the mutually exclusive formula is developed. The formula is summarized as follows:
P(A or B) = P(A) + P(B)
P(A ∪ B) = P(A) + P(B)
How might this formula be different for non-mutually exclusive events? Read “Example 2” on pages 168 and 169 of your textbook to see a probability calculation of events that are non-mutually exclusive. Remember that the elements in the union must be subtracted from the sum of the elements in each set when developing the probability formula for non-mutually exclusive events. The formula is summarized as follows:
P(A or B) = P(A) + P(B) − P(A and B)
P(A ∪ B) = P(A) + P(B) − P(A ∩ B)
Note: The non-mutually exclusive formula can also be used for mutually exclusive events because P(A and B) will be zero.
Self-Check 2
- A card is randomly selected from a standard deck of playing cards. To the nearest hundredth, determine the probability of a
- Graphic organizers are a good way to represent mutually exclusive and non-mutually exclusive events. Use the Venn diagram to answer the questions that follow.
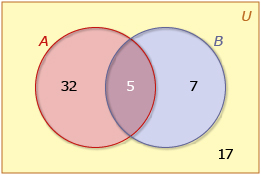
![]()
- Complete question 5 on page 177 of your textbook. Answer
- Complete questions 1.c. and 1.d. on page 176 of your textbook. Answer
- The integers from 1 to 12 inclusive are written on 12 separate slips of paper and placed in a hat. One slip is drawn at random from the hat. Rounded to the nearest hundredth, find the probability that the number is a
1.8. Explore 4
Module 2: Probability
So far, you’ve identified events as mutually exclusive, non-mutually exclusive, and complementary. In Lesson 1 you learned about probability and odds. Now you will learn how to solve problems that involve the probability of mutually exclusive, non-mutually exclusive, and complementary events.
Try This 3
Out of 150 students, 86 are writing the English diploma exam, 45 are writing the physics diploma exam, and 15 are writing both exams.
- Create Venn diagrams to represent the situation. Note: You should have four Venn diagrams when you have finished.
- Begin by creating a Venn diagram that shows the number of students who are writing both exams.
- Create a new Venn diagram that shows how many students are only writing the English diploma exam.

- Create a new Venn diagram that shows how many students are writing only the physics diploma exam.

- Finally, create a new Venn diagram that shows how many students are not writing the English or the physics exam. This will be your completed Venn diagram.
- What is the probability that a randomly chosen student is not writing the English nor the physics diploma exam?
- To the nearest hundredth, what is the probability that a randomly chosen student is writing either the English or the physics diploma exam?
- To the nearest hundredth, what is the probability that a randomly chosen student from this group is only writing the physics diploma exam?
![]() Save your responses in your course folder.
Save your responses in your course folder.
1.9. Explore 5
Module 2: Probability
In Try This 3, you identified events as mutually exclusive, non-mutually exclusive, and complementary. You solved a real-life problem that involved the probability of mutually exclusive, non-mutually exclusive, and complementary events. You will now apply this understanding in the following questions.
Self-Check 3
![]()
- Complete question 14 on page 179 of your textbook. To see how to solve this problem, view the video titled Probability—Cats and Dogs.

Pay attention to the use of the words or and and in the context of a problem.
- Complete question 3 on page 176 of your textbook. Answer
- Complete question 15 on page 179 of your textbook. Answer
- Complete “Your Turn” on page 173 of your textbook. Answer
Remember to subtract events that are being counted twice when dealing with non-mutually exclusive events.
Add the following terms to your copy of Glossary Terms:
- mutually exclusive events
- non-mutually exclusive events
Add the following to your copy of Formula Sheet:
- mutually exclusive events
P(A or B) = P(A) + P(B)
P(A ∪ B) = P(A) + P(B) - non-mutually exclusive events
P(A or B) = P(A) + P(B) − P(A and B)
P(A ∪ B) = P(A) + P(B) − P(A ∩ B)
Note: This formula can also be used for mutually exclusive events because P(A and B) will be zero.
1.10. Connect
Module 2: Probability
Complete the Lesson 2 Assignment that you saved in your course folder at the beginning of the lesson. Show work to support your answers.
![]() Save your responses in your course folder.
Save your responses in your course folder.
Project Connection
You are now ready to apply your understanding of the probability and the odds involved with mutually exclusive and non-mutually exclusive events. Go to the Module 2 Project: Carnival Probabilities. Complete the questions for Booth 1: Crazy Craps of Part 1.
1.11. Lesson 2 Summary
Module 2: Probability
Lesson 2 Summary
In this lesson you solved problems that involved mutually exclusive, non-mutually exclusive, and complementary events. You also calculated the probability associated with those events.
To summarize, imagine that you have a deck of cards. An example of a mutually exclusive event would be selecting a black jack and a red jack at the same time.

© Mannaggia/23299310/Fotolia
An example of a non-mutually exclusive event would be selecting a heart and a queen at the same time.

© Mannaggia/23299310/Fotolia
An example of an event is selecting all clubs from the deck of cards.

© Mannaggia/23299310/Fotolia
Therefore, an example of a complementary event is selecting all non-clubs from the deck of cards.

© Mannaggia/23299310/Fotolia
In the next lesson you will deal with probabilities of events that depend on each other and the probabilities of events that are independent of each other.

