Lesson 3
| Site: | MoodleHUB.ca 🍁 |
| Course: | Math 30-2 SS |
| Book: | Lesson 3 |
| Printed by: | Guest user |
| Date: | Wednesday, 24 December 2025, 12:44 PM |
Description
Created by IMSreader
1. Lesson 3
Module 2: Probability
Lesson 3: Independent and Dependent Events
Focus

Ryan McVay/Digital Vision/Thinkstock
There are many factors that can affect the outcome of a sporting event; because of this, specific rules are written for each sport. Home court advantage, travel distance, crowd size, and weather conditions are a few factors that may impact a team winning or losing.
Can you think of factors that have no bearing on the outcome of a game? In this lesson you will discover that there are some events that directly affect each other and others that are strictly independent.
Lesson Outcomes
At the end of this lesson, you will be able to
- determine if events are independent or dependent
- calculate the conditional probability of one event
- calculate the probability of two dependent or two independent events
Lesson Question
You will investigate the following question: How are problems that involve the probability of two independent or dependent events solved?
Assessment
Your assessment may be based on a combination of the following tasks:
- completion of the Lesson 3 Assignment (Download the Lesson 3 Assignment and save it in your course folder now.)
- course folder submissions from Try This and Share activities
- additions to Glossary Terms and Formula Sheet
- work under Project Connection
1.1. Discover
Module 2: Probability
Discover
Finding the probability of two events can sometimes be challenging because the outcome of the second event may depend on the outcome of the first event.
In the following Try This you will investigate different probability scenarios.
Try This 1
Open Compound Independent and Dependent Events and complete the questions that follow.
- Drag three blue and two green marbles into the bag. You will draw two marbles out by setting the “Number of Draws” to “2.” Replace the marbles after each draw by selecting “Yes.” Use a table similar to the following to record your responses.
Experiment
Outcome
Calculation
Probability
Two marbles are drawn and the first marble is replaced.
BB
BG
GB
GG
- Now conduct the same experiment, but instead each marble is not replaced in the bag after it is drawn. Record your results in a table like the following.
Experiment
Outcome
Calculation
Probability
Two marbles are drawn and the first marble is not replaced.
BB
BG
GB
GG
- What is the difference between the calculations of the probability when the marble is replaced versus when the marble is not being replaced?
![]() Save your responses in your course folder.
Save your responses in your course folder.
Share 1
Work with a partner or in a group. Complete the following.
- Discuss the pattern you found in the probability calculation when the marble is replaced and when the marble is not replaced.
- Once you have identified a pattern, try another experiment with a different number of blue and green marbles. Does the same pattern hold true when you replace the first marble and when you do not replace the first marble?
![]() If required, place a summary of your discussion in your course folder.
If required, place a summary of your discussion in your course folder.
1.2. Explore
Module 2: Probability
Explore
In Discover, you noticed the difference in probability when marbles were replaced versus when marbles were not replaced. Two events are independent if the outcome of one event has no influence on the outcome of the other event. With independent events, the number of possible outcomes remains the same throughout the experiment. Some examples of independent events include the following:
- You spin the spinner, like the one shown, twice. The result from the first spin is completely independent from the result of the second spin.

- Two cards are randomly selected from a standard deck of playing cards. After drawing the first card, it is returned to the deck. The second card is then drawn.
- Marbles are drawn from a bag and returned before the next draw.
Two events are dependent if the outcome of the first event influences the outcome of the second event. The number of possible outcomes is changed. Some examples of dependent events include the following:
- You call to make an appointment with the dentist and you select an appointment time. Your friend then calls the same dentist and selects an appointment time that is still available.
- At a fundraising event, a ticket is drawn. That ticket is awarded second prize and taped on the gift. Your ticket is still in the draw.
- Marbles are drawn from a bag and not returned before the next draw.
Watch the video “Identifying Independent Events” to see how independent or dependent events can be identified.
Self-Check 1
Complete question 1 on page 198 in your textbook. Answer
1.3. Explore 2
Module 2: Probability
For independent events, you have seen that the probability of the second event is not influenced by the probability of the first. You will now investigate how to calculate the probability of two independent events.
Try This 2
Part A
You have a fair coin, a fair die, and a spinner.



- Given the experiments in the table, calculate each probability. The first row is completed for you as a guide.
Experiment
Event A
P(A) =
Event B
P(B) =
P(A) × P(B) =
flipping a coin twice
flipping a head
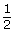
flipping a tail
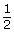
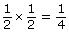
flipping a coin and rolling a die
flipping a head
rolling a six
spinning the spinner and flipping a coin
spinning a red
flipping a tail
![]() Save your responses in your course folder.
Save your responses in your course folder.
Part B
Use Exploring Probability—Explore It to check your answers in Part A. Use either the tree diagram or the chart to check the probabilities of the independent events in your table from Part A.
-
After completing the table and checking your answers using the applet, describe in your own words how you would calculate the probabilities of two independent events.
![]() Save your responses in your course folder.
Save your responses in your course folder.
1.4. Explore 3
Module 2: Probability
From Try This 3, you can summarize calculating the probability of independent events as follows:
When two events, A and B, are independent, the probability of both occuring is
![]()
The formula states that the probability of two independent events can be determined by finding the product of the two events.
Watch the video clip titled “Independent Events 2” to further understand the use of the independent events formula.
Self-Check 2
Complete questions 5.a. and 5.b. on page 198 in your textbook. Answer
1.5. Explore 4
Module 2: Probability
The probability of independent events can also be calculated by using graphic organizers such as Venn or tree diagrams.
Read “Example 2” on pages 194 to 197 of your textbook. Note how Max uses a Venn diagram to represent the problem and Melissa uses a tree diagram. Which method do you prefer?
Self-Check 3
- Complete question 6 on page 199 of your textbook. Answer
- Complete question 13 on page 200 of your textbook. Answer
- Complete question 8 on page 199 of your textbook. Answer
- A nationwide survey found that 35% of people in Canada have an electronic tablet and 68% of people in Canada have a cellphone.
- Use a graphic organizer, such as a tree diagram, to show all the possible outcomes with the corresponding probabilities. Answer
- How can you verify the probabilities for the tree diagram? Answer
- What is the probability that a person owns both a cellphone and an electronic tablet? Answer
- What is the probability that a person owns a cellphone but not an electronic tablet? Answer
- What is the probability that a person owns neither a cellphone nor an electronic tablet? Answer
1.6. Explore 5
Module 2: Probability
In Discover, you determined that in dependent events, the probability of the second event is influenced by the probability of the first event. This probability is considered to be conditional.
You can also have more than one event happening at the same time. Let’s investigate how to calculate the probability of two dependent events.
Try This 3
From Discover, you learned that when the marble was not replaced, the probability of the second event happening was directly affected and that the events were considered to be dependent. Use Compound Independent and Dependent Events to investigate how the probability of dependent events is calculated.
Start with a bag that contains three blue and four green marbles. Draw two marbles from the bag, one at a time. Each marble is not replaced in the bag after it is drawn. Then complete the activity using two blue marbles and seven green marbles in the bag. Do not replace marbles.
- Using the applet, determine the calculation to find the probability of each outcome. Record your results in a chart like the following.
Experiment
Outcome
Calculation
three blue marbles and four green marbles
BB
BG
GB
GG
two blue marbles and seven green marbles
BB
BG
GB
GG
- How does the probability that the first event will occur directly affect the probability that the second event will occur? Explain.
- Develop a general formula to find the probability for picking two blue marbles without replacing the first after it is drawn.
- Explain why the probability of the second event is considered to be conditional.
![]() Save your responses in your course folder.
Save your responses in your course folder.
Share 2
With a partner or in a group, compare the general formula that you created for question 3 of Try This 3. Come to an agreement on a general formula; then return to the applet and test the formula using a bag of two blue marbles and five green marbles.
![]() If required, save a copy of your discussion in your course folder.
If required, save a copy of your discussion in your course folder.
1.7. Explore 6
Module 2: Probability
From Try This 4, you can summarize calculating the probability of two dependent events as follows:
When two events, A and B, are dependent, the probability of both occurring is
![]()
P(B|A) is the notation for conditional probability. It should be read as “the probability of event B happening, given that event A has already occurred.”
The formula can be manipulated in the following ways:
![]()
To see how this formula is used in a real-life scenario, turn to pages 182 and 183 of your textbook. Go over “Example 1.” Pay particular attention to the tree diagram on page 182 and how the formula is used to calculate the answer on page 183.
Self-Check 4
1.8. Explore 7
Module 2: Probability

Jupiterimages/Comstock/Thinkstock
Sometimes predictions are made that involve dependent events. In board games, for example, one player’s move depends on what an opponent has done. A player might have a next move all planned out, but an opponent can foil those plans with a preceding move!
Read “Example 4” on page 186 of your textbook, and review Hillary’s solution to see how different possibilities are considered when predicting the probability of Hillary’s team winning.
Self-Check 5
- Complete “Your Turn” on page 187 of your textbook. Answer
- Complete question 6 on page 189 of your textbook. Answer
Being able to differentiate between independent and dependent events can sometimes be challenging. In the next Self-Check, you will need to identify if the events are independent or dependent before solving the problems. Using a graphic organizer, such as a chart, a tree diagram, or a Venn diagram, can be helpful to sort necessary information.
Self-Check 6
- Open the Compound Independent and Dependent Events gizmo, and complete the five “Assessment Questions” that follow the simulation. Press “Check Your Answers” to ensure you have fully understood the questions.
![]()
- Complete question 2 on page 198 of your textbook. Answer
- For Company X, expected sales are based on the strength of the economy and past statistics. For 34% of the time in a good economy, the expected sales would be $10 million. The company predicts that there is a 54% chance of a good economy this year. Determine the probability that the expected sales will be $10 million. Answer
- Complete question 11 on page 199 of your textbook. Answer
- Complete question 18 on page 201 of your textbook. Answer
Add the following terms to your copy of Glossary Terms:
- independent events
- dependent events
- conditional events
Add the following formulas to your copy of Formula Sheet:
- independent events: P(A ∩ B) = P(A) × P(B)
- dependent events: P(A ∩ B) = P(A) × P(B|A) or
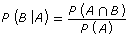
1.9. Connect
Module 2: Probability
Complete the Lesson 3 Assignment that you saved in your course folder at the beginning of the lesson. Show work to support your answers.
![]() Save your responses in your course folder.
Save your responses in your course folder.
Project Connection
You are now ready to complete your project. Go to the Module 2 Project: Carnival Probabilities. You will conclude Part 1 by completing the questions for Booth 2: Raffle Fundraiser and Booth 3: Basketball Shot. Then you will complete Part 2. Submit your project to your teacher when it is complete.
1.10. Lesson 3 Summary
Module 2: Probability
Lesson 3 Summary
In this lesson you learned how to identify events that are independent and dependent. The act of replacing or not replacing during the first event plays an important role. Once the event is identified as dependent or independent, the appropriate formula is used to solve probability problems.
You can apply independent and dependent formulas to scenarios that can affect the outcome of a game; for example, home court advantage, travel distance, crowd size, weather conditions, and other factors that may impact a team winning or losing.