Lesson 2
| Site: | MoodleHUB.ca 🍁 |
| Course: | Math 30-2 SS |
| Book: | Lesson 2 |
| Printed by: | Guest user |
| Date: | Wednesday, 24 December 2025, 7:12 PM |
Description
Created by IMSreader
1. Lesson 2
Module 3: Permutations, Combinations, and the Fundamental Counting Principle
Lesson 2: Factorial Notation
Focus

iStockphoto/Thinkstock
Sierra is playing an online game called “Win That Car!” She is presented with four virtual keys and four doors. Each key is a different colour. If she puts the correctly coloured keys into the correct doors, she wins the car. Once she has used a key, she cannot use it again. How many ways can she put the keys in the doors? ![]()
As you saw at the end of the last lesson, factorial notation is mathematical shorthand for writing out the product of consecutive natural numbers and it is used when determining the number of arrangements of objects.
Lesson Outcomes
At the end of this lesson, you will be able to
- calculate the number of arrangements of items using factorial notation
- simplify algebraic expressions involving factorials and use this in solving equations
Lesson Questions
In this lesson you will investigate the following questions:
- How many arrangements of n distinct objects are present when they are arranged into a sequence containing all n objects?
- How are algebraic expressions involving factorial notation simplified?
Assessment
Your assessment may be based on a combination of the following tasks:
- completion of the Lesson 2 Assignment (Download the Lesson 2 Assignment and save it in your course folder now.)
- course folder submissions from Try This and Share activities
- additions to Glossary Terms
- work under Project Connection
1.1. Launch
Module 3: Permutations, Combinations, and the Fundamental Counting Principle
Launch
Do you have the background knowledge and skills you need to complete this lesson successfully? Launch will help you find out.
Before beginning this lesson, you should be able to factor quadratic equations of the form ax2 + bx + c = 0, where a = 1 and where a ≠ 0.
1.2. Are You Ready?
Module 3: Permutations, Combinations, and the Fundamental Counting Principle
Are You Ready?
Complete these questions. If you experience difficulty and need help, visit Refresher or contact your teacher.
Solve each of the following equations for x.
If you answered the Are You Ready? questions without difficulty, move to Discover.
If you found the Are You Ready? questions difficult, complete Refresher.
1.3. Refresher
Module 3: Permutations, Combinations, and the Fundamental Counting Principle
Refresher
The video “Factoring Trinomials with a Leading 1 Coefficient” describes how to factor a trinomial with a leading 1.
The video “Factoring Trinomials with a non-1 Leading Coefficient by Grouping” describes how to factor a trinomial with a non-1 leading coefficient.
The videos “Solving Quadratic Equations by Factoring” and “Solving Quadratic Equations by Factoring 2” both describe how to solve a quadratic equation by factoring.
Go back to the Are You Ready? section and try the questions again. If you are still having difficulty, contact your teacher.
1.4. Discover
Module 3: Permutations, Combinations, and the Fundamental Counting Principle
Discover
You have seen that 10! = 10 × 9 × 8 × 7 × 6 × 5 × 4 × 3 × 2 × 1.
If you let n = 10, then the preceding expression can be written as follows:
n! = n × (n − 1) × (n − 2) × (n − 3) × (n − 4) × (n − 5) × (n − 6) × (n − 7) × (n − 8) × (n − 9)
or
n! = n(n − 1)(n − 2)(n − 3 )…(3)(2)(1)
It is important to note that n! is only defined when n is a natural number.
Calculating the value of an expression involving factorial notation without a calculator can be a time-consuming process. In the following Try This, you will look for patterns that might exist between subsequent expressions involving factorial notation.
Try This 1
- Complete a chart like the following. Read the hint provided in the second row if you need help.
n!
n! in Expanded Form
Expression Involving n and
(n − 1)!Value of n!
1!
1
1
1
2!
2 × 1
2 × _!


2
3!
3 × 2 × 1
3 × _!


4!
_ × _ × _ × _

4 × _!


5!
_ × _ × _ × _ × _

5 × _!


6!
_ × _ × _ × _ × _ × _

6 × _!


7!
_ × _ × _ × _ × _ × _ × _

7 × _!


- Describe the relationship between n! and (n − 1)!.
- Create a general expression relating n!, n, and (n − 1)!.
![]() Save your responses in your course folder.
Save your responses in your course folder.
1.5. Explore
Module 3: Permutations, Combinations, and the Fundamental Counting Principle
Explore
In Try This 1, you discovered that n! can be written several ways. One general expression you may have found is n! = n(n − 1)!. In the following Try This, you will see some other ways to write n!.
Try This 2
Most scientific calculators have a factorial key that will calculate the product of the consecutive natural numbers beginning with the number entered. Simply enter the number and press the ! key. Some graphing calculators do not have a factorial key but have the factorial function listed within the menu system. You may need to consult your calculator instructions or your teacher to find where the ! function is located.
- Using your calculator, evaluate the following expressions.
- 6!
- 6 × 5!
- 6 × 5 × 4!
- What do you notice about your answers for questions 1.a., b., and c.?

![]() Save your responses in your course folder.
Save your responses in your course folder.
Self-Check 1
-
Rewrite 12! in two different forms. AnswerDid You Know?
Most calculators will have a factorial key, and usually the largest value that can be calculated is 69!. Try 69! in your calculator, and see what happens when you try to enter 70!. - Rewrite 7 × 6 × 5! in two different forms. Answer
There are times when it is necessary to simplify factorial expressions. You will explore one way in the next Try This.
Try This 3
Find the value of ![]() .
.
- Expand the numerator to show all the factors in 12!.
- Expand the denominator to show all the factors in 9!.
- Divide the numerator and denominator by any common factors.
- Calculate the solution by multiplying the remaining factors.
![]() Save your responses in your course folder.
Save your responses in your course folder.
1.6. Explore 2
Module 3: Permutations, Combinations, and the Fundamental Counting Principle
As you may have noticed in Try This 3, writing out all the factors can take a long time. Here is another way you could simplify ![]() .
.
Expanding the numerator and denominator gives you the following:
![]()
As you can see, the expression in the brackets is the same as 9!; therefore, you can write ![]() as
as ![]()
Dividing numerator and denominator by the common factor of 9! leaves 12 × 11 × 10 or 1320.
Self-Check 2
![]()
- Complete questions 1.a., 1.c., 1.f., 3.c., 4, 5.a., 5.c., and 5.e. on pages 81 and 82 of your textbook. Answer
1.7. Explore 3
Module 3: Permutations, Combinations, and the Fundamental Counting Principle
Remember that factorial notation is mathematical shorthand for the product of consecutive descending natural numbers.
Try This 4
- Expand 9!.
- Expand (n + 1)!.

- How does what you did in questions 1 and 2 relate to the definition n! = n(n − 1)(n − 2)(n − 3)…(3)(2)(1)?
![]() Save your responses in your course folder.
Save your responses in your course folder.
1.8. Explore 4
Module 3: Permutations, Combinations, and the Fundamental Counting Principle
In Try This 4, you practised expanding a factorial expression that included the variable n. The ability to expand factorial expressions helps to simply expressions.
Simplify ![]()
Expand both the numerator and denominator.
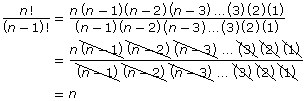
The only factor that did not divide out of the numerator and denominator was the n.
Read “Example 3” on page 79 of your textbook. Notice how the product in part a can be simplified as a single factorial expression.
Self-Check 3
1.9. Explore 5
Module 3: Permutations, Combinations, and the Fundamental Counting Principle
In Self-Check 3, you simplified algebraic fractions involving factorial notation by dividing the numerator and the denominator by the same factors. For example,
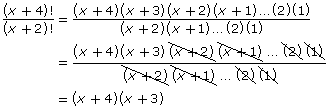
or
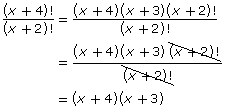
In a similar fashion, expressions with factorials can be simplified to solve equations.
Solving a Factorial Equation will show you how to simplify an expression that includes factorials in order to solve an equation.
If you would like to review another example of how to solve an equation that involves factorial notation, read “Example 4” on page 80 of your textbook.
Self-Check 4
1.10. Explore 6
Module 3: Permutations, Combinations, and the Fundamental Counting Principle
permutation: an arrangement of distinguishable objects in a definite order
For example, the objects a and b have two permutations, ab and ba.1
In the previous lesson you examined the number of ways 10 children could be lined up for recess. You discovered that the total number of ways, using factorial notation, was 10! or 3 628 800. The number of arrangements, also known as permutations, of 10 objects is 10!.
In general, you can say the number of permutations of n items is n! where n! = n(n − 1)(n − 2)(n − 3)…(3)(2)(1). The questions you have solved in this lesson and Lesson 1, where you calculated the number of arrangements of items, are also known as determining the number of permutations.

Stockbyte/Thinkstock
Permutation questions involve order. A, B, C would be considered a different permutation from B, C, A.
Consider the following example: A baseball coach is setting his batting line-up. Assuming all nine players can hit in any place in the line-up, in how many ways can the coach choose his line-up?

Digital Vision/Thinkstock
The coach has nine players to choose from for the first spot in the line-up. Once the coach has chosen a name to write down in the first place in the line-up, there are eight names to choose from for the second place in the line-up. Once a second name has been chosen, the coach then has seven names to choose from, and so on. This is a permutation question involving order, and factorial notation can be used to solve it.
9 × 8 × 7 × 6 ×… and so on can be written
as 9! = 362 880
What would happen to the number of permutations if the baseball coach wanted to put Sarah last in his batting line-up because the coach knew she was going to be late for the game? The other spots could be filled in any order.
In this case, the final spot would be filled in with Sarah’s name. There is only one way to fill in this last spot. That leaves the coach with eight more spots in the line-up to fill in with the eight other names. The coach has eight names to choose from for the first spot, seven names to choose from for the second spot, and so on.
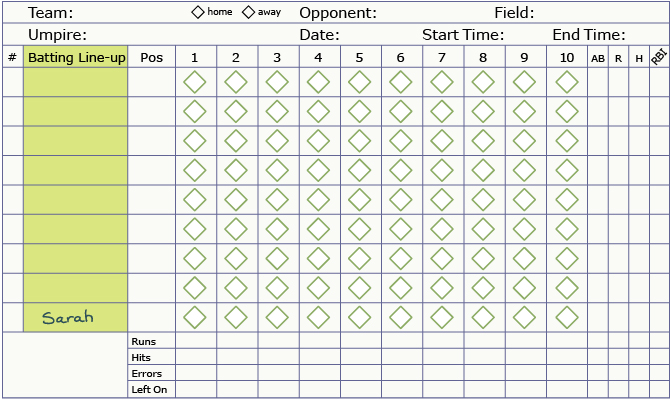
The solution can be written as follows:
![]()
This is equal to 8! or 40 320.
Self-Check 5
Add the following terms to your copy of Glossary Terms:
- permutation
- factorial
For each new definition in your glossary, be sure to include the appropriate notation.
1 From PRINCIPLES OF MATHEMATICS 12 by Canavan-McGrath et al. Copyright Nelson Education Ltd. Reprinted with permission.
1.11. Connect
Module 3: Permutations, Combinations, and the Fundamental Counting Principle
Complete the Lesson 2 Assignment that you saved in your course folder at the beginning of the lesson. Show work to support your answers.
![]() Save your responses in your course folder.
Save your responses in your course folder.
Project Connection
You are now ready to apply your understanding of the factorial notation and the fundamental counting principle. Go to Part 1 of Module 3 Project: Math Mystery. Complete Activity 1 in the Elite Math Code Breakers multimedia piece. Make sure to save all your answers and solutions to these questions in your course folder.
1.12. Lesson 2 Summary
Module 3: Permutations, Combinations, and the Fundamental Counting Principle
Lesson 2 Summary
In this lesson you learned how to simplify expressions involving factorial notation and how to solve equations that contained factorial expressions. You learned that permutations are questions in which order is important and that solving these questions may involve the use of factorial notation. You learned the importance of order in security measures such as codes, passwords, and some types of locks.
In the next lesson you will learn how to apply these skills in determining the number of permutations of n items taken r at a time. For example, this means you may have 10 items and be asked to select only 6 of those items at a time. In this lesson you selected all items each time (i.e., n items taken n at a time).




