Lesson 4
| Site: | MoodleHUB.ca 🍁 |
| Course: | Math 30-2 SS |
| Book: | Lesson 4 |
| Printed by: | Guest user |
| Date: | Wednesday, 24 December 2025, 7:13 PM |
Description
Created by IMSreader
1. Lesson 4
Module 3: Permutations, Combinations, and the Fundamental Counting Principle
Lesson 4: Solving Problems That Involve Combinations
Focus

iStockphoto/Thinkstock
In his book The Codebreakers: The Story of Secret Writing, David Kahn tells the story of how a New York City detective broke up a betting ring. The detective observed a bookie taking bets all day and writing them down. However, when the detective made the arrest, much to his surprise, the list did not consist of names and amounts of bets but rather a series of musical notes. Convinced that the notes must be a code, the detective took the list for cryptanalysis. Sure enough, when the notes were played it did not result in beautiful music. Indeed, the notes were a code! The detective broke the code and solved his case.
There have been cases of music notes being used to deliver hidden messages. The code might be in the music lyrics or within the notes themselves.
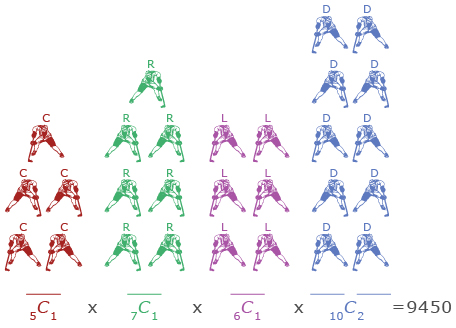
The piano is one of the most common musical instruments in the world. A typical keyboard has 88 keys with a repetitive naming sequence as shown in the diagram. Keys with the same name, such as two A notes, sound similar, but one note is higher than the other.
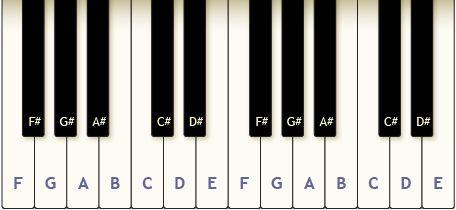
This illustration shows part of a piano keyboard.
A chord can be produced on a piano when more than one key is pressed at the same time. How could you determine the number of different chords a piano can produce? What if you wanted chords using only the white keys? Suppose the pianist’s fingers could only span eight white keys. How could you determine how many one-handed chords could be produced?
In the previous lesson you examined permutations—that is, the number of ways objects can be arranged when order is important. But on the piano, the order a chord is written in or played does not change its sound. ACE is the same as CAE since all keys are pressed at the same time in a chord.
In this lesson you will explore a method of determining the number of ways to select objects if the order is not important.
Lesson Outcome
At the end of this lesson, you will be able to determine the number of combinations of elements given certain criteria.
Lesson Questions
In this lesson you will investigate the following questions:
- What are the similarities and differences between permutation and combination problems?
- How are problems involving combinations solved?
Assessment
Your assessment may be based on a combination of the following tasks:
- completion of the Lesson 4 Assignment (Download the Lesson 4 Assignment and save it in your course folder now.)
- course folder submissions from Try This and Share activities
- additions to Glossary Terms and Formula Sheet
- work under Project Connection
1.1. Launch
Module 3: Permutations, Combinations, and the Fundamental Counting Principle
Launch
Do you have the background knowledge and skills you need to complete this lesson successfully? Launch will help you find out.
Before beginning this lesson, you should be able to
- determine the number of permutations of a specified number of items under certain conditions
- simplify expressions involving factorial notation
1.2. Are You Ready?
Module 3: Permutations, Combinations, and the Fundamental Counting Principle
Are You Ready?
Complete these questions. If you experience difficulty and need help, visit Refresher or contact your teacher.
- Simplify
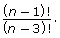 Answer
Answer - Solve the equation
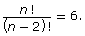 Answer
Answer - Evaluate 12P4. Answer
-
A hamburger restaurant offers the following choices:
- 3 types of buns
- 4 types of burger patties
- 5 types of toppings
- 4 types of condiments
If Breanna wants a burger with one item from each category, how many different burgers can she choose from? Answer
- Landon and Byron are roommates, and together they have a total of 22 hats. If they both want to choose a hat from their collection, how many different ways can they select their hats? Answer
If you answered the Are You Ready? questions without difficulty, move to Discover.
If you found the Are You Ready? questions difficult, complete Refresher.
1.3. Refresher
Module 3: Permutations, Combinations, and the Fundamental Counting Principle
Refresher
Watch the video “Permutations” that provides several solved examples of permutations and factorial notation.
Go back to the Are You Ready? section and try the questions again. If you are still having difficulties, contact your teacher.
1.4. Discover
Module 3: Permutations, Combinations, and the Fundamental Counting Principle
Discover
Try This 1
Suppose you are planning to open an ice cream stand and have 4 kinds of ice cream: chocolate, vanilla, strawberry, and tiger (licorice). You plan to serve 2 different scoops at a time. Use the interactive piece titled Two Scoops to determine how many 2-flavour cones can be made.
- If you wanted to advertise the number of different 2-flavour cones available, would you calculate the number available by using 4P2 = 12? Explain.
- If you added another flavour—blueberry—how many different cones could you produce?
![]() Save your responses in your course folder.
Save your responses in your course folder.
Share 1
With a partner or group, discuss the following questions based on what you discovered in Try This 1.
- What do you suppose the 4 and the 2 represent in 4C2 from the interactive Two Scoops if the C stands for combination?
- Describe another scenario where you might use combinations (i.e., arrangements where order doesn’t matter) instead of permutations.
![]() If required, save a copy of your discussion in your course folder.
If required, save a copy of your discussion in your course folder.
1.5. Explore
Module 3: Permutations, Combinations, and the Fundamental Counting Principle
Explore
In Try This 1, you looked at permutations and combinations of ice cream cones. The number of combinations is the number of ways you can select items from a group when order does not matter. In the Two Scoops interactive, a chocolate-strawberry cone is the same as a strawberry-chocolate cone.
You may have noticed in Discover that the notation for combinations is similar to that of permutations.
|
Notation |
Order |
Ice Cream Cone Possibilities |
Combination |
nCr |
order does not matter |
4C2 = 6 |
Permutation |
nPr |
order matters |
4P2 = 12 |
In Try This 1, nCr represents taking r objects (2 flavours) from a group of n (4 possible flavours) when the order does not matter. In nPr, the restriction on r is r ≤ n. This is also true for nCr because you can’t choose more objects than are available.
In the following Try This 2, you will explore combinations and how they compare to permutations.
Try This 2
Step 1: Open the Permutations and Combinations gizmo from LearnAlberta.
Screenshot reprinted with permission of ExploreLearning
This gizmo represents the number of ways you can take items from a box. It also allows you to decide whether to pay attention to the order or not. This is an added feature as compared to the gizmo you used in Lesson 3.
Step 2: Set “Number of tiles in box” to 3.
Step 3: Set “Number of draws from box” to 2, and select “Yes” to indicate that the order is important. This setting corresponds to the first line of the table you will complete in step 5.
Step 4: Choose “Simulate.” Switch between the tabs at the top for different representations of the information.

Screenshot reprinted with permission of ExploreLearning
Step 5: Complete the following table.
Tiles |
Draws |
Is Order Important? |
Number of Possibilities |
Sketch of Tree Diagram |
Notation |
Permutation or Combination |
3 |
2 |
Yes |
6 |
|
3P2 |
Permutation |
3 |
2 |
No |
|
|
|
|
5 |
2 |
Yes |
|
|
|
|
5 |
2 |
No |
|
Do not draw. |
|
|
4 |
3 |
No |
|
Do not draw. |
|
|
4 |
4 |
No |
|
Do not draw. |
|
|
5 |
5 |
No |
|
Do not draw. |
|
|
![]() Save your answers to your course folder.
Save your answers to your course folder.
Share 2
With a partner or group, discuss the following questions based on what you discovered in Try This 2.
- How did the tree diagram change when you switched from order being important to not important?
- Why are there fewer combinations of a specified number of items as compared to the number of permutations?
- The interactive shows that the permutation and combination formulas are related by
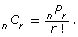 Explain why dividing the number of permutations by r! gives the number of combinations.
Explain why dividing the number of permutations by r! gives the number of combinations. - Think of a real-life example where you would be interested in the number of combinations instead of permutations.
![]() If required, save a record of your discussion in your course folder.
If required, save a record of your discussion in your course folder.
1.6. Explore 2
Module 3: Permutations, Combinations, and the Fundamental Counting Principle
In the Permutations and Combinations gizmo, you may have noticed you could represent the number of combinations 5C3 as ![]() The number of combinations, nCr, is equal to the number of permutations, nPr, divided by the number of ways the elements could be arranged, r!.
The number of combinations, nCr, is equal to the number of permutations, nPr, divided by the number of ways the elements could be arranged, r!.
In the Two Scoops example, you saw 2!, or 2, duplicates for each cone, so there were twice as many permutations as combinations. So to find the combinations, divide nPr by 2! in order to remove the duplicates.
Your calculator likely has a nCr button that will calculate the number of combinations for you. Note that some textbooks use an alternate notation for combinations ![]() where
where ![]()
For the previous ice cream example, you could write ![]() and know this meant 4C2. You evaluated this and got 6. The combination function on your calculator will likely be found in the same menu as the permutation function. Make sure you can use your calculator to evaluate this. Check with your teacher if you have trouble finding this function.
and know this meant 4C2. You evaluated this and got 6. The combination function on your calculator will likely be found in the same menu as the permutation function. Make sure you can use your calculator to evaluate this. Check with your teacher if you have trouble finding this function.
Self-Check 1

Brand X Pictures/Thinkstock
A Grade 12 class of 120 students is forming a graduation committee.
1.7. Explore 3
Module 3: Permutations, Combinations, and the Fundamental Counting Principle
So far, you have seen that ![]() can be used to determine the number of combinations. It is also possible to rewrite this formula without the permutation component.
can be used to determine the number of combinations. It is also possible to rewrite this formula without the permutation component.
|
|
|
So it is easier to visualize, rewrite the division by r! as the multiplication by |
|
Since you know that nPr can be written as |
|
Multiply. |
So the combination formula is as follows:
![]()

Brand X Pictures/Thinkstock
Read “Example 2” on page 113 of your textbook. Notice how 10! is rewritten in the numerator as 10 × 9 × 8 × 7! so that the common factor, 7!, can be divided out of both the numerator and denominator.
Self-Check 2
- Complete “Your Turn” on the bottom of page 113 of your textbook. Answer
- In how many ways can a coach choose a starting line-up of 5 basketball players if there are 15 players on the team? Answer

iStockphoto/Thinkstock
Have you ever had a combination lock given to you for a locker at school? Is this an appropriate name for this item? The word combination implies that order is not important. You know, however, that if the numbers are not done in the right order with the correct rotation in between, the lock will not unlock. So perhaps it should be called a permutation lock.
1.8. Explore 4
Module 3: Permutations, Combinations, and the Fundamental Counting Principle
As with permutations, there are often extra conditions placed on the choices to be made. For instance, in question 2 of Self-Check 2, the basketball coach could create a line-up comprised of any 15 players. But not all players can play all positions. It’s unlikely that a centre would play guard, for example. If the coach had to make choices based on positions, then the number of combinations would change. Consider the following scenario.

Ron Chapple Studios/Thinkstock
Try This 3
A hockey coach wishes to choose her first line. She has 5 centres from which she must choose one, 7 right-wingers from which she must choose one, 6 left-wingers from which she must choose one, and 10 defensemen from which she must choose two. In how many ways can the coach choose her first line?
Use a table similar to the following to help solve the problem.
|
POSITION |
|
|||
Centre |
Right-wing |
Left-wing |
Defense |
||
Number of Players to Choose From |
5 |
7 |
6 |
10 |
|
Number on Ice at One Time |
1 |
1 |
1 |
2 |
|
Combination Notation |
|
|
|
|
|
Number of Ways to Fill Each Position |
|
|
|
|
|
Total Number of Ways |
|
|
|
|
|
![]() Save your answers to your course folder.
Save your answers to your course folder.
1.9. Explore 5
Module 3: Permutations, Combinations, and the Fundamental Counting Principle
Hemera/Thinkstock
In Try This 3, the coach must choose a centre and a right-winger and a left-winger and 2 defensemen. By using the fundamental counting principle, you multiply the number of choices for each position to determine the total number of ways to make these choices.
- centre: 5C1 = 5
- right-winger: 7C1 = 7
- left-winger: 6C1 = 6
- two defensemen: 10C2 = 45
The total number of ways the coach can choose the first line is 5 × 7 × 6 × 45 = 9450 ways.
If you would like to see another example of a permutation question with extra conditions placed on it, read part b of “Example 3” on pages 114 and 115 of your textbook. As you read, note how the word and indicates that the two combinations must be multiplied to find the total number of combinations.
Self-Check 3
- Complete question 12 on page 119 of your textbook. Answer
- The student activities committee consists of 5 students from Grade 10, 5 students from Grade 11, and 8 students from Grade 12. There are also 2 teachers on the committee. How many dance subcommittees can be formed if there must be 2 students from each grade and 1 teacher? Answer
1.10. Explore 6
Module 3: Permutations, Combinations, and the Fundamental Counting Principle

AbleStock.com/Thinkstock
Remember that in some of the permutation calculations in Lesson 3, you used cases. Cases can be used to split a solution into different possible scenarios. Because you can have the first scenario or the second scenario, you add the number of permutations in each case to determine the total. There are also some combination questions that require the use of cases. Consider the following example.
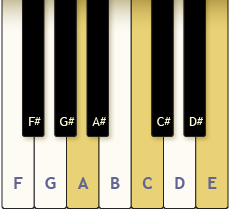
Pianists can create different chords by pressing several keys down at the same time on a piano.
How many chords are possible in each situation?
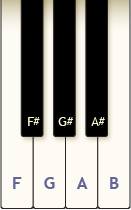
- Using the keys from the piano as shown, how many different chords—combinations of two or more keys—can be produced using exactly 4 fingers if each finger only presses 1 key, black or white, at a time?
- How many chords can be produced using 3 or 4 fingers?
- How many chords can be produced using 2 or 3 or 4 fingers?
Watch Piano Chords to see how the number of chords can be calculated for each situation.
1.11. Explore 7
Module 3: Permutations, Combinations, and the Fundamental Counting Principle
To see another example of solving a combination problem by considering cases, read “Example 4” on page 116 of your textbook. As you read, think about when it would be more efficient to use indirect reasoning rather than direct reasoning.
Self-Check 4
- Complete “Your Turn” on the top of page 117. In your answer, note when you would use indirect reasoning over direct reasoning. Answer
- There are 8 boys and 5 girls in the debate club. A team of 5 students must be chosen for a competition. There must be at least 2 boys selected.
1.12. Explore 8
Module 3: Permutations, Combinations, and the Fundamental Counting Principle
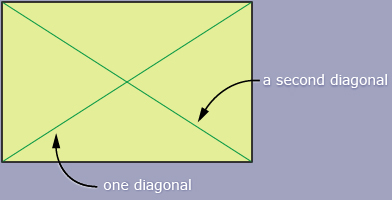
Diagonals are line segments that join two non-adjacent vertices in a polygon. For example, a quadrilateral (four-sided shape) will have two diagonals.
Can you use your math skills from this unit to find the number of line segments in any polygon? Perhaps you can find the number of line segments if you include both sides and diagonals?
If you have a quadrilateral showing diagonals and want to know the total number of line segments, you could draw a picture showing the line segments and count them. Since you have 4 sides and 2 diagonals, you have a total of 6 line segments.
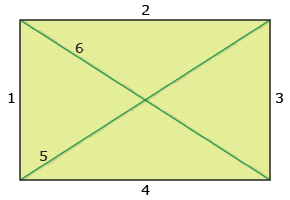
Can you use permutations or combinations to find this same answer of 6? Since you have 4 vertices and you connect 2 of them at a time, would either expression 4P2 or 4C2 be the correct answer?
![]()
You see that the combination formula results in the correct answer. This makes sense since the order you choose the vertices will not change the look of the line segment. Therefore, order is not important.
Self-Check 5
Determine the number of line segments in a pentagon, a five-sided shape. Try using the combination formula, and then draw it out to check your work. Answer
1.13. Explore 9
Module 3: Permutations, Combinations, and the Fundamental Counting Principle
To find the number of diagonals, subtract the number of sides from the total number of line segments since sides do not qualify as diagonals.
This can be represented using the following formula:
number of diagonals = nC2 − n
Self-Check 6
Complete questions 1, 6, 9, 10, 12, 15.a., and 15.c. from pages 118 and 119 of your textbook. Answer
Add combination to your copy of Glossary Terms.
Add the following formula to your copy of Formula Sheet.
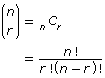
1.14. Connect
Module 3: Permutations, Combinations, and the Fundamental Counting Principle
Complete the Lesson 4 Assignment that you saved in your course folder at the beginning of the lesson. Show work to support your answers.
![]() Save your responses in your course folder.
Save your responses in your course folder.
Project Connection
You are now ready to apply your understanding of combinations. Go to Part 1 of Module 3 Project: Math Mystery. Complete Activity 3 in the Elite Math Code Breakers multimedia piece. Make sure to save all your answers and solutions to these questions in your course folder.
1.15. Lesson 4 Summary
Module 3: Permutations, Combinations, and the Fundamental Counting Principle
Lesson 4 Summary
Combinations can be used to solve counting problems where the order is not important. A combination can be represented by nCr or ![]() where n is the size of the group from which the objects are taken and r is the number of objects that are taken at a time. The formula
where n is the size of the group from which the objects are taken and r is the number of objects that are taken at a time. The formula ![]() can be used to calculate a combination where 0 ≤ n ≤ r. Many problems will require you to calculate multiple combinations and apply the fundamental counting principle.
can be used to calculate a combination where 0 ≤ n ≤ r. Many problems will require you to calculate multiple combinations and apply the fundamental counting principle.
In Lesson 5 you will use permutations and combinations to model and solve problems.



