Lesson 5
| Site: | MoodleHUB.ca 🍁 |
| Course: | Math 30-2 SS |
| Book: | Lesson 5 |
| Printed by: | Guest user |
| Date: | Wednesday, 24 December 2025, 4:56 PM |
Description
Created by IMSreader
1. Lesson 5
Module 3: Permutations, Combinations, and the Fundamental Counting Principle
Lesson 5: Solving Probability Problems That Involve Permutations and Combinations
Focus
The pigpen cipher is a geometric substitution cipher in which symbols are substituted for letters. The symbols are derived from fragments of two tic-tac-toe boards and two X's as shown.
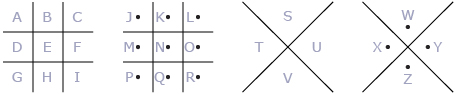
Using the pigpen cipher, the phrase “x marks the spot” would look like the following:

How could you determine the probability of someone guessing a coded message? Suppose you had some understanding of how the cipher worked. How would that change the probability of guessing correctly? Is order important when decoding a message?
Calculating the probabilities of more complex questions can often be assisted by permutations and combinations. Both can be used to help determine the number of favourable outcomes and the number of total outcomes.

photo: Courtesy of the Department of National Defence; frame: Photodisc/Thinkstock
This photograph shows Sgt. Tommy Prince, one of the most decorated Aboriginal Canadians to serve in the army during
World War II. He was a paratrooper who belonged to the First Special Service Force.
On September 10, 1939, Canadians found themselves in conflict again as our country declared war on Germany and entered the Second World War. Once again, Canada’s Aboriginal men and women answered the call of duty. By March 1940, more than 100 had volunteered and by the end of the war in 1945, more than 3,000 status Indians, as well as an unknown number of Inuit, Métis and First Nations peoples had enlisted.
One interesting role some Aboriginal Canadians would play in this conflict would be as “code talkers.” Soldiers . . . would translate sensitive messages into Cree so the enemy could not understand any intercepted transmissions. Once the message was received by another Cree-speaking “code talker,” it would be translated back into English so it could be understood by the recipients.
Source: Aboriginal Veterans, (Ottawa: Veterans Affairs Canada, 2011),
<http://www.veterans.gc.ca/eng/history/aboriginal-pi>; (24 February 2012).
Lesson Outcome
At the end of this lesson, you will be able to determine the probability of events involving permutations and combinations.
Lesson Question
In this lesson you will investigate the following question: What strategies can be used to solve probability problems that involve permutations and combinations?
Assessment
Your assessment may be based on a combination of the following tasks:
- completion of the Lesson 5 Assignment (Download the Lesson 5 Assignment and save it in your course folder now.)
- course folder submissions from Try This and Share activities
- work under Project Connection
1.1. Launch
Module 3: Permutations, Combinations, and the Fundamental Counting Principle
Launch
Do you have the background knowledge and skills you need to complete this lesson successfully? Launch will help you find out.
Before beginning this lesson, you should be able to solve probability and odds problems that do not require the use of permutations or combinations.
1.2. Are You Ready?
Module 3: Permutations, Combinations, and the Fundamental Counting Principle
Are You Ready?
Complete these questions. If you experience difficulty and need help, visit Refresher or contact your teacher.
- Determine the probability of drawing a club from a standard deck of cards. Answer
- Calculate the odds for a 1 or a 4 being rolled on a die. Answer
If you answered the Are You Ready? questions without difficulty, move to Discover.
If you found the Are You Ready? questions difficult, complete Refresher.
1.3. Refresher
Module 3: Permutations, Combinations, and the Fundamental Counting Principle
Refresher
Go to Probability (of an Event) at the Mathematics Glossary for a review of the definition of probability.
The video titled “Probability (Part 2)” demonstrates how to calculate probabilities.
For a review of odds, read Module 2: Lesson 1 of Mathematics 30-2.
Go back to the Are You Ready? section and try the questions again. If you are still having difficulties, contact your teacher.
1.4. Discover
Module 3: Permutations, Combinations, and the Fundamental Counting Principle
Discover
In Module 2 you learned that the probability of any event =
![]()
Determining the number of events often involves the use of the fundamental counting principle, permutations, and/or combinations.
Try This 1
It is possible to find different types of name generators online. Typically, word patterns are used to generate a reasonable sounding name. Consider the following superhero name generator. The superhero name becomes the _____A_____ ______B_____ _____C_____, where A, B, and C are words chosen randomly from the following lists.
| A | B | C |
Amazing |
Atomic |
Admiral |
- How many three-word names can be made from the table?
- Pick a superhero name that matches your personality. What is the probability that a three-word name picked at random will match your name?

- What is the probability that a name, picked at random, will have an animal as the second word?
- What is the probability that a random new name will have the initials G. S. W.?

![]() Save your responses in your course folder.
Save your responses in your course folder.
Share 1
With a partner or group, discuss the following questions based on what you discovered in Try This 1.
- How do your strategies for determining the number of possible names compare?
- Did you use the same strategy to solve Try This 1 question 4? What other strategies could you use?
![]() If required, save a record of your discussion in your course folder.
If required, save a record of your discussion in your course folder.
1.5. Explore
Module 3: Permutations, Combinations, and the Fundamental Counting Principle
Explore

Jupiterimages/ Polka Dot
/Thinkstock
In Try This 1, you may have found that using the fundamental counting principle and permutations helped to simplify probability calculations. There are many situations where this is the case.
Suppose you have a library of 10 country and 17 rock songs on an MP3 player. If 5 songs are picked at random, what is the probability of making a 5-song playlist with only rock music?
In this example, a favourable outcome is a playlist with 5 rock songs. The total outcomes are all the possible 5-song playlists. If you change the order of songs, you get a different playlist. Order is important, so use permutations.
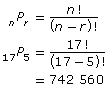 |
Determine the number of 5-song playlists containing only rock songs. In the equation, n is the total number of rock songs, and r is the number of rock songs. |
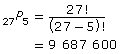 |
Determine the total number of 5-song playlists possible. In the equation, n is the total number of songs, and r is the number of songs in the playlist. |
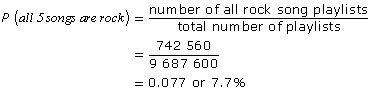 |
Determine the probability of the 5-song playlist containing 5 rock songs. |
Depending on the scenario, combinations may also prove useful when determining probabilities. You may also need to use the probability rules for the words and and or that you learned in Module 2.
Try This 2

Ryan McVay/Digital Vision/Thinkstock
Using the playlist example as a guide, solve the following problems.
A winter carnival committee of 6 people needs to be selected from 8 boys and 10 girls.
- Complete the following to determine the probability that the committee will have 3 boys and 3 girls.
- Is order important for this problem? Explain.
- Determine the number of favourable outcomes. This is the number of ways of choosing 3 boys from 8 boys and 3 girls from 10 girls.
- Determine the number of total outcomes. This is the number of ways of choosing 6 people from 18 people.
- Determine the probability of 3 boys and 3 girls by dividing the number of favourable outcomes by the total number of outcomes.
-
- What information will be required to calculate the probability that at least 2 members are girls?
- Calculate the probability that at least 2 members are girls.
- What information will be required to calculate the probability that at least 2 members are girls?
![]() Save your responses in your course folder.
Save your responses in your course folder.
1.6. Explore 2
Module 3: Permutations, Combinations, and the Fundamental Counting Principle
You may have found that the questions in Try This 2 could be solved in a similar method to those of the playlist example; however, the number of favourable outcomes in Try This 2 was a bit more complex. Read the following solutions and compare them to your solution.
A winter carnival committee of 6 people needs to be selected from 8 boys and 10 girls.
- Complete the following to determine the probability that the committee will have 3 boys and 3 girls.
First, you were asked to explain if order is important for this question. Order is not important because the positions on the committee are indistinguishable. You can use a process similar to the one shown in the MP3 playlist example. Find the number of favourable outcomes divided by the total number of outcomes.
Then, you were asked to answer a series of questions about outcomes. Following are the solutions.
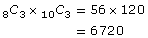
Determine the number of favourable outcomes.
This is the number of ways of choosing 3 boys from 8 boys and 3 girls from 10 girls.
18C6 = 18 564
Determine the number of total outcomes.
This is the number of ways of choosing 6 people from 18 people.
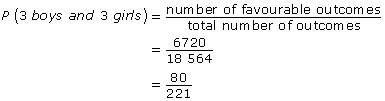
Determine the probability of 3 boys and 3 girls by dividing the number of favourable outcomes by the total number of outcomes.
-

When representing an answer for a probability question, there are three possible ways to write the answer: as a fraction in lowest terms, as a decimal, or as a percentage. So, the answer of
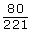 could also be written as 0.362 (rounded) or 36.2%.
could also be written as 0.362 (rounded) or 36.2%.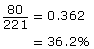
-
What information will be required to calculate the probability that at least 2 members are girls?
To calculate the probability that at least two members are girls, you need to know the total number of possible committees and the number of committees that include at least 2 girls. - Calculate the probability that at least 2 members are girls.
You can solve this using direct reasoning or indirect reasoning.
Method 1: Direct Reasoning
To use direct reasoning, find the total number of different committees that have at least 2 girls and then divide by the total number of committees.
At least 2 girls means there could be 4 boys and 2 girls or 3 boys and 3 girls or 2 boys and 4 girls or 1 boy and 5 girls or 0 boys and 6 girls.
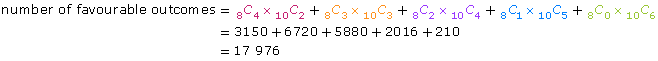
The total number of outcomes is 18C6 = 18 564.
Many calculators include a fraction command that will convert a decimal to a fraction in lowest terms. This command can be used to reduce fractions. To do this, divide the fraction to convert it to a decimal. Use the fraction command to convert it back to a fraction, but now in lowest terms.
You may need to reference your calculator manual or contact your teacher to find out where the fraction command is located on your calculator.
Try using this strategy to simplify the fraction from the problem. You should be able to show
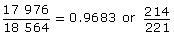
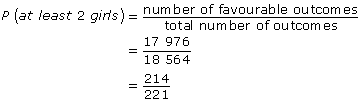
The probability that there will be at least 2 girls on the committee is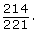
Method 2: Indirect Reasoning
To use indirect reasoning, find the probability of the complement of at least 2 girls and then subtract from 1. This means you find the probability the committee has 0 girls or 1 girl and then subtract this probability from 1.
View the multimedia piece titled Indirect Reasoning to see how Method 2 is used to solve the problem.
Image: iStockphoto/Thinkstock
-
What information will be required to calculate the probability that at least 2 members are girls?
Self-Check 1
- A class of 17 boys and 13 girls is travelling on a bus.
![]()
- Complete questions 2, 3, 5, 8, and 9 from pages 159 and 160 of your textbook. Answer
1.7. Explore 3
Module 3: Permutations, Combinations, and the Fundamental Counting Principle
So far, you have seen that probabilities can be calculated using permutations and combinations. It is important to choose whether to use permutations or combinations correctly. Complete Try This 3 to explore this idea.
Try This 3

Hemera/Thinkstock
Nine-ball is a pocket billiard game that uses balls numbered from 1 to 9 and a white cue ball. The object of the game is to sink the ball labelled 9 into a pocket. Each time a player shoots, the cue ball must strike the lowest numbered ball on the table first. Once the 9 is sunk, the game ends—even if other balls are still on the table.
Ignore the cue ball (white ball) for the following questions.
- This photo shows how the balls are aligned or “racked” before the game begins.
Hemera/Thinkstock
Suppose the balls are racked at random and you want to determine the probability that they will be in the arrangement shown in the picture.- Can you use permutations to solve the problem? Explain.
- Can you use combinations to solve the problem? Explain.
- Calculate the probability. Note: Completing a chart similar to the following may help you calculate the probability.
Solution Description Decide if order is important for this question. Determine the number of favourable outcomes. Determine the number of total outcomes. Determine the probability.
- To set up the balls properly, the 1 must be at the front and the 9 must be at the centre as shown in the picture for question 1. Suppose the balls are aligned at random and you want to determine the probability the rack will be a useable setup.
- Can you use permutations to solve the problem? Explain.
- Can you use combinations to solve the problem? Explain.
- Determine the probability. Again, you might find it helpful to create a chart and complete it.
- Suppose three balls have been pocketed, with none of them being the number 9 ball. Determine the probability that all the pocketed balls have a value greater than the number 3 ball.
- Can you use permutations to solve the problem? Explain.
- Can you use combinations to solve the problem? Explain.
- Determine the probability that all the pocketed balls have a value greater than the number 3 ball.
![]() Save your responses in your course folder.
Save your responses in your course folder.
Share 2
With a partner or group, discuss the following based on what you discovered in Try This 3.
- How did you decide when a permutation or a combination was the appropriate method to use in Try This 3?
- Try This 3 question 3 may be determined using a permutation or a combination. Try to solve it again using a different method than you first tried.
1.8. Explore 4
Module 3: Permutations, Combinations, and the Fundamental Counting Principle
In Try This 3, you may have noticed that some problems can be solved using a permutation or a combination; however, most problems will not require you to use both. Generally, problems can be solved using only permutations or by using either combinations or permutations.
This table shows how to solve question 3 from Try This 3 using permutations.
| 5P3 = 60 | Determine the number of favourable outcomes—that is the number of different ways 3 of the balls numbered 4, 5, 6, 7, and 8 can be pocketed if order is considered important. |
| 8P3 = 336 | Determine the number of total outcomes—that is the total number of ways 3 of the balls numbered 1, 2, 3, 4, 5, 6, 7, and 8 can be pocketed if order is considered important. |
| Determine the probability. |
This table shows how to solve question 3 from Try This 3 using combinations.
| 5C3 = 10 | Determine the number of favourable outcomes—that is the number of different ways 3 of the balls numbered 4, 5, 6, 7, and 8 can be pocketed if order is not considered important. |
| 8C3 = 56 | Determine the number of total outcomes—that is the total number of ways 3 of the balls numbered 1, 2, 3, 4, 5, 6, 7, and 8 can be pocketed if order is not considered important. |
| Determine the probability. |
If you would like another example of how to solve probability problems using combinations, watch the video titled “Probability Using Combinations.”
Self-Check 2
- An e-mail contact list contains 21 friends, 18 family members, and 5 co-workers.
![]()
- Complete questions 4, 7, 11, and 13 from pages 159 to 161 of your textbook. Answer
1.9. Connect
Module 3: Permutations, Combinations, and the Fundamental Counting Principle
Complete the Lesson 5 Assignment that you saved in your course folder at the beginning of the lesson. Show work to support your answers.
![]() Save your responses in your course folder.
Save your responses in your course folder.
Project Connection
You are now ready to apply your understanding of permutations and combinations to complete the Module 3 Project. Go to Module 3 Project: Math Mystery, and complete Part 2. Submit the completed project to your teacher for assessment.
1.10. Lesson 5 Summary
Module 3: Permutations, Combinations, and the Fundamental Counting Principle
Lesson 5 Summary
The fundamental counting principle, permutations, and combinations may all be used to solve probability questions depending on the circumstances of the question. It is important to decide whether order is important or not before beginning a question, as this helps to narrow down solution possibilities.
When solving probability questions, you are looking for the likelihood that a particular event occurs. The answer to a probability question is always a number between 0 and 1. A probability of 0 means that the event cannot or does not occur, while a probability of 1 means that the event always occurs. Probability solutions can be written in fraction form, decimal form, or percent form.


