Lesson 2
| Site: | MoodleHUB.ca 🍁 |
| Course: | Math 30-2 SS |
| Book: | Lesson 2 |
| Printed by: | Guest user |
| Date: | Wednesday, 24 December 2025, 8:22 AM |
Description
Created by IMSreader
1. Lesson 2
Module 5: Rational Expressions
Lesson 2: Multiplying and Dividing Rational Expressions
Focus

chistera and ball: Ryan McVay/Photodisc/Thinkstock, Jai Alai game: ©Tilio & Paolo/18284919/Fotolia
What’s your favourite game or sport that is played on a court? Basketball, volleyball, and tennis are some common games played on courts, but have you ever played jai alai?
Jai alai is a sport with Spanish origins played on a large rectangular court called a fronton. The court consists of a floor that can extend up to 200 ft in length and includes three wall surfaces. A player in jai alai bounces a special ball off the front wall using a custom-made basket that is attached to the player’s wrist. A player earns a point if the opponent fails to catch the ball when it rebounds. Known as the fastest sport on Earth and also described as “ballet with bullets,” jai alai can be played one-on-one or with pairs.
In this lesson you will learn how to multiply and divide rational expressions. You will use rational expressions to model the dimensions of the courts in various sports and games, including jai alai.
Lesson Outcomes
At the end of this lesson, you will be able to
- compare the strategies for multiplying and dividing rational expressions to the strategies for multiplying and dividing rational numbers
- determine the non-permissible values when multiplying and dividing rational expressions
- determine, in simplified form, the product or quotient of rational expressions
Lesson Questions
You will investigate the following questions:
- How are multiplying and dividing rational expressions similar to multiplying and dividing rational numbers?
- How are non-permissible values determined when multiplying and dividing rational expressions?
Assessment
Your assessment may be based on a combination of the following tasks:
- completion of the Lesson 2 Assignment (Download the Lesson 2 Assignment and save it in your course folder now.)
- course folder submissions from Try This and Share activities
- work under Project Connection
1.1. Launch
Module 5: Rational Expressions
Launch
Do you have the background knowledge and skills you need to complete this lesson successfully? Launch will help you find out.
Before beginning this lesson, you should be able to
- multiply fractions
- divide fractions
- multiply polynomials
1.2. Are You Ready?
Module 5: Rational Expressions
Are You Ready?
Complete these questions. If you experience difficulty and need help, visit Refresher or contact your teacher.
- How do you multiply fractions? Answer
- Multiply the following fractions. Simplify, where possible.
- How do you divide fractions? Answers
- Divide the following fractions. Simplify, where possible.
- Multiply the following polynomials.
- (2x2)(3x)
- a(a2 − 3b)
If you answered the Are You Ready? questions without problems, move to Discover.
If you found the Are You Ready? questions difficult, complete Refresher.
1.3. Refresher
Module 5: Rational Expressions
Refresher
The interactive multimedia piece Fractions—Multiply and Divide provides a review of how to multiply and divide fractions.
Multiplying Monomials provides a review of how to multiply monomials.
Operations with Polynomials reviews how to multiply a monomial with a binomial.
Go back to the Are You Ready? section and try the questions again. If you are still having difficulty, contact your teacher.
1.4. Discover
Module 5: Rational Expressions
Discover
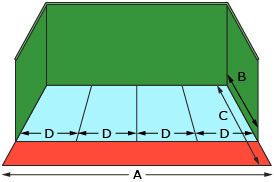
An illustration of a jai alai court is shown. The court consists of three walls shown in green, an in-bounds floor area divided into four sections, and an out-of-bounds area shown in red.
On the court, the dimension B is seven-tenths the length of C. The width of each section, D, is approximately one-quarter the width of the court, A.
(The actual dimensions are ![]() but the estimate
but the estimate ![]() will be used for all of these.)
will be used for all of these.)
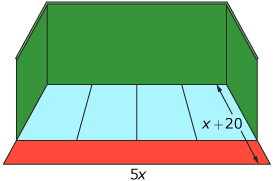
Try This 1
- Write an expression that represents the total court area, including the out-of-bounds area. Remember, area = length × width.
- Write an expression that represents each of the following dimensions of the court:
- length B on the diagram
- length D of the diagram
- the area of one blue section
-
- Write a rational expression that represents the fraction of the total court area occupied by one blue section.
- Simplify this expression.
- If x = 30 ft in the illustration, determine the area of one blue section using the
- expression in 2.c.
- expressions for the dimensions (A and B) of the entire court and applying the original information about the length and width of one blue section
- Compare your results for questions 4.a. and 4.b.
![]() Save your responses in your course folder.
Save your responses in your course folder.
1.5. Explore
Module 5: Rational Expressions
Explore
In the Launch section of this lesson, you reviewed how to multiply rational numbers. In the general case, recall that
Notice that the numerators are multiplied together and that the denominators are multiplied together. The result is then reduced to lowest terms, where possible. In the next activity you will apply this process to multiply rational expressions.
Try This 2
- Explain how the fraction multiplication rule,
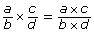 , can be used to determine the product
, can be used to determine the product 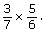
- Explain how the product you determined in question 1 can be simplified.
- Do you think that the fraction multiplication rule in question 1 can be used to multiply the following rational expression? Perform the calculation.
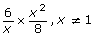
- Use the steps you outlined in question 2 to simplify the product you determined in question 3.
![]() Save your responses in your course folder.
Save your responses in your course folder.
Share 1
Work in a group or with a partner to answer the following questions.
-
- How are the processes of multiplying
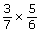 and
and 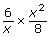 similar?
similar? - How are they different?
- How are the processes of multiplying
-
- How are the processes of simplifying the products similar?
- How are they different?
![]() If required, save a record of your responses in your course folder.
If required, save a record of your responses in your course folder.
1.6. Explore 2
Module 5: Rational Expressions
In Try This 2 you may have noticed that the process for multiplying fractions is similar to multiplying rational expressions.
In question 4 you may have used the principle of prime factorization to help find similar factors to simplify. The multiplication of the rational expression may have looked similar to this:
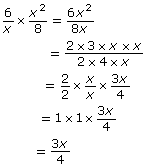
Now explore how non-permissible values are affected by multiplication and simplifying rational expressions.
Try This 3
- Complete the table of values using the rational expressions from Try This 2.
x 
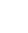
−2 −1 0 1 2 - What do you notice about the values in the table?
- From the table, what are the non-permissible values of the two expressions?
- What do you notice about non-permissible values for equivalent rational expressions?
![]() Save your responses in your course folder.
Save your responses in your course folder.
1.7. Explore 3
Module 5: Rational Expressions
In Try This 3 you saw that non-permissible values may seem to be different for equivalent rational expressions, but that is not the case. As such, non-permissible values must be identified for the original rational expression, and then those same non-permissible values are applied to any other equivalent expression. Restrictions are important to correctly describe what the rational expression represents. Therefore, restrictions must be included with the simplified product. For example, from Try This 3, you would write the following:
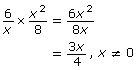
There are two slightly different methods of multiplying and simplifying rational expressions. In the multimedia piece titled Multiplying Rational Expressions, the expressions are first multiplied and then simplified.
In the next example, individual expressions are first simplified and then multiplied together.
Example

Ingram Publishing/Thinkstock
Aki was presented a similar problem, ![]() and had a different idea on how to solve it.
and had a different idea on how to solve it.
First, Aki stated the non-permissible values by looking at the denominators of each fraction.
a ≠ 0
Her next step involved simplifying each individual fraction using prime factorization.
![]()
She then simplified each fraction.
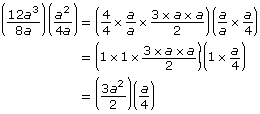
Aki then multiplied the numerators and denominators.
![]()
She then looked for further simplification but noticed there wasn’t any. So her final answer is
![]()
Aki’s solution is just another method of multiplying two rational expressions together.
Self-Check 1
1.8. Explore 4
Module 5: Rational Expressions
Next, you will multiply rational expressions that include binomial numerators or denominators. The same fraction multiplication rule you used in Try This 2 is used when you have rational expressions with binomials.
In the next Try This activity you will multiply rational expressions of various forms. Don’t forget to include the non-permissible values when necessary.
Try This 4
For each question, complete the following:
- Multiply the rational expressions as you would rational numbers.
- Reduce to lowest terms, where possible.
- Include the non-permissible values with your final answer.
![]() Save your responses in your course folder.
Save your responses in your course folder.
Share 2
Compare your answers and strategies from Try This 4 with a partner. Discuss the following questions with your partner.
- Is it necessary to expand an expression such as
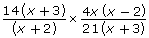 before multiplying? Explain.
before multiplying? Explain. - Why is factoring a useful step in simplifying an expression?
![]() If required, save a record of your discussion in your course folder.
If required, save a record of your discussion in your course folder.
1.9. Explore 5
Module 5: Rational Expressions
Read “Example 1” on page 233 of your textbook. Compare Liam’s steps to the steps you used in Try This 4. Would you change the way you found your solutions in Try This 4 now? Notice at what point Liam used factoring to simplify the problem.
Self-Check 2
Complete questions 6 and 10 on page 239 of your textbook. Answers
Now that you have explored multiplication of rational expressions, you will focus on division. Recall that dividing rational numbers is a process that involves multiplying the first number by the reciprocal of the second number.
How does the division of rational expressions compare with the division of rational numbers? In Try This 5 you will explore both procedures.
Try This 5
- Determine the quotient
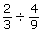 without using your calculator.
without using your calculator. - Describe a procedure for solving
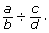 You may want to revisit your answer to question 3 in the Are You Ready? section.
You may want to revisit your answer to question 3 in the Are You Ready? section. - Apply the same procedure described in question 2 to determine the quotient of each of the following expressions.
- How can you check to see if your answers to question 3 are equivalent to the original expression?
![]() Save your work in your course folder.
Save your work in your course folder.
Share 3
Compare your results from Try This 5 with a partner, and discuss the following questions.
In question 3.b., you divided rational expressions that had a common denominator. Consider the expression ![]() What is the result when the expression is simplified? Can you and your partner uncover a pattern to describe a short cut that leads to the same answer?
What is the result when the expression is simplified? Can you and your partner uncover a pattern to describe a short cut that leads to the same answer?
![]() If required, save a record of your discussion in your course folder.
If required, save a record of your discussion in your course folder.
1.10. Explore 6
Module 5: Rational Expressions
Be very careful when inputting the expressions into your calculator. Make sure you put brackets where appropriate to ensure that the calculator performs the correct order of operations. If the two expressions are equal, the graphs will be the same. For some calculators, you can change the thickness of a graph so that you can see more clearly that the two graphs are, in fact, identical.
In Try This 5 you uncovered a pattern for dividing rational expressions; but when you divide rational expressions, the non-permissible values must be identified. In Try This 6 you will explore how non-permissible values are found when dividing rational expressions.
Try This 6
- Complete a table of values like the one shown for the two rational expressions. In the first row, state the non-permissible values determined by looking at the denominators. In the next rows, substitute in the given values of x and calculate the value of the rational expression.
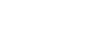
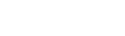
non-permissible values determined by looking at the denominators x = −2 x = −1 x = 0 x = 1 x = 2 x = 3 - What do you notice about the values in the table?
- From the table, what are the non-permissible values of the two expressions?
- When dividing rational expressions, where are the non-permissible values located? Is it sufficient to look at the denominators only?
![]() Save your work in your course folder.
Save your work in your course folder.
1.11. Explore 7
Module 5: Rational Expressions
As you saw in Try This 5, dividing rational expressions is similar to dividing rational numbers. One difference is that, in the case of rational expressions, you must state the non-permissible values. In Try This 6 you may have noticed that non-permissible values will occur when a denominator is equal to 0 if the second expression (the divisor) is equal to 0.
Watch Dividing Rationals Example, and pay attention to how non-permissible values are determined and how the expression is simplified.
Now that you have navigated through the example, try simplifying the following expression. Remember to state the restrictions of the expression.
![]()
The following instructions will guide you through this solution.
Step 1: Factor each expression.
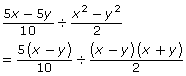
Step 2: State non-permissible values. (Remember to consider both the numerator and denominator of the divisor—the second term of the expression.)
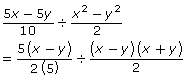
Since the numerator of the divisor will equal 0 if x − y = 0 or x + y = 0, the non-permissible values are x = y and x = − y.
Step 3: Change the division statement into a multiplication statement (i.e., multiply by the reciprocal).
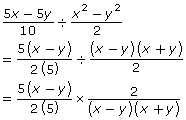
Step 4: Reduce the expression by factoring out any common factors.
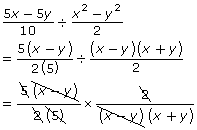
Step 5: Write the simplified expression. Remember to include the non-permissible values.
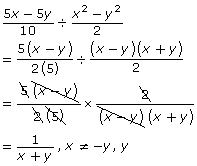
When simplifying rational expressions, you need to apply strategies learned Lessons 1 and 2. Dividing Rational Expressions: Difficult Example shows another example of dividing rational expressions.
Self-Check 3
1.12. Explore 8
Module 5: Rational Expressions
You have now learned how to multiply and divide rational expressions. In the final section of this lesson you will be introduced to the application of rational expressions. This application will be explored more in later lessons.

© Jim/15182266/Fotolia
Self-Check 4
The diagram shows the layout of a lacrosse field. The area outlined in white is called the goal area. The location of the goal is marked by the circle in the goal area.
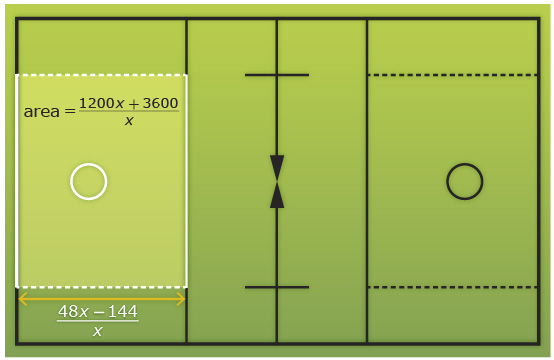
1.13. Connect
Module 5: Rational Expressions
Open the Lesson 2 Assignment you saved in your course folder at the beginning of this lesson. Show work to support your answers.
![]() Save your responses in your course folder.
Save your responses in your course folder.
Project Connection
Go to Module 5 Project: Dice Game Competition. Complete Part 2: Section 1.
Going Beyond
A complex rational expression is a rational expression that contains rational expressions in the numerator and/or denominator. Here is an example:
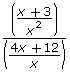
A complex rational expression doesn’t have to be intimidating! You can write the preceding example in the following way:
![]()
You can then factor and simplify as usual. How would you complete this calculation?
![]() Save your response in your course folder.
Save your response in your course folder.
1.14. Lesson 2 Summary
Module 5: Rational Expressions
Lesson 2 Summary
In this lesson you investigated the following questions:
- How are multiplying and dividing rational expressions similar to multiplying and dividing rational numbers?
- How are non-permissible values determined when multiplying and dividing rational expressions?
In this lesson you learned about the similarities between multiplying and dividing rational expressions and multiplying and dividing rational numbers. In both cases, you must multiply numerators with numerators and denominators with denominators. At some point during the process, you must also simplify the result. You discovered that obtaining a simplified result is more easily done when the polynomial expressions in the numerator and denominator are first factored.
One aspect of multiplying and dividing rational expressions that does not emerge in multiplying and dividing rational numbers is the need to determine non-permissible values. You must identify those values of the variable(s) that would result in a 0 denominator as non-permissible.
When dividing rational expressions, you must also consider the numerator of the divisor or the second fraction. Since the numerator becomes the denominator in the course of division, you must also identify as non-permissible the value(s) of the variable(s) that would render the numerator equal to 0.
In the next lesson you will compare the addition and subtraction of rational expressions to the addition and subtraction of rational numbers.