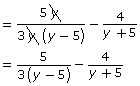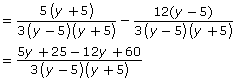Lesson 3
| Site: | MoodleHUB.ca 🍁 |
| Course: | Math 30-2 SS |
| Book: | Lesson 3 |
| Printed by: | Guest user |
| Date: | Wednesday, 24 December 2025, 8:22 AM |
Description
Created by IMSreader
1. Lesson 3
Module 5: Rational Expressions
Lesson 3: Adding and Subtracting Rational Expressions
Focus

Hemera/Thinkstock
In the game of Monopoly, the objective is to acquire and develop real-estate properties in order to build up wealth without going bankrupt. One of the rules of Monopoly is that houses and hotels cannot be constructed on a property unless a player owns all of the properties in the colour group where development is intended. There are different strategies for securing the properties in a particular colour group. For example, the properties can be purchased from the bank or through a real-estate transaction with another player.
In this lesson you will learn how to add and subtract rational expressions. Like the rules for Monopoly, you cannot add or subtract rational expressions until a certain condition is met.
Do you know what this condition is? You will soon. There are different strategies you can employ to meet the condition, including strategies you have previously learned.
Outcomes
At the end of this lesson you will be able to
- compare the strategies for adding and subtracting rational expressions to the strategies for adding and subtracting rational numbers
- determine the non-permissible values when adding and subtracting rational expressions
- determine, in simplified form, the sum or difference of rational expressions with the same denominator, as well as those in which the denominators are not the same and that may or may not contain common factors
- simplify an expression that involves two or more operations on rational expressions
Lesson Questions
You will investigate the following questions:
- How are adding and subtracting rational expressions similar to adding and subtracting rational numbers?
- Can you use the patterns of adding and subtracting rational numbers to determine, in simplified form, the addition or subtraction of rational expressions?
Assessment
Your assessment may be based on a combination of the following tasks:
- completion of the Lesson 3 Assignment (Download the Lesson 3 Assignment and save it in your course folder now.)
- course folder submissions from Try This and Share activities
- work under Project Connection
1.1. Launch
Module 5: Rational Expressions
Launch
Do you have the background knowledge and skills you need to complete this lesson successfully? Launch will help you find out.
Before beginning this lesson, you should be able to
- determine the lowest common multiple of a set of numbers
- add fractions
- subtract fractions
- use order of operations correctly
1.2. Are You Ready?
Module 5: Rational Expressions
Are You Ready?
Complete the following questions. If you experience difficulty or need help, visit Refresher or contact your teacher.
- Determine the LCM (lowest common multiple) of each set of numbers.
- 4 and 6
- 5 and 6
- 10, 12, and 15
Answers - Add or subtract the following rational numbers. Simplify where possible.
Answers - Add or subtract the following rational numbers. Simplify where possible.
Answers - Evaluate the following expressions. Remember that the order of operations is important, so you may want to work each step out on paper.
- 8 × 16 ÷ 4
- 500 − 10 × 15
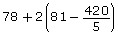
Answers
If you answered the Are You Ready? questions without difficulty, move to Discover.
If you found the Are You Ready? questions difficult, complete Refresher.
1.3. Refresher
Module 5: Rational Expressions
Refresher
Open Least Common Multiple (LCM) to review the definition and to use an applet to find the lowest common multiple of a set of numbers.
Open “Adding Fractions with Unlike Denominators” for a review of addition techniques.
Review subtraction of fractions with “Subtracting Fractions.”
Review how to evaluate expressions using the correct order of operations by watching the videos titled “Order of Operations” and “Order of Operations Example.”
Go back to the Are You Ready? section and try the questions again. If you are still having difficulty, contact your teacher.
1.4. Discover
Module 5: Rational Expressions
Discover
To add and subtract rational numbers, you often have to find the lowest common multiple (LCM) in order to create equivalent fractions that have the same denominators. In this section you will explore two different methods of determining the lowest common multiple for a set of rational expressions.
Try This 1
Method 1: Finding the LCM Using the Factored Form
- Complete a table like the one shown. The first row has been completed to give you an idea of what is expected.
Polynomials
Factored Form
LCM
x2
2x
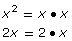
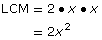
10xy2
4x2y
6x
4x2
x38(a + b)3
4(a2 − b2)
Method 2: Finding the LCM Using Product and GCF
-
- Discover an alternate method of finding the LCM by completing a table like the one shown and then answering the questions that follow. In the table, treat binomials as a single factor. Do not expand (multiply out) any of the factors. The first row has been completed to give you an idea of what is expected.
Expressions
Product
GCF
LCM
GCF • LCM
x2
2x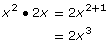
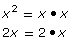
GCF = x
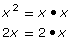
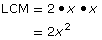
x • 2x2 = 2x3
12xy
15y2(y + 2)
2(y + 2)(x + 3)
(x − 3) - Look at the rows of your completed table. Do you notice any patterns as you look horizontally across the rows? From these patterns, do you see another method you could use to find the LCM?
- Discover an alternate method of finding the LCM by completing a table like the one shown and then answering the questions that follow. In the table, treat binomials as a single factor. Do not expand (multiply out) any of the factors. The first row has been completed to give you an idea of what is expected.
- What other previous math concepts have you learned that required you to work with lowest common multiples?
- Why do you think it is important to be able to have different strategies to determine the LCM of a set of expressions?
![]() Save your responses in your course folder.
Save your responses in your course folder.
1.5. Explore
Module 5: Rational Expressions
Explore

iStockphoto/Thinkstock
Have you ever played backgammon? Backgammon is a classic board game for two players consisting of a special board, dice, and pieces commonly called “checkers” or “stones.” The object of the game is to be the first player to move all of the checkers from their starting position on the board, around a track, and then off the board.
Before a player can begin clearing checkers off the board, the player must move all of the checkers to his or her home base, which is a quadrant of the backgammon board. In the photo the home base for the player in the bottom of the picture is the quadrant directly underneath that player’s outstretched arm. The home base for the player at the top of the picture is the quadrant directly below that player’s left hand. The majority of the game is spent moving checkers to the home base. The first player to move all of his or her checkers to the home base wins the game.
In this lesson you will determine the sums and differences of rational expressions. Just like in backgammon, you will discover that the actual adding and subtracting of expressions is easy—it’s the preparation of the expressions and meeting of certain conditions that can be a time challenge.
1.6. Explore 2
Module 5: Rational Expressions
In the Are You Ready? section, you added and subtracted rational numbers. The question remains: can you verbalize the steps involved in the calculation?
Try This 2
Following are the worked-out steps for ![]() Use the words numerator, denominator, and rational numbers to describe the steps being followed.
Use the words numerator, denominator, and rational numbers to describe the steps being followed.
Question/Steps |
Explanation of Step |
|
|
|
|
|
|
|
|
![]() Save your responses in your course folder.
Save your responses in your course folder.
Share 1
- With a partner, trade your explanations from Try This 2. Use the steps provided by your partner to solve the question
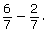
- Do any of the steps need rewording for full understanding?
![]() If required, save a record of your discussion in your course folder.
If required, save a record of your discussion in your course folder.
1.7. Explore 3
Module 5: Rational Expressions
The same method can be applied to the addition and subtraction of rational expressions. As usual with rational expressions, non-permissible values must be considered. When adding and subtracting fractions, you can follow these steps:
- Ensure the two fractions have a common denominator.
- Add or subtract the numerator to find the resulting numerator. The resulting denominator is the same as the common denominator.
- If possible, simplify the fraction by dividing both the numerator and denominator by a common factor.
Try This 3
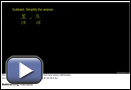
- Simplify the following rational expression using the steps you discussed in Try This 2.
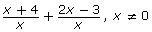
- Do you think you completed question 1 correctly? Verify the sum by graphing the original expression
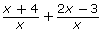 into Y1 = and your result into Y2 = on a graphing calculator. Go to the table and compare the values of Y1 and Y2 for each value of X. For the original expression and the result to be equivalent, the values of Y1 and Y2 must be the same. Ignore values of X that are non-permissible values. Note: As a refresher, you may wish to review question 4 of Try This 5 in Lesson 2.
into Y1 = and your result into Y2 = on a graphing calculator. Go to the table and compare the values of Y1 and Y2 for each value of X. For the original expression and the result to be equivalent, the values of Y1 and Y2 must be the same. Ignore values of X that are non-permissible values. Note: As a refresher, you may wish to review question 4 of Try This 5 in Lesson 2. - Do you think the same procedure would work for a binomial in the denominator? Find out by evaluating the following rational expression.
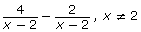
- Do you think you evaluated the expression correctly? Again, verify your results.
![]() Save your responses in your course folder.
Save your responses in your course folder.
Share 2
With a partner, discuss any differences in your responses to Try This 3. Make any necessary revisions once a consensus has been reached.
- Describe a procedure that can be followed to determine the sum or difference, in simplest form, of rational expressions with the same denominator.
- Refer to the graphing method of verifying your answers.
- What do you have to watch out for when using this method?
- Describe a different method you could use to verify your answers.
- After verification, did you or your partner need to revise your calculations? Were you able to find your error(s)?
![]() If required, save a record of your discussion in your course folder.
If required, save a record of your discussion in your course folder.
1.8. Explore 4
Module 5: Rational Expressions
In Try This 3 you may have seen that adding and subtracting rational expressions with common denominators is very similar to adding and subtracting rational numbers. Compare what you did in Try This 3 with the example of adding rational numbers with the following common denominators. How does your method compare?
State the non-permissible values of the rational expression by looking at the denominators. |
|
|||||||
Write the two rational expressions as one expression with the common denominator x − 3. |
|
|||||||
Simplify the numerator, and state the |
|
|||||||
Verify your answer. |
|
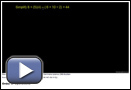
The following example shows how to prevent a common error that occurs when evaluating rational expressions in subtraction. Pay attention to how parentheses are used to keep the binomials in the numerator separated to start and how this expression is then simplified.
Example
![]()

Verification
Plot 1 Plot 2 Plot 3 |
X |
Y1 |
Y2 |
−3 |
−.3333 |
−.3333 |
Consider another example. Notice that, before simplifying, the denominator of the sum is the same as the denominator of the original rational expressions. Also pay attention to how factoring is used to simplify the expression.
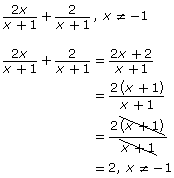
Why is there still a restriction placed on the solution? ![]()
Why were no parentheses shown in the second line of this solution? When are they necessary? ![]()
Self-Check 1
1.9. Explore 5
Module 5: Rational Expressions
You have discovered that adding or subtracting rational expressions is relatively straightforward when the expressions have common denominators. What do you do when the denominators are different?
Before moving to Try This 4, make sure you understand how to determine the lowest common multiple of two numbers. If you feel you need a review of the two methods, watch Making Equivalent Fractions: Factored Form and Making Equivalent Fractions: GCF × LCM to see these methods in action.
Try This 4
In the Are You Ready? section, you added and subtracted rational numbers that had different denominators. Still, the question remains: can you verbalize the steps involved in the calculation?
Following are the worked-out steps for ![]() Use the words numerator, denominator, and rational numbers to describe the steps being followed.
Use the words numerator, denominator, and rational numbers to describe the steps being followed.
Question/Steps |
Explanation of Step |
|
|
12 = 2 × 2 × 3
|
|
|
|
|
|
|
|
|
|
|
|
![]() Save your responses in your course folder.
Save your responses in your course folder.
Share 3
- Switch explanations with a partner. Use the steps provided by your partner to solve the question
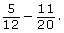
- Do any of the steps need rewording for full understanding?
![]() If required, save a record of your discussion in your course folder.
If required, save a record of your discussion in your course folder.
1.10. Explore 6
Module 5: Rational Expressions
In Discover, two different ways to determine the lowest common multiple (LCM) for any group of denominators were explored. Retrieve your results and review the two methods—the factored form method and the product and GCF method.
Once you have a full understanding of finding the lowest common denominators (LCD) with rational expressions, complete Try This 5. Remember, the same method can be applied to the addition and subtraction of rational expressions with different denominators. As usual with rational expressions, non-permissible values must be considered.
Try This 5
- Simplify the following rational expression using the steps you discussed in Try This 4.
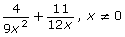
- Verify your results.
![]() Save your responses in your course folder.
Save your responses in your course folder.
Share 4
With a partner, discuss any differences in your responses to Try This 5. Make any necessary revisions once a consensus has been reached. This will give both of you a better understanding of the process required.
- Describe a procedure that can be followed to determine the sum or difference, in simplest form, of rational expressions with different monomial denominators.
- Refer to the graphing method of verifying your answers.
- What do you have to watch out for when using this method?
- Describe a different method you could use to verify your answers.
- After verification, did you or your partner need to revise your calculations? Were you able to find your error(s)?
![]() If required, save a record of your discussion in your course folder.
If required, save a record of your discussion in your course folder.
1.11. Explore 7
Module 5: Rational Expressions
You saw in Try This 5 that when adding rational expressions with different denominators, you need to first find a common denominator. Adding Fractions illustrates this process.
Consider the following example:
![]()
The first step is always to state the non-permissible value. Looking at the denominators, you can see that a ≠ 0.
Next, find the lowest common denominator. Find the prime factorization of each denominator.
15a = 3 × 5 × a
5a2 = 5 × a × a
Therefore, the LCD is 3 × 5 × a × a = 15a2.
Multiply each expression by a fraction that is equal to 1, so each expression has the denominator 15a2.
![]()
Now each denominator is the same. Simplify.
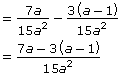
Subtract the numerators.
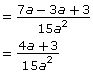
Make sure to include the restrictions from the original expressions.
![]()
Self-Check 2
Complete questions 1.a., 1.b., and 4 on page 249 of the textbook. Answers
1.12. Explore 8
Module 5: Rational Expressions
The factors of the denominator of a rational expression can be a
- constant
- monomial
- binomial
In any of these cases, consider factoring the denominator to its simplest form to help determine the lowest common denominator.
Try This 6
- Do you think the strategy you have used to add and subtract rational expressions so far will work for rational expressions that have binomials in the denominator? Find out by simplifying the following rational expression.
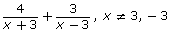
- Did you need to factor before finding the LCD?
- Did you add the expressions correctly? Verify your results.
- Now try simplifying this rational expression.
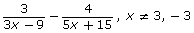
- Did you need to factor before finding the LCD?
- Did you subtract the expressions correctly? Verify your results.
![]() Save your responses in your course folder.
Save your responses in your course folder.
Share 5
With a partner, discuss any differences in your responses to Try This 6. Make any necessary revisions once you both agree on the clearest explanation of the process required.
- Describe a procedure that can be followed to determine the sum or difference, in simplest form, of rational expressions with different binomial denominators.
- After verification, did you or your partner need to revise your calculations? Were you able to find your error(s)?
![]() If required, save a record of your discussion in your course folder.
If required, save a record of your discussion in your course folder.
1.13. Explore 9
Module 5: Rational Expressions
In Try This 6 you learned that there are times when you need to factor the rational expression before determining the LCD. Look at another example.
Simplify. |
|
The first step is to always state the non-permissible value.
You will need to factor in order to find the values of y that will restrict the expression.
Therefore, the restrictions are y ≠ 0, 5, −5. |
|
Next, find the LCD.
Simplify the first expression by cancelling the 1 of
The LCD equals 3(y − 5)(y + 5). |
|
Multiply each expression by a fraction that is equal to 1 so each ends up with the denominator 3(y − 5)(y + 5). |
|
Now each denominator is the same. Simplify. |
|
Subtract the numerators. |
|
Make sure to include the restrictions from the original expressions. |
|
To see another example of factoring, read “Example 4” on pages 247 and 248 of your textbook. Notice when factoring is used to help add the rational expressions.
Try This 7
Complete Adding Rationals. This example is similar to “Example 4” that you just read in the textbook. After you complete the multimedia piece, answer the questions that follow.
- Why was the denominator of the first rational expression factored before a common denominator was determined?
- Why was it necessary to factor the numerator when trying to simplify
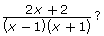
- Why is −1 included as a non-permissible value for the final expression
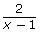 when −1 does not make the denominator zero?
when −1 does not make the denominator zero?
![]() Save your work in your course folder.
Save your work in your course folder.
Self-Check 3
![]()
- Complete questions 1.d., 5.a., 5.b., 7, 8, and 9 on pages 249 and 250 of the textbook. Answers
1.14. Connect
Module 5: Rational Expressions
Complete the Lesson 3 Assignment that you saved in your course folder at the beginning of the lesson. Show work to support your answers.
![]() Save your responses in your course folder.
Save your responses in your course folder.
Project Connection
Go to Module 5 Project: Dice Game Competition. Complete Part 2: Section 2.
Going Beyond
In this lesson you looked at rational expressions with monomial or binomial denominators. Denominators can be any polynomial. Consider the following example of subtracting two rational expressions with trinomial denominators:
![]()
How would you solve this subtraction problem?
1.15. Lesson 3 Summary
Module 5: Rational Expressions
Lesson 3 Summary
In this lesson you investigated the following questions:
- How are adding and subtracting rational expressions similar to adding and subtracting rational numbers?
- Can you use the patterns of adding and subtracting rational numbers to determine, in simplified form, the addition or subtraction of rational expressions?
You discovered that adding and subtracting rational expressions is similar to adding and subtracting rational numbers. In both cases, you must do the following:

iStockphoto/Thinkstock
Step 1: State any non-permissible values.
Step 2: Determine the lowest common denominator (LCD).
Step 3: Use the property of 1 to write equivalent rational expressions over the LCD.
Step 4: Add or subtract the numerators, and then simplify.
You discovered that the order of steps for these procedures is important. You learned two strategies for determining the lowest common denominator. One method is based on a strategy similar to prime factorization. The other method is based on the pattern that the lowest common denominator is equal to the product of the denominators divided by the greatest common factor:
![]()
In the next lesson you will continue to see how useful the lowest common denominator is when solving rational equations.