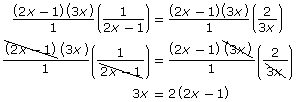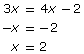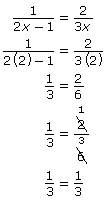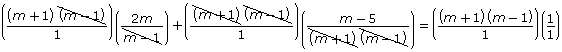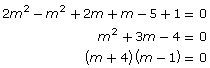Lesson 4
| Site: | MoodleHUB.ca 🍁 |
| Course: | Math 30-2 SS |
| Book: | Lesson 4 |
| Printed by: | Guest user |
| Date: | Wednesday, 24 December 2025, 8:22 AM |
Description
Created by IMSreader
1. Lesson 4
Module 5: Rational Expressions
Lesson 4: Solving Rational Equations
Focus

Jupiterimages/Goodshoot/Thinkstock
Many reality television shows are based on competition between individuals or teams of people. Contestants compete in challenges for the right to remain in the game. Challenges may involve navigating an obstacle course, solving a puzzle, finding a hidden object, or any combination of these or other tasks.
In a way, solving equations in mathematics is similar to these tasks. When solving equations, you often have to navigate through several steps in order to find the unknown variable or the “hidden object.”
In this lesson you will learn to solve rational equations. You will learn basic principles that will help you tackle a wide variety of problems.
Outcomes
At the end of this lesson, you will be able to
- determine the non-permissible values for the variable in a rational equation
- determine the solution to a rational equation algebraically and explain the process used to solve the equation
- explain why a value obtained in solving a rational equation may not be a solution of the equation
Lesson Questions
In this lesson you will investigate the following questions:
- What are the different strategies used, and how are they helpful in solving rational equations?
- Why are some values of the variable obtained in solving rational equations not roots of the equations?
Assessment
Your assessment may be based on a combination of the following tasks:
- completion of the Lesson 4 Assignment (Download the Lesson 4 Assignment and save it in your course folder now.)
- course folder submissions from Try This and Share activities
- additions to Glossary Terms
- work under Project Connection
1.1. Launch
Module 5: Rational Expressions
Launch
Do you have the background knowledge and skills you need to complete this lesson successfully? Launch will help you find out.
Before beginning this lesson, you should be able to solve linear and quadratic equations.
1.2. Are You Ready?
Module 5: Rational Expressions
Are You Ready?
Complete the following questions. If you experience difficulty and need help, visit Refresher or contact your teacher.
- Solve the following equations.
- 2(x + 1) = (1 − x) + x + 3
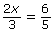
Answers - Solve the following quadratic equations by factoring.
- 2x2 = 7x − 6
- (p + 5)(p − 2) = 2(p − 4)
Answers - Solve the following quadratic equations using the quadratic formula.
- x2 − 2x = 4
- 3x(x − 4) = 2(5 − x2)
Answers
If you answered the Are You Ready? questions without difficulty, move to Discover.
If you found the Are You Ready? questions difficult, complete the Refresher.
1.3. Refresher
Module 5: Rational Expressions
Refresher
To review how to solve linear equations, watch “Algebra: Linear Equations 4.”
Watch the video titled “Solving Quadratic Equations by Factoring” to review a solution to a quadratic equation.
Watch “Quadratic Formula 1” to review solving quadratic equations using the quadratic formula.
Go back to the Are You Ready? section and try the questions again. If you are still having difficulty, contact your teacher.
1.4. Discover
Module 5: Rational Expressions
Discover
Try This 1
Following are three equations that appear very different. But are they really? Complete the questions in order to find out.
Equation A |
Equation B |
Equation C |
|
0.125x + 0.25x = 6 |
3x + 6x = 144 |
- Solve each of the equations. Begin with the equation you think would be the easiest to solve. Show all of your work.
- What do you notice about the root or solution of each equation?
- What is the relationship between the three equations?
- Explain how you can convert between each of the following equations:
- equation A to equation C
- equation A to equation B
![]() Save your responses in your course folder.
Save your responses in your course folder.
1.5. Explore
Module 5: Rational Expressions
Explore

iStockphoto/Thinkstock
What strategies do you use when tackling difficult jigsaw puzzles? Do you begin by assembling the border? Do you collect certain pieces that have the same colour or that may be used to create distinct parts of the puzzle? These strategies and others can help to reduce a pile of random puzzle pieces into a beautiful picture.
In this lesson you will learn how to solve rational equations. Like your approach to a puzzle, you can use strategies to make unravelling the final picture—the solution—much easier.
A rational equation is an equation that contains rational expressions.
Examples of Rational Equations |
||
|
|
|
To solve a rational equation, you must isolate the unknown variable, just as you would to solve any other equation. Since you need to eliminate the denominators, there is an extra step in solving rational equations.
Retrieve your work from Discover. In Try This 1 you discovered that each of the three equations had the same root. This is because the three equations are equivalent. In other words, you can determine the answer to equation A by solving equation B or equation C.
Equation B and equation C were easier to solve because they did not contain rational expressions. Generally speaking, an equation is easier to solve when you don’t have to work with denominators.
In Discover you explored personal strategies for converting between different equation types. In this lesson you will mostly use the lowest common denominator to clear the denominators.
Try This 2
Consider the following rational equation:
![]()
- Determine the non-permissible value(s).
- Determine the lowest common denominator.
- Multiply the expression on each side of the equation by the LCD.
- Solve the resulting equation for x.

![]() Save your responses in your course folder.
Save your responses in your course folder.
Share 1
Compare your answers to Try This 2 with a partner. Discuss any discrepancies in the solution process and in the result. Come to an agreement on how to resolve any discrepancies. Then discuss the following questions based on Try This 2.
- What was the purpose of the step in question 3?
- Do you have to use the LCD to determine the correct answer? Give reasons to support your answer.
- Why is it important to determine the non-permissible value(s) at the beginning of the solution process instead of waiting until the end?
- In this case, the non-permissible value is different from the final answer. What if you ended up with a final answer that was equal to a non-permissible value? Do you think that is possible?
- What is one method you could use to verify your solution?
![]() If required, save your responses in your course folder.
If required, save your responses in your course folder.
1.6. Explore 2
Module 5: Rational Expressions
If you had difficulty solving Try This 2, watch Steps for Solving Rational Equations for a visual of the solution.
Compare the steps you used to solve the rational equation to the steps used to solve the rational equation in the next Try This.
Try This 3
Work through Solving a Rational Equation to help you understand the steps involved in solving rational equations. Then answer the questions that follow.
- How do you multiply the LCD against each side of the equation?
- Why do you end up with a quadratic equation after multiplying each side of the equation by the LCD? Will this happen every time?
![]() Save your responses in your course folder.
Save your responses in your course folder.
1.7. Explore 3
Module 5: Rational Expressions
Try This 2 and Try This 3 focused on the steps involved in solving rational equations.
Step 1: Determine any non-permissible values.
Step 2: Multiply both sides of the equation by the LCD.
Step 3: Eliminate common factors.
Step 4: Solve the simplified equation.
Step 5: Check if the solutions are extraneous.
To confirm that you understand the process of solving simple rational equations, review the solution for ![]()
Step |
Your Work |
Step 1: Determine the non-permissible values. |
|
Step 2: Determine the LCD. |
LCD = (2x − 1)(3x) |
Step 3: Multiply by the LCD. |
|
Step 4: Simplify and solve the linear equation. |
|
Step 5: Check your solutions to see if they are extraneous.
Step 1 indicates that 2 is not a non‑permissible value.
Verify the solution by substituting 2 into the original equation and solving for each side. |
Since the LS = RS, the solution x = 2 is correct. |
Self-Check 1
Complete Solving Rational Equations Self-Check.
1.8. Explore 4
Module 5: Rational Expressions
You have now learned the basics of solving rational equations. You can apply the principles you have learned to other rational equations. In order to identify the lowest common denominator more easily, try factoring the denominators. Keep this in mind as you complete Try This 4.
Try This 4
Study the following rational equation:
![]()
How would you solve this equation? The approach you learned previously can be applied here. Create a table like the following, and complete the steps to determine the solution.
Step |
Your Work |
Step 1: Determine the non-permissible values. |
|
Step 2: Determine the LCD. |
|
Step 3: Multiply by the LCD. |
|
Step 4: Solve for x. |
|
Step 5: Check your solutions to see if they are extraneous. |
|
![]() Save your work in your course folder.
Save your work in your course folder.
Share 2
With a partner, discuss the following questions.
- Compare and contrast the work required to solve
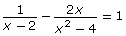 to the work that was required to solve
to the work that was required to solve 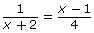 in Try This 2.
in Try This 2. - In the last step, you should have obtained two possible roots. However, did you notice that one of the roots is also a non-permissible value? What does this imply?
![]() If required, save your responses in your course folder.
If required, save your responses in your course folder.
1.9. Explore 5
Module 5: Rational Expressions
The steps you used in Try This 4 may have been similar to the steps shown in the following example. After reviewing the example, think about any changes you might want to make to your solution in Try This 4.
Solve ![]()
Factor. |
|
Determine the non‑permissible values. |
m ≠ ±1 |
Find the LCD. |
LCD = (m − 1)(m + 1) |
Multiply each term on both sides of the equation by the LCD, and cancel common factors. |
|
Multiply the remaining rational expressions. |
|
Since this is a quadratic equation, manipulate the equation by bringing all terms to one side and solve by factoring. |
|
The solutions are m = −4 or m = 1. Check to see if the solutions are extraneous. Since one of the non-permissible values is 1, m = 1 is extraneous. |
Therefore, the only solution is m = −4. |
If you feel you need additional help, review “Example 2” on page 254 of your textbook. In this example, Marlene solves the equation, but the answer is a non-permissible value, which means there is no solution. The example should remind you to be aware of solutions that can’t be used since they are non-permissible. These solutions are called extraneous roots.
Self-Check 2
Complete questions 4, 5, and 6 on page 258 of your textbook. Answers
Add the following terms to your copy of Glossary Terms:
- rational equation
- extraneous root
1.10. Connect
Module 5: Rational Expressions
Complete the Lesson 4 Assignment that you saved in your course folder at the beginning of the lesson. Show work to support your answers.
![]() Save your responses in your course folder.
Save your responses in your course folder.
Project Connection
Go to Module 5 Project: Dice Game Competition. Go to Part 3: Section 1 and complete an application type of question.
Going Beyond

iStockphoto/Thinkstock
The following is a common physics problem.
A railway car is moving east at 6.25 m/s and collides with another stationary car with a mass of 9.64 x 104 kg. The two freight cars join together at impact and the resulting velocity is 2.89 m/s. What is the mass of the railway car that was originally in motion?
Use the formula ![]() where
where
V is the combined velocity of both objects after collision
m is the mass of the object in motion
v is the velocity of the object in motion
M is the mass of the stationery object
Since you need to solve for m, manipulate the formula. You use similar strategies of solving rational equations to help manipulate the formula for another variable.
Manipulate the formula so you isolate m.
1.11. Lesson 4 Summary
Module 5: Rational Expressions
Lesson 4 Summary

Jupiterimages/Polka Dot/Thinkstock
In this lesson you investigated the following questions:
- What are the different strategies used, and how are they helpful in solving rational equations?
- Why are some values of the variable that are obtained in solving rational equations not roots of the equations?
You discovered that solving rational equations is like solving puzzles. The approach taken should simplify the overall task. In the case of rational equations, clearing the denominators is a good way to simplify the task. By doing so, you are left with either a linear or a quadratic equation to solve. Solving for the unknown in a rational equation is not the last step. Extraneous roots occur when the value of the variable obtained is also a non-permissible value. Non-permissible values are unique to rational expressions where a variable occurs in the denominator. However, since the solution process involves solving an equivalent non-rational equation (with no denominators; hence, no restrictions), it is possible for an extraneous solution to be obtained.
In the next lesson you will learn how to model problems with rational equations. You will use the strategies you developed in this lesson to solve those problems.