Lesson 5
| Site: | MoodleHUB.ca 🍁 |
| Course: | Math 30-2 SS |
| Book: | Lesson 5 |
| Printed by: | Guest user |
| Date: | Wednesday, 24 December 2025, 8:27 AM |
Description
Created by IMSreader
1. Lesson 5
Module 5: Rational Expressions
Lesson 5: Applications of Rational Equations
Focus

iStockphoto/Thinkstock
It’s Super Challenge Day! Two-person teams will compete to win three different challenges and the right to be crowned Super Challenge Champions. Teams compete in events such as Scooter Rendezvous, Flyer Scramble, and Mixture Madness.
In the previous lesson you learned how to solve rational equations. In this lesson you will use the strategies learned to solve practical problems involving rational equations that will centre on the events of Super Challenge Day.
Lesson Outcome
At the end of this lesson you will be able to solve contextual problems by using a rational equation.
Lesson Question
You will investigate the following question: How can real-world problems be modelled with rational expressions and rational equations?
Assessment
Your assessment may be based on a combination of the following tasks:
- completion of the Lesson 5 Assignment (Download the Lesson 5 Assignment and save it in your course folder now.)
- course folder submissions from Try This and Share activities
- work under Project Connection
1.1. Launch
Module 5: Rational Expressions
Launch
Do you have the background knowledge and skills you need to complete this lesson successfully? Launch will help you find out.
Before beginning this lesson, you should be able to
- evaluate distance, speed, and time problems
- solve rational equations
1.2. Are You Ready?
Module 5: Rational Expressions
Are You Ready?
Complete the following question. If you experience difficulty and need help, visit Refresher or contact your teacher.
The distance (d) that has been travelled at speed (v) over time (t) is given by d = vt. Use this formula to evaluate the
- distance travelled by a car with speed 90 km/h after 2.5 h Answer
- speed of a motorcycle if it travels 500 km in 4 h Answer
- time it takes for a man to walk 12 km at a speed of 5 km/h Answer
If you answered the Are You Ready? questions without difficulty, move to Discover.
If you found the Are You Ready? questions difficult, complete Refresher.
1.3. Refresher
Module 5: Rational Expressions
Refresher
Practise calculating distance, speed, and time problems by completing Uniform Motion: Calculating Speed, Distance, and Time.
Go back to the Are You Ready? section and try the questions again. If you are still having difficulty, contact your teacher.
1.4. Discover
Module 5: Rational Expressions
Discover

iStockphoto/Thinkstock
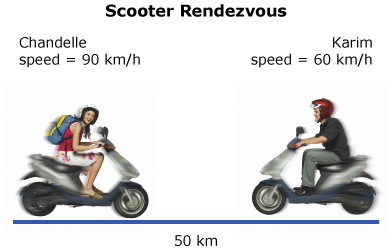
The first event at Super Challenge Day is Scooter Rendezvous. Scooters have long represented a fun and economical way of travelling. Not all scooters are built the same. Some scooters have larger engines, others have more storage room, and all have unique designs.
In Scooter Rendezvous, team members start at opposite ends of a 50-km stretch of highway. Each team member drives toward the other. The event is completed when the scooters meet. The time it takes each team to complete the event is recorded, and winners are declared based on the fastest times.
Try This 1
Karim and Chandelle participated in Scooter Rendezvous. Karim drove his scooter at an average speed of 60 km/h. Chandelle drove her scooter at an average speed of 90 km/h.
scooters: George Doyle/Stockbyte/Thinkstock
- Use the diagram to help you place the information from the question into a chart like the following. Where a quantity is unknown, use a variable or expression.
Distance (km)
Speed (km/h)
Karim
Chandelle

- If Karim and Chandelle start the race at the exact same time, what do you know about the time it took each of them to arrive at the rendezvous point?
- Choose a strategy that you could use to determine the distance travelled by each driver. Ask yourself these questions if you get stuck:
- What is an algebraic strategy I could use?

- What is a second strategy that I can use?

- What is an algebraic strategy I could use?
![]() Save your work in your course folder. You will revisit these results later in the lesson.
Save your work in your course folder. You will revisit these results later in the lesson.
1.5. Explore
Module 5: Rational Expressions
Explore
Consider the following types of problems:
- If you could shovel your driveway in 30 min and your friend could do the same job in 25 min, how long would it take both of you to do the job together?
- How much time do you actually save on a 60-km drive if you drive 15 km/h over the speed limit?
- What amount of floor cleaner do you have to add to a bucket containing 10 L of water to create a solution that is 5% floor cleaner?

left to right: Hemera/Thinkstock, Steve Mason/Photodisc/Thinkstock, Thinkstock Images/Comstock/Thinkstock
These types of problems can be solved using rational equations. In fact, rational equations can be used to model and solve many problems related to work, motion, and proportions.
Problem solving is perceived as being difficult by some students. Here are some strategies to help with application-type questions:
- Strategy 1: Look for key words in the problem.
- Strategy 2: Make a table or an organized list.
- Strategy 3: Draw a picture or a graph.
- Strategy 4: Look for patterns.
- Strategy 5: Work backwards.
- Strategy 6: Guess and check.

iStockphoto/Thinkstock
Using the six strategies, you will focus on three particular types of applications that involve rational equations: work problems, motion problems, and proportion problems.
Solving a word problem can be challenging, but doing so does not have to be difficult. Careful reading, proper planning, and a good understanding of mathematics are keys to success in modelling and solving word problems.
In Discover, you had to determine the distance travelled by each scooter. You organized your information in a table. It should look similar to the table shown.
|
Distance (km) |
Speed (km/h) |
Karim |
d |
60 |
Chandelle |
50 − d |
90 |
You can use the organized information to determine an expression for the time taken by each person to complete his or her portion of the event.
Recall that time is equal to the ratio of the distance travelled divided by the speed, or ![]() The expressions for the time taken by Karim and Chandelle to complete the event are shown in the table.
The expressions for the time taken by Karim and Chandelle to complete the event are shown in the table.
|
Distance (km) |
Speed (km/h) |
Time |
Karim |
d |
60 |
|
Chandelle |
50 − d |
90 |
|
Since Karim and Chandelle start and stop driving at the same time (i.e., when the scooters meet), their time travelled should be identical. In other words, Karim’s time = Chandelle’s time.
Substitute the expressions that represent time from the table above to get the following rational equation.
![]()
Try This 2
- Solve the equation
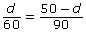 for d. How far did Karim travel? How far did Chandelle travel?
for d. How far did Karim travel? How far did Chandelle travel? - Compare your answers to those you determined in Try This 1 question 3. Are your answers the same?
- How much time did it take for Karim and Chandelle to complete the event?
![]() Save your responses in your course folder.
Save your responses in your course folder.
Share 1
Work with a partner or a group to complete the following questions.
- How can you check to see if your answers are correct?
- Did you check for extraneous solutions?
![]() If required, save a record of your discussion in your course folder.
If required, save a record of your discussion in your course folder.
1.6. Explore 2
Module 5: Rational Expressions
In Try This 2, you may have found that Karim travelled 20 km and Chandelle travelled 30 km. They both took 20 min to complete the event since they started and ended at the same time.
Self-Check 1
1.7. Explore 3
Module 5: Rational Expressions

Hemera/Thinkstock
Another event at Super Challenge Day is the Flyer Scramble. Flyers are a great way to let people know about community events, new businesses, and missing pets.
In this event, teams of two must deliver flyers to 100 homes. Flyers must be placed inside mailboxes, and team members must only use walkways. Each team member completes the challenge and is timed. The results are used to calculate the time it would take to complete the route by both team members working simultaneously.
Each team member then runs through the route to attempt to beat the calculated time. The winning team is the team with the fastest actual recorded or calculated time.
Try This 3
Mitchell and Tia are members of a team participating in the Flyer Scramble event. Mitchell can deliver the flyers in 40 min. Tia covers the same route in 50 min. Open up the Flyer Scrambler applet that shows the routes being completed separately and then together.
Now that you have played with the applet, answer the following questions based on your observations.
- Determine the fraction of the flyers Mitchell could deliver in
- 10 min
- 20 min
- 40 min
- What fraction of the flyers could Mitchell deliver in t min? How did you determine this?
- Determine the fraction of the flyers Tia could deliver in
- 10 min
- 20 min
- 50 min
- What fraction of the flyers could Tia deliver in t min? How did you determine this?
- What does the fraction
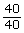 mean for Mitchell?
mean for Mitchell?
- The applet shows that it takes Mitchell and Tia approximately 22.2 min to complete the route together. The rational equation that represents the time it takes both Mitchell and Tia to complete the route is
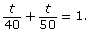
- What does the expression
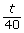 represent?
represent? - What does the expression
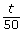 represent?
represent? - When you add the two fractions together, why do they equal 1?

- Verify that the time it would take Tia and Mitchell working together is 22.2 min.
- What does the expression
Share 2
Work with a partner to complete the following questions.
- The average time between Tia and Mitchell is 45 min. Why would this not be the answer to the problem?
- What if Mitchell did the route in 38 min (which is 2 min quicker than he is doing it now) and Tia did it in 52 min (which is 2 min slower than she is doing it now)? Would they still do the route together in 22.2 min? Explain your estimation.
![]() If required, save a record of your discussion in your course folder.
If required, save a record of your discussion in your course folder.
1.8. Explore 4
Module 5: Rational Expressions
In Try This 3, you may have discovered that Tia and Mitchell completed the flyer route in 22.2 min by working together.
For a similar example, read “Example 3” on page 255 of your textbook. Pay attention to the expressions that illustrate the fraction of flyers delivered in 1 min and the solution to the equation if Stuart and Lucy were to work together to deliver flyers.
Self-Check 2
Complete questions 10, 12, and 14 on page 259 of your textbook. Answers
1.9. Explore 5
Module 5: Rational Expressions

iStockphoto/Thinkstock
The third event at Super Challenge Day is Mixture Madness. Mixing items of two different concentrations can help create the perfect blend to suit your needs, whether you need motor oil and gasoline, trail mix, or ketchup and mustard.
In Mixture Madness, team members combine ingredients to prepare mixtures containing a predetermined proportion of a specified ingredient. Contestants use tools to measure the mass and the volume of the ingredients. Points are deducted according to the discrepancy between the obtained measure and the target measure. The winning team is the team with the fewest deductions.
Try This 4
Can you determine the rational equation that is used to compute the percentage concentration of the solution given a specific volume of water?
Launch the Bleach Solution applet to experiment with different mixtures of concentrated bleach and water. Move the bleach slider to input a volume of bleach that is less than 10 L. Use the water slider to input a volume of water that is less than 100 L. Incremental changes can be made to both sliders using the arrow keys on your keyboard after the sliders are selected. The percentage solution that is created is shown above the container.
Now that you have experimented with the applet, hopefully you have concluded that changing the volume of bleach and/or water changes the percentage concentration of the solution. But can you determine the percentage concentration mathematically?
Consider the following: How much bleach should be added to 50 L of water in order to make a solution that is 10% bleach?
- Remember that percentage concentration is given by
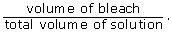 Complete a chart similar to the following to help you observe the patterns involved.
Complete a chart similar to the following to help you observe the patterns involved.
Volume of Bleach (L)
Volume of Water (L)
Percentage Concentration of Bleach
5 L
50 L
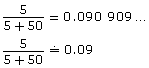
10 L
50 L
15 L
50 L
20 L
50 L
x
50 L
- Using your completed table, write a rational equation that can be used to solve the original problem: How much bleach should be added to 50 L of water in order to make a solution that is 10% bleach? For additional help, use the hints provided.


- Solve the equation. Use the Bleach Solution applet to confirm your answer.
![]() Save your work in your course folder.
Save your work in your course folder.
The expression in the last cell of the third column of the chart is equal to the decimal equivalent of 10%.
The total volume of solution is equal to the volume of bleach plus the volume of water.
1.10. Explore 6
Module 5: Rational Expressions
Using a chart like the one provided in Try This 4 is one strategy for setting up a rational equation to solve a problem. Charts are helpful for identifying patterns and organizing information. You probably also found the interactives Bleach Solution and Flyer Scramble useful.
Self-Check 3
The concentration, C, of salt in a solution is determined by the formula ![]() where A is the constant amount of salt, s is the initial amount of solution, and w is the amount of water added.
where A is the constant amount of salt, s is the initial amount of solution, and w is the amount of water added.
1.11. Connect
Module 5: Rational Expressions
Complete the Lesson 5 Assignment that you saved in your course folder at the beginning of this lesson. Show work to support your answers.
![]() Save your responses in your course folder.
Save your responses in your course folder.
Project Connection
Go to Module 5 Project: Dice Game Competition. Go to Part 3: Section 2 to play the game by rolling the dice three times and completing the chart.
Going Beyond
In this lesson you used tables to organize the information presented in a situation. Tables help you keep track of how pieces of information are related to one another. Logic grids can also manage large amounts of information.
The Law School Admission Test (LSAT) is a standardized exam that measures the aptitude of law-school applicants. In addition to reading comprehension and writing, the exam has an analytical reasoning section in which students solve logic problems. This section checks a person's ability to synthesize information, construct sound arguments, and draw logical conclusions.
© Salix Alba; Used under Creative Commons Licence 3.0- Share, Adapt, Attribution
Do you think you are ready for law school? Try to solve the next puzzle. You can also find this puzzle and others like it on the Internet.
Question: Five people have dinner reservations at a restaurant. Prior to going out for supper, each person completed his or her laundry and also went shopping. What time is each person’s reservation, what laundry product does each person use, and what item did each person purchase?
You may find it helpful to use Logic Grid to complete this activity.
Clue 1: The person who uses Sun didn’t buy the shoes.
Clue 2: The five people making reservations are the person who bought the scarf; the person with a reservation at 9:00 p.m.; Ayden; the person who uses Era; and the person who bought the shoes.
Clue 3: Either the person who uses Clorox or the person who uses Era is Hudson.
Clue 4: The person who uses Tide has a later reservation than Dalton.
Clue 5: Of the person who uses Era and Randy, one has the 6:00 p.m. reservation and the other bought the earrings.
Clue 6: Ayden has an earlier reservation than the person who uses Era.
Clue 7: The person with a reservation at 6:30 p.m. is not Hudson.
Clue 8: Dalton has a later reservation than the person who uses Biz.
Clue 9: The person with a reservation at 6:00 p.m. is Julius.
Clue 10: The person with a reservation at 5:30 p.m. bought the purse.
Search the Internet for other logic grid puzzles. Who knows? Maybe you will find yourself breezing through this section on the LSAT one day!
1.12. Lesson 5 Summary
Module 5: Rational Expressions
Lesson 5 Summary

Ryan McVay/Digital Vision/Thinkstock
In this lesson you investigated the following question: How can real-world problems be modelled with rational expressions and rational equations?
You explored three different types of problems that can be solved using rational equations, which included problems relating to motion, work, and proportions.
You saw how these types of problems are related to games in which members of each team compete against the clock to complete different events. You learned how to mathematically determine distance, speed, time, and proportion.
A key strategy in modelling these problems was to organize the important information. You learned how to use tables to keep track of the critical points of a situation. You then used the information to construct rational equations that could be solved for the desired quantity. Constructing equations was often based on known formulas.
You have now completed your study of rational expressions and equations. As you continue in your studies, you can be sure that you will encounter these concepts again. Remember that mathematics is a subject that continues to build on itself—what you have seen once before may be seen and applied again.