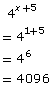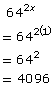Lesson 2
| Site: | MoodleHUB.ca 🍁 |
| Course: | Math 30-2 SS |
| Book: | Lesson 2 |
| Printed by: | Guest user |
| Date: | Wednesday, 24 December 2025, 6:22 AM |
Description
Created by IMSreader
1. Lesson 2
Module 7: Exponents and Logarithms
Lesson 2: Solving Exponential Equations
Focus
iStockphoto/Thinkstock
Bacteria are microscopic, single-celled organisms that can live almost anywhere. Escherichia coli, or E. coli, is a type of bacteria commonly found in the lower intestine of people. Most strains of E. coli are helpful, but some strains can cause food poisoning. In ideal conditions, in a Petri dish, E. coli will double in number approximately every 20 minutes. Exponential equations can be used to predict when the E. coli population will reach a given number.
In Lesson 1 you examined graphing exponential functions. In this lesson you will explore solving exponential equations.
Lesson Outcomes
At the end of this lesson, you will be able to
- determine the solution of an exponential equation in which the bases are powers of one another
- solve problems that involve loans and investments
Lesson Question
You will investigate the following question: How can exponential equations be used to solve problems involving growth and decay?
Assessment
Your assessment may be based on a combination of the following tasks:
- completion of the Lesson 2 Assignment (Download the Lesson 2 Assignment and save it in your course folder now.)
- course folder submissions from Try This and Share activities
- additions to Glossary Terms and Formula Sheet
- work under Project Connection
1.1. Launch
Module 7: Exponents and Logarithms
Launch
Do you have the background knowledge and skills you need to complete this lesson successfully? Launch will help you find out.
Before beginning this lesson, you should be able to simplify exponential expressions using exponent laws.
1.2. Are You Ready?
Module 7: Exponents and Logarithms
Are You Ready?
Complete these questions. If you experience difficulty and need help, visit Refresher or contact your teacher.
- Simplify the following expressions, leaving the answers with positive exponents.
Answer - Express each as a power with base 2.
- 16
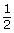
- 82
Answer
If you answered the Are You Ready? questions without difficulty, move to Discover.
If you found the Are You Ready? questions difficult, complete Refresher.
1.3. Refresher
Module 7: Exponents and Logarithms
Refresher
Use the “Exploring Laws of Exponents” activity to review the exponent laws. Click on each of the exponent laws to review them.
The laws of exponents can be used to manipulate expressions that include exponents.
Exponent Law |
General Case |
Product Law |
|
Quotient Law |
|
Power of a Power |
|
Power of a Product |
|
Power of a Quotient |
|
Zero Exponent Law |
|
Integral Exponent Law |
|
Go back to the Are You Ready? section and try the questions again. If you are still having difficulty, contact your teacher.
1.4. Discover
Module 7: Exponents and Logarithms
Discover
Try This 1
The equation for bacterial growth, starting with one bacterium, is P = 2t, where P is the number of bacteria and t is the number of 20-minute intervals.
| BACTERIA TABLE | |
| Number of 20-Minute Intervals That Have Passed | Number of Bacteria Present (P = 2t) |
| 0 | P = 20 = 1 |
| 1 | P = 21 = 2 |
| 2 | P = 22 = 4 |
| 3 | P = 23 = 8 |
| 4 | P = 24 = 16 |
- Determine how many 20-minute intervals would have passed if there are 64 bacteria? Explain how you found your answer.
-
- Use the equation P = 2t to determine the number of 20-minute intervals that would pass for there to be 256 bacteria. Explain how you found your answer.
- Describe how you could use a graphical method to solve the problem.
- Describe how you could use an algebraic method to solve the problem.
-
- Determine the number of 20-minute periods that would pass to produce 100 bacteria.
- Can you use a graphical method to solve the problem? Explain. Can you use an algebraic method? Explain.
![]() Save your responses in your course folder.
Save your responses in your course folder.
Share 1
With a partner or group, discuss the following questions based on your solutions in Try This 1.
- How did the various graphical methods compare?
- How did the various algebraic methods compare?
- Which method do you prefer? Explain.
![]() If required, place a summary of your discussion in your course folder.
If required, place a summary of your discussion in your course folder.
1.5. Explore
Module 7: Exponents and Logarithms
Explore
Hemera/Thinkstock
In Try This 1 you were working with an exponential equation. An exponential equation has a variable in the exponent. An example would be 5x = 25x − 1 because the variable x is an exponent.
In Try This 1 you attempted to solve the number of 20-minute intervals needed to produce a certain number of bacteria. You may have used an algebraic method or a graphical method to solve the problem. In Try This 2 you will try to solve exponential equations using an algebraic method.
One algebraic method you may have used in Try This 1 was writing each side of the equation as powers with the same base. To solve question 2, for example, 256 = 2t, you may have used a method similar to the following:
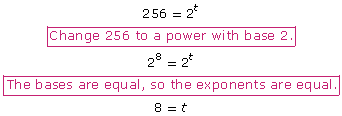
Notice from the example that if the bases of two equal powers are the same, then the exponents must be equal. Keep this important idea in mind as you complete Try This 2.
Try This 2
- Solve for x in the equation 4x = 64. Describe how you solved for the value of x.

- Solve for x in the equation 4x − 2 = 64. Describe how you solved for the value of x.

- Solve for x in the equation 4x + 5 = 642x. Describe how you solved for the value of x. Verify your solution.

![]() Save your responses in your course folder.
Save your responses in your course folder.
1.6. Explore 2
Module 7: Exponents and Logarithms
In Try This 2 you found that rewriting the powers on both sides of the equation to have the same base allowed you to determine the unknown variable in the exponent(s). If two powers are equal and their bases are equal, their exponents must also be equal. This can be expressed by the property that if bx = by, then x = y and b ≠ −1, 0, 1.
To use this property to solve exponential equations, there must be only one power on each side of the equation and the bases of the powers must be the same.
| Acceptable (Each side has one power and both powers have the same base.) |
Not Acceptable (Each side of the equation must have one power.) |
Not Acceptable (Bases must be the same on each side of the equation.) |
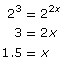 |
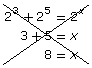 |
Sometimes, in order to change the base of a power, you must remember how to apply the exponent laws.
For example, in Try This 2 you solved 4x + 5 = 642x.

Verify your solution by substituting the value for x into the original equation.
| LS | RS |
|
|
| Left Side = Right Side | |
When entering powers into your calculator, use brackets around the exponent; for example, to enter 32x − 3 into your calculator, type 3, ^, (, 2, x, −, 3, ). Note that some calculators use xy to label the exponent button. Also, remember to be careful with negative values: (−2)^4 is different from −(2)^4.
The solution is x = 1.
Read “Example 2” on pages 355 to 357 of your textbook. Notice how exponent laws are used to combine powers so that there is a single power on each side of the equation and both powers have the same base.
Self-Check 1
Complete questions 4.a., 4.c., 7.a., and 7.b. on page 362 of the textbook. Answer
1.7. Explore 3
Module 7: Exponents and Logarithms
In Try This 2 you looked at solving exponential equations algebraically by writing each side of the equation with equivalent exponents that had the same base. In Try This 3 you will explore how to solve exponential equations graphically.
Try This 3
iStockphoto/Thinkstock
The medical isotope iodine-131 is produced at Chalk River Laboratories in Ontario and is used in imaging and diagnosing thyroid problems. A radioactive sample of iodine-131 has a half-life of 8 days. This means that after 8 days, half of the original amount of the sample has decayed.
The equation that can be used to describe the half-life function is
![]()
where A is the remaining mass of iodine-131, A0 is the original mass of iodine-131, and t is the time in days.
- Notice that in the function
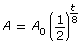 , the value of parameter b is
, the value of parameter b is 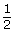 . Can you determine if this is exponential growth or exponential decay? Explain your reasoning.
. Can you determine if this is exponential growth or exponential decay? Explain your reasoning. 
- How long would it take a 4.0-g sample of iodine-131 to decay to 0.25 g?
- Determine the time algebraically.

- Determine the time using a graph. Describe the process you used.

- Determine the time algebraically.
![]() Save your responses in your course folder.
Save your responses in your course folder.
1.8. Explore 4
Module 7: Exponents and Logarithms
In Try This 3 you used a half-life equation to determine the time it takes for iodine-131 to decay specific amounts. View the Solving Exponential Equations presentation to see the example of how to solve the exponential equation ![]() by writing the equation so that the bases are powers of one another and then graphing a system of equations.
by writing the equation so that the bases are powers of one another and then graphing a system of equations.
Half-life is usually used to describe the length of time for a substance to decay to half the original amount, and can be described using the following formula:
![]()
In the formula, A is the final amount of the substance, A0 is the initial amount of the substance, t is the time elapsed, and h is the half-life of the substance.
The following example shows that it is possible to use this formula to model a decay that isn’t affected by time.
Read “Example 3” on pages 357 to 359 of the textbook to see a problem solved by using the same base and solved by graphing. Why might the textbook authors have used x instead of t in the half-life equation?
Self-Check 2
1.9. Explore 5
Module 7: Exponents and Logarithms
In Self-Check 2 you solved an exponential equation where each power could be expressed with the same base. How would you solve an equation when the bases cannot be changed to be the same?
For example, ![]() is difficult to solve using the same bases because 3 and 2(5) cannot easily be converted to the same base. One method to solve this equation is by using technology to find the solution graphically.
is difficult to solve using the same bases because 3 and 2(5) cannot easily be converted to the same base. One method to solve this equation is by using technology to find the solution graphically.
Read “Example 4” on pages 359 and 360 of the textbook to see how to solve exponential equations when the bases are not powers of one another. Notice how functions corresponding to each side of the equation are graphed to determine a solution. In this lesson, graphing will be used to solve equations that are difficult to convert to the same base.
Self-Check 3
Complete question 13 on page 364 of your textbook. Answer
1.10. Explore 6
Module 7: Exponents and Logarithms
There are different applications that use exponential functions. One of these areas is banking and finance. In Try This 4 you will use exponential equations to calculate investment values.
Try This 4

iStockphoto/Thinkstock
Are you saving money for something special? You might make that money grow faster if you invest it at a bank or with an investment firm. To calculate how much money you could accumulate, there are some formulas you can use that are based on exponential equations.
- Arthur invests $1000 at a rate of 3% per year. This means he will earn 3% of the amount in the account each year. Complete a table like the one that follows to to see how much money Arthur will accumulate after 6 years.1
3% COMPOUND INTEREST PER YEAR Year Starting Value Ending Value 0 $1000.00 $1000.00 + 0.03($1000.00) = $1030.00 1 $1030.00 $1030.00 + 0.03($1030.00) = $1060.90 2 $1060.90 $1060.90 + 0.03($1060.90) = $1092.73 3 4 5 6 - As you may have noticed from the table in question 1, the interest in year 2 is calculated not only on $1000 but also on the interest earned in year 1. That is why the interest is considered compounded. When you earn interest on principal and preceding interest earned, your money grows faster.
Instead of using a table to calculate the compound interest, you can use the compound interest formula.
The formula for compound interest is A = P(1 + i)n, where A is the amount of money at the end of the investment term; P is the principal, the original amount invested; i is the interest rate per compounding period, expressed as a decimal; and n is the number of compounding periods. The compounding period is the time during which interest is calculated on an investment.
Use this formula to confirm your answer for year 6 in the table from question 1. - Use the compound interest formula to calculate what the value of Arthur’s investment will be after 10 years and after 20 years. Add these values to your chart.
- Graph your compound interest formula.
-
- Use your graph to determine the amount of time for the investment to grow to $2000.
- Describe a method that you could use to answer question a. without using an exponential function. How long would this method take?
![]() Save your responses in your course folder.
Save your responses in your course folder.
1 From PRINCIPLES OF MATHEMATICS 12 by Canavan-McGrath et al. Copyright Nelson Education Ltd. Reprinted with permission.
1.11. Explore 7
Module 7: Exponents and Logarithms
In Try This 4 you used the formula A = 1000(1.03)n to simplify compound interest calculations. Typically, when repeated multiplication is used, an exponential function can be used to simplify the process. An exponential function can also be used to determine the length of time required to pay off a loan.
Read “Example 3” on pages 392 and 393 of the textbook. Although the equation is different from what you've worked with, the strategy for determining n is similar to what you have seen already.
Self-Check 4
- Complete question 11.a. on page 397 of the textbook. Answer
- A bandmaster borrowed $10 500 from a bank to buy new equipment, new lighting, and a new sound package. The interest rate on the loan is 3.6% per year, compounded monthly. The monthly payment on the loan is $400. The loan manager gives the bandmaster the following equation to determine how long it will take to pay off the loan:
(1.003)–n = 0.92 125, where n represents the number of months
Add exponential equation to your copy of Glossary Terms.
Add the following to your copy of Formula Sheet:
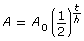
- A = P(1 + i)n
1.12. Connect
Module 7: Exponents and Logarithms
Complete the Lesson 2 Assignment that you saved in your course folder at the beginning of the lesson. Show work to support your answers.
![]() Save your responses in your course folder.
Save your responses in your course folder.
Project Connection
You are now ready to apply your understanding of exponential functions. Go to Part 1: Analyzing Data of the Module 7 Project: At the Movies. Complete Activity 1: Weekly Revenue.
1.13. Lesson 2 Summary
Module 7: Exponents and Logarithms
Lesson 2 Summary

iStockphoto/Thinkstock
In this lesson you explored how to solve exponential equations.
One method you studied was writing equivalent powers with the same base on both sides of the equal sign. Thus, the exponents are equivalent and you can then solve for an unknown exponent.
A second method was to solve using a graph. You graphed a system of equations and determined the solution by finding the x-value of the point of intersection of the two functions.
You explored how the compound interest formula could be used to determine how long you would need to invest money to have it grow to a certain amount or how long it would take to pay off a loan.
In future lessons you will learn an algebraic method of solving exponential equations when bases are not the same. In Lesson 3 you will explore the connection between exponential form and logarithmic form.