Lesson 3
| Site: | MoodleHUB.ca 🍁 |
| Course: | Math 30-2 SS |
| Book: | Lesson 3 |
| Printed by: | Guest user |
| Date: | Wednesday, 24 December 2025, 8:29 AM |
Description
Created by IMSreader
1. Lesson 3
Module 7: Exponents and Logarithms
Lesson 3: Converting Between Logarithms and Exponents
Focus
iStockphoto/Thinkstock
In Lesson 2 you explored exponential growth and decay. You may have noticed that exponential growth, such as in a population, can lead to very large numbers; and exponential decay, such as with a radioactive element, can lead to very small numbers.
In this lesson you will investigate logarithms and how they relate to exponents. Logarithms have many uses, one of which is to represent extreme values.
Lesson Outcomes
At the end of this lesson you will be able to
- convert from logarithmic form to exponential form
- convert from exponential form to logarithmic form
Lesson Question
You will investigate the following question: How are logarithms and exponents related?
Assessment
Your assessment may be based on a combination of the following tasks:
- completion of the Lesson 3 Assignment (Download the Lesson 3 Assignment and save it in your course folder now.)
- course folder submissions from Try This and Share activities
- additions to Glossary Terms and Formula Sheet
1.1. Discover
Module 7: Exponents and Logarithms
Discover

iStockphoto/Thinkstock
The Richter scale, named after the American geologist Charles F. Richter, is used to measure the amount of energy released, or magnitude, of an earthquake. According to the Geological Survey of Canada, more than 4000 earthquakes occur in Canada every year, but only about 50 of these earthquakes are felt by humans.
Earthquakes are measured by magnitude and amplitude, where magnitude is a number on the Richter scale and amplitude refers to the vibrations caused by the earthquake. Knowing the value of one helps determine the value of the other. The function used to determine the magnitude of an earthquake is y = log x, where y is the magnitude and x is the amplitude of the vibrations, which are measured by a seismograph.

Hemera/Thinkstock
A seismograph (the device in the top right) is used to measure the amplitude of earthquake vibrations.
Try This 1
- Using the function y = log10 x, complete a table like the following using a calculator. On the calculator you will use the log x button (the log x button refers to log10 x).
Amplitude of Vibrations (x units) x Substituted into the Logarithmic Equation
y = log10 xRichter Scale Magnitude (y) x Written as a Power with Base 10 1 y = log10 1 0 
100 y = log10 100 
10 000 y = log10 10 000 1 000 000 y = log10 1 000 000 -
- Describe the relationship you see between x, written as a power with base 10, and the value of y.
- Based on the relationship determined in a., predict the solution to y = log10 100 000 000. Use the log button on your calculator to check your prediction.
- When using the Richter scale, doubling the magnitude does not correspond to a doubling of the amplitude. Consider the amplitude when the magnitude is 4 and 8. How much larger is the amplitude for an earthquake with a magnitude of 8 than an earthquake with a magnitude of 4?
Share 1
With a partner or group, discuss the following questions based on your solutions in Try This 1.
- Without using a calculator, how else could you determine the magnitude in the table of Try This 1? Describe the patterns you saw in Try This 1. Explain how exponents and logarithms are related based on this information.
- Discuss what you think the subscript 10 means in log10.
![]() If required, save a summary of your discussion in your course folder.
If required, save a summary of your discussion in your course folder.
1.2. Explore
Module 7: Exponents and Logarithms
Explore

iStockphoto/Thinkstock
The notation log is used to indicate logarithm in mathematical expressions.
In Try This 1, in order to solve for the magnitude, y, given the amplitude, x, is 1, the logarithmic notation would be y = log10 1. Using your calculator you determined the answer is 0.
In Try This 1 you also saw that very large amplitudes could be described using much simpler, smaller numbers by taking the logarithms. Comparing earthquakes using the Richter scale numbers of 0, 1, 2, and so on is much simpler than comparing the amplitude numbers of 1, 10, 100, and so on. Think about how large some of the numbers on the following diagram would be if logarithms were not used.

From PRINCIPLES OF MATHEMATICS 12 by Canavan-McGrath et al. Copyright Nelson Education Ltd. Reprinted with permission. top photo: iStockphoto/Thinkstock; bottom photo: Stocktrek Images/Thinkstock
You may have also noticed a relationship between logarithms and exponents. In Try This 1 the value of the exponent was the same as the logarithm. Notice that the base of the exponent is the same as the base of the logarithm. In fact, a logarithm is an exponent.
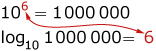
Using a more formal definition, a logarithm of a number is the exponent by which the base has to be raised to produce that number. The base of a logarithm is usually written as a small number. Bases other than 10 can be used, such as 3 in the diagram that follows.
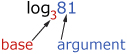
Logarithms have two parts to them. The small number is called the base and the large number is called the argument. Logarithms like this represent real numbers; for example, log3 81 = 4.
A logarithm with a base of 10, log10, is often written as just log without the base being written, and is called a common logarithm.
1.3. Explore 2
Module 7: Exponents and Logarithms
The patterns you have seen so far allow you to convert between exponents and logarithms.
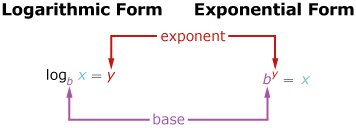
Source: Pre-Calculus 12. Whitby, ON: McGraw-Hill Ryerson, 2011.
Reproduced with permission. Reproduced with permission.
In Try This 2 you will convert between logarithmic and exponential form and investigate logarithms with bases other than 10.
Try This 2
- Complete a table similar to the following for y = log2 x.
Exponential Form
x = 10yLogarithmic Form
y = log10 x1 = 100 0 = log10 1 10 = 101 1 = log10 10 100 = 102 2 = log10 100 1000 = 103 3 = log10 1000 10 000 = 104 4 = log10 10 000
Exponential Form
x = 2yLogarithmic Form
y = log2 x1 = 20 0 = log2 1 2 = 21 
-
Convert the following expressions into logarithmic form.
- 10 000 000 = 107
- 64 = 26

- 243 = 35
- Convert the following expressions into exponential form.
- log10 1 000 000 = 6
- log2 256 = 8
- log17 118 587 876 497 = 9
![]() Save your responses in your course folder.
Save your responses in your course folder.
1.4. Explore 3
Module 7: Exponents and Logarithms
In Try This 2 you practised writing exponents as logarithms and practised writing logarithms as exponents for bases other than 10. You may have noticed that the base of an exponent was the same as the base of the logarithm.
Logarithms were invented independently by John Napier and Joost Bürgi in the early 1600s. Both used logarithms to help simplify multiplication and division. Pocket calculators have made this function obsolete; however, logarithms are still useful when solving exponential equations.

© Classic Image / Alamy
John Napier invented logarithms.

Joost Bürgi
Self-Check 1
- If the amplitude of vibrations in an earthquake is 1000, determine the resulting magnitude on the Richter scale. Use both the logarithmic notation, y = log10 x, and the exponential notation, x = 10y, to verify that they are equivalent forms. Answer
- Convert log3 81 = 4 to exponential form. Answer
- Convert 26 = 64 to logarithmic form. Answer
1.5. Explore 4
Module 7: Exponents and Logarithms
To determine the magnitude of an earthquake, the logarithmic notation y = log x was used, where the base was 10. This allowed the use of a calculator to determine the answer using the logarithmic function. When the base is not 10, evaluating logarithmic notation is problematic, and, therefore, using the exponential notation becomes useful.
Try evaluating log2 32 on your calculator. Did you get 1.505 14…? If you did, then you entered log 32 (log10 32). When entered in this way, the calculator assumes that the base is 10. One method to evaluate log2 32 is to use its equivalent exponential notation, 32 = 2y, and solve for y as follows:
32 = 2y
25 = 2y
Because the base is the same on both sides of the equal sign, the exponents must be equal; therefore, y = 5.
View Evaluating Logarithms for more examples of how to evaluate logarithms.
Self-Check 2
Evaluate each of the following logarithmic expressions.
1.6. Explore 5
Module 7: Exponents and Logarithms
Logarithms are used to measure things that can have extremely large or extremely small values, such as earthquake amplitude or magnitude, respectively. Along the same lines, logarithms are used to measure acidity of solutions. Have you ever tasted lemon juice or seawater? Lemon juice and seawater are known as solutions. Lemon juice is considered an acidic solution, and seawater is a basic or alkaline solution. Solution acidity is dependent on the concentration of hydrogen ions in the solution. The concentrations can be a very small number, so a pH scale is used to compare solutions’ acidity. The pH scale ranges from 0 to 14, as shown in the table.

From PRINCIPLES OF MATHEMATICS 12 by Canavan-McGrath et al. Copyright Nelson Education Ltd. Reprinted with permission.
Try This 3
A pH scale is used to measure the acidity of solutions, and pH can be found using p(x) = −log x, where x represents the concentration of hydrogen ions and is measured in moles per litre (mol/L).
Use the pH chart to help determine the hydrogen ion concentration of soapy water by filling in the following table.
| p(x) = − log x | |
| Substitute p(x) with the pH value for soapy water from the chart. | |
| Rewrite as an exponential equation. | |
Solve for x to find the hydrogen ion concentration. |
![]() Save your responses in your course folder.
Save your responses in your course folder.
1.7. Explore 6
Module 7: Exponents and Logarithms
Earlier, you saw that logarithms were useful when expressing very large numbers associated with earthquakes. Logarithms can also be useful when describing small numbers, such as the hydrogen concentration of a solution.
With earthquakes, the strength of the amplitude was calculated using the magnitude. You learned that even though the difference between magnitudes was small, the corresponding difference in amplitude was large. The acidity levels of different solutions can also be compared using a similar method.
Read “Example 6” on pages 433 and 434 of your textbook to see how logarithms can be used to compare the pH of solutions.
Self-Check 3
Complete “Your Turn” for “Example 6” on page 434 of your textbook. Answer
- logarithm
- base
- pH scale
- Richter scale
Add the following to your copy of Formula Sheet:
y = loga x ↔ ay = x
1.8. Connect
Module 7: Exponents and Logarithms
Complete the Lesson 3 Assignment that you saved in your course folder at the beginning of this lesson. Show work to support your answers.
![]() Save your responses in your course folder.
Save your responses in your course folder.
Project Connection
There is no Project Connection for this lesson.
1.9. Lesson 3 Summary
Module 7: Exponents and Logarithms
Lesson 3 Summary
In this lesson you learned about evaluating logarithmic expressions and the relationship between logarithmic notation and exponential notation in a variety of contexts.
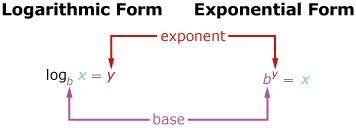
Source: Pre-Calculus 12. Whitby, ON: McGraw-Hill Ryerson, 2011.
Reproduced with permission. Reproduced with permission.
The logarithmic function y = logb x is equivalent to the exponential expression x = by. The value of a logarithm can be determined by letting the logarithm equal y, converting to exponential form, and then determining y. You cannot take the logarithm of a negative number. Logarithms are especially useful when working with numbers that are very large or very small, or that occur across a very large range.