Lesson 5
| Site: | MoodleHUB.ca 🍁 |
| Course: | Math 30-2 SS |
| Book: | Lesson 5 |
| Printed by: | Guest user |
| Date: | Wednesday, 24 December 2025, 4:26 AM |
Description
Created by IMSreader
1. Lesson 5
Module 7: Exponents and Logarithms
Lesson 5: Laws of Logarithms
Focus

© Samuel Borges/31276114/Fotolia
Most people can hear a wide range of sound levels. As the intensity of a sound increases, you perceive the sound as getting louder. It is possible to determine “how many times as loud” one sound is compared to another using the equation S = 10 log I1 − 10 log I0, where I1 and I0 are the two sound intensities. In this lesson you will learn to simplify logarithmic expressions such as this one.
Lesson Outcome
At the end of this lesson you will be able to use the laws of logarithms to manipulate expressions.
Lesson Question
You will investigate the following question: How can the laws of logarithms be used to manipulate expressions?
Assessment
Your assessment may be based on a combination of the following tasks:
- completion of the Lesson 5 Assignment (Download the Lesson 5 Assignment and save it in your course folder now.)
- course folder submissions from Try This and Share activities
- additions to Formula Sheet
- work under Project Connection
1.1. Discover
Module 7: Exponents and Logarithms
Discover
So far, you have seen that logarithms and exponents are closely related.

iStockphoto/Thinkstock

iStockphoto/Thinkstock
There are rules that can be used to combine powers with the same base. The next activity explores a related set of rules for logarithms.
Try This 1
- Complete a table like the following:

log 100 + log 1000 = 2 + 3 = 5 = log ____ 
log 10 + log 100 = = = log ____ log 10 000 + log 0.01 = = = log ____ -
- Explain any patterns you see in the table.
- Use your pattern to predict a rule for simplifying log M + log N.
- Check that your pattern works with numbers that are not powers of 10 by completing a table like the following using a calculator:
log 12 + log 3 = log 36 = log 5 + log 7 = log ____ = log 4 + log 9 = log ____ = -
Predict a rule for simplifying log M − log N.
-
Complete a table like the following using a calculator to test your rule:
log 18 − log 6 = log ____ = log 8 − log 2 = log ____ = log 10 − log 5 = log ____ =
![]() Save your responses in your course folder.
Save your responses in your course folder.
Share 1
With a partner or group, describe any patterns you see between the addition and subtraction rules for logarithms you developed in Try This 1 and the following exponent laws:
| (bm)(bn) = bm+n |
![]() If required, save a summary of your discussion in your course folder.
If required, save a summary of your discussion in your course folder.
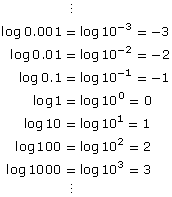
1.2. Explore
Module 7: Exponents and Logarithms
Explore

Adapted from Brand X Pictures/Thinkstock
In Discover, you may have found that logarithms can be added or subtracted using laws similar to
- log M + log N = log(M × N)
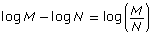
These rules can be extended to any base to give
- logb M + logb N = logb(M × N)
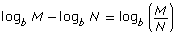
Notice that the bases must be the same to use these laws. The same restrictions apply to these rules as to other logarithms: b, M, and N are real numbers greater than 0, and b ≠ 1.
The following table provides an explanation of how the logarithmic laws are related to exponential laws. Remembering that a logarithm is an exponent may help you interpret the table.
Law of Logarithms |
Law Expressed Mathematically |
Pattern Explained by the Law of Powers |
| product law of logarithms | logb (M × N) = logb M + logb N | In the product law of powers, (bm)(bn) = bm + n, the exponents are added. In the product law of logarithms, logb (M × N) = logb M + logb N, when you are multiplying two terms in a single logarithm, it is the same as adding the logarithms of each term. |
| quotient law of logarithms | In the quotient law of powers, |
1.3. Explore 2
Module 7: Exponents and Logarithms
Read “Example 1” on pages 443 and 444 of your textbook to see a numeric example of the relationships described in the table.
The product and quotient laws of logarithms can be used to manipulate an expression into a different form. The following examples show how two logarithms can be combined into a single logarithm.
| log7 6 + log7 9 | The logarithms have the same base, so they can be combined. |
| = log7(6 × 9) | The logarithms are added, so use the product law of logarithms, logb (M × N) = logb M + logb N. |
| = log7 54 | Determine the product and write a single logarithm. |
| log3 72 − log3 8 | The logarithms have the same base, so they can be combined. |
| The logarithms are subtracted, so use the quotient law of logarithms, |
|
| = log3 9 | Determine the quotient and write a single logarithm. |
| = 2 | This logarithm can be evaluated to a whole number. |
The process shown in the examples can be reversed to write a logarithm as two separate logarithms, as shown in the following examples:
log5 (8 × 12) = log5 8 + log5 12
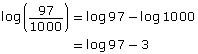
Self-Check 1
- Complete questions 1.a., 2.b., 3.a., 4.b., 6.b, 6.c., 8.b., and 14 on pages 446 and 447 of your textbook. Answer
1.4. Explore 3
Module 7: Exponents and Logarithms
So far, you have seen the product and quotient laws of logarithms. There is a third law that is commonly used with logarithms. The next activity explores this rule.
Try This 2
- Complete a table like the following:
log 2 = log 21 = 1 × log 2 = log 4 = log 22 = 2 × log 2 = log 8 = log 23 = 3 × log 2 = log 16 = log 24 = 4 × log 2 = -
- What pattern do you notice from the table?
- Use your rule to predict an alternate way of writing log 54.
- Use your rule to predict an alternate way of writing 6 log 2.
- Does your rule work for other bases, such as log4? Explain.
![]() Save your responses in your course folder.
Save your responses in your course folder.
Share 2
With a partner or group, describe any patterns you see between your rule from Try This 2 and the exponent law (bm)n = bm × n.
![]() If required, save a summary of your discussion in your course folder.
If required, save a summary of your discussion in your course folder.
1.5. Explore 4
Module 7: Exponents and Logarithms
In Try This 2, you may have found that the logarithm of a power can be rewritten as the product of a number and a logarithm using the law logb (Mn)= n logb M. The following explains the relationship between this law and the power law of powers:
| power law of logarithms | logb (Mn)= n logb M | In the product law of powers, (bm)n = bm × n, the exponents are multiplied. In the power law of logarithms, logb (Mn)= n logb M, when you have a power in a single logarithm, it is the same as multiplying the exponent to the logarithm of the base of the power. |
One way of thinking of the rule logb (Mn)= n logb M is that the value n can be moved from the exponent position to become the coefficient of the log and vice versa.
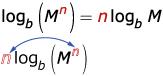
Here are some numeric examples of the power law of logarithms:
log6 24 = 4 log6 2
The power law of logarithms is useful when trying to solve exponential equations. Lesson 6 will explore this idea.
Self-Check 2
Add the following to your copy of Formula Sheet:
- logb M + logb N = logb(M × N)
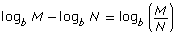
- logb (Mn) = n logb M
1.6. Connect
Module 7: Exponents and Logarithms
Complete the Lesson 5 Assignment that you saved in your course folder at the beginning of this lesson. Show work to support your answers.
![]() Save your responses in your course folder.
Save your responses in your course folder.
Project Connection
You are now ready to apply your understanding of the exponent laws. Go to the Module 7 Project: At the Movies. Complete Part 2: Logarithmic Scale.
Going Beyond

iStockphoto/Thinkstock
Before pocket calculators were invented, the product and quotient laws of logarithms and a table of logarithms were used to estimate the product or quotient of very large or very small numbers.
For example, to multiply 1298 × 4511, you could do the following:
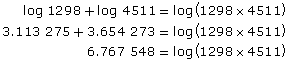
Use the Logarithmic Table to look up the number whose logarithm is 6.767 548.
5 855 284 ≈ 1298 × 4511
- The preceding example uses values rounded to six decimal places. How accurate of an estimate is this? How could you improve the accuracy?
- Why is using a table of logarithms easier than multiplying or dividing very large or very small numbers by hand?

iStockphoto/Thinkstock
A slide rule includes a condensed logarithmic table and can be used to multiply and divide very large or very small numbers. A version of the slide rule was invented in the 1620s shortly after logarithms. Slide rules were commonly used until the 1970s. It is likely that either your parents or grandparents used a slide rule in their math classes.
1.7. Lesson 5 Summary
Module 7: Exponents and Logarithms
Lesson 5 Summary
In this lesson you learned the following three laws of logarithms:
- logb M + logb N = logb(M × N)
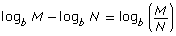
- logb (MN) = n logb M
These laws can be used to manipulate expressions to a more desirable form. In the next lesson you will see how these can be used to help solve exponential equations.