Lesson 6
| Site: | MoodleHUB.ca 🍁 |
| Course: | Math 30-2 SS |
| Book: | Lesson 6 |
| Printed by: | Guest user |
| Date: | Wednesday, 24 December 2025, 4:31 AM |
Description
Created by IMSreader
1. Lesson 6
Module 7: Exponents and Logarithms
Lesson 6: Solving Exponential Equations Using Logarithms
Focus
iStockphoto/Thinkstock
Now that you have learned the power law of logarithms, you can use the law to solve exponential equations. This means you can determine an exact value of t in equations like the E. coli growth equation you saw in Lesson 2. In this lesson you will learn how to solve exponential equations by applying the laws of logarithms.
Lesson Outcome
At the end of this lesson you will be able to solve exponential equations using logarithms.
Lesson Question
You will investigate the following question: How can logarithms be used to solve exponential equations?
Assessment
Your assessment may be based on a combination of the following tasks:
- completion of the Lesson 6 Assignment (Download the Lesson 6 Assignment and save it in your course folder now.)
- course folder submissions from Try This and Share activities
- work under Project Connection
1.1. Discover
Module 7: Exponents and Logarithms
Discover

iStockphoto /Thinkstock
In this activity you will determine the time when the bacteria reach a certain population using the equation ![]() of the laws of logarithms.
of the laws of logarithms.
Try This 1
Suppose that you begin with a single E. coli bacterium at time 0, and the conditions are appropriate for the bacteria to double in population every 20 min. This growth can be modelled using the equation ![]()
-
- Create a table that shows the number of bacteria at 20-min intervals for 5 h. Your table might start out like this one.
Time (in min) Number of Bacteria 0 20 40 - Use your table to estimate when there would be 10 000 bacteria.
- Create a table that shows the number of bacteria at 20-min intervals for 5 h. Your table might start out like this one.
-
- Follow the steps in the following table to algebraically determine an approximate time when there would be 10 000 bacteria. Make the assumption that the equation
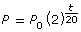 can be used to find an approximate time where there would be 10 000 bacteria.
can be used to find an approximate time where there would be 10 000 bacteria.
Write the equation. 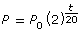
Substitute the known values for P and P0. 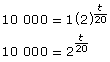
Take the logarithm of both sides of the equation. 
Use the power law of logarithms, logb (Mn) = n logb M, to “bring down” the exponent 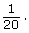
Divide both sides of the equation by log 2. Multiply both sides of the equation by 20. Determine a decimal approximation of t. - How does the time you determined in 2.a. compare to your estimate from 1.b.?
- Follow the steps in the following table to algebraically determine an approximate time when there would be 10 000 bacteria. Make the assumption that the equation
![]() Save your responses in your course folder.
Save your responses in your course folder.
Share 1
With a partner or group, discuss the following based on your responses in Try This 1.
- Explain why the power law of logarithms is necessary to solve many exponential equations.
- How accurate do you expect the prediction you made in question 2.a. to be? Explain why.
![]() If required, save a summary of your discussion in your course folder.
If required, save a summary of your discussion in your course folder.

© Joe Gough/39773088/Fotolia
Most types of E. coli are harmless, or even helpful, to people. However, some strains of E. coli can cause food poisoning. One of the most common sources of these pathogenic E. coli is in undercooked ground beef. This is one reason why meat producers suggest cooking hamburger to 71°C before eating it.
1.2. Explore
Module 7: Exponents and Logarithms
Explore
In Try This 1 you looked at a method for solving exponential equations using logarithms. Using the same conditions as in Try This 1, the time it takes for there to be 500 000 bacteria is determined by using the following equation. Notice when the power law of logarithms is used.
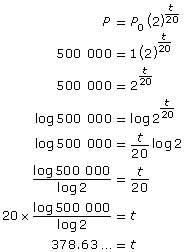
Read “Example 2” on pages 450 and 451 of your textbook if you would like to see another example of how an exponential equation can be solved using logarithms.
Self-Check 1
![]()
- Complete “Check Your Understanding” questions 1.a., 1.b., and 1.e. on page 455 of your textbook. Answer
- Complete Solving Exponential Equations 1.

1.3. Explore 2
Module 7: Exponents and Logarithms
| Incorrect Use of Logarithms | Correct Use of Logarithms |
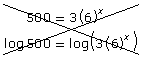 |
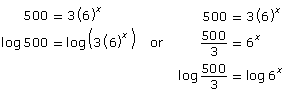 |
Also, when using the power law of logarithms, the logarithm must be of just the power. Continuing the example, consider the following table:
| Incorrect Use of Power Law of Logarithms | Correct Use of Power Law of Logarithms |
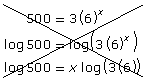 |
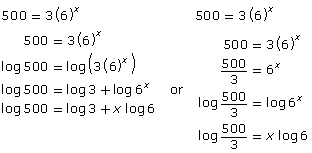 |
Read “Example 3” on pages 451 to 453 of your textbook. Notice that when logarithms are used, they are used on the entirety of both sides of the equation.
Self-Check 2
1.4. Explore 3
Module 7: Exponents and Logarithms
Sometimes an exponential equation will have more than one power in it. Solving these equations follows a process similar to the exponential equations you saw earlier. In Try This 2, you will explore how to solve this type of equation.
Try This 2
Open and complete Solving Exponential Equations 2.
1.5. Explore 4
Module 7: Exponents and Logarithms
Watch Solving Exponential Equations with Two Powers to see how an exponential equation with multiple powers, similar to the one you saw in Try This 2, can be solved.
When working with logarithms, it can be useful to change the base of the logarithm. Some calculators will not accept most bases, so converting to base 10 allows you to determine a decimal approximation. In Try This 3 you will explore a method that can be used to convert between bases.
Try This 3
- Consider the equation y = log4 20. Complete the following steps to give an expression of y using base-10 logarithms.
Write the original logarithm. y = log4 20 Rewrite the logarithm in exponential form. 
Take the base-10 logarithm of each side of the equation. Use the power law of logarithms, logb (Mn) = n logb M, to “bring down” the exponent y.
Divide both sides by log 4 to isolate y. - Compare the resulting expression with the initial expression in question 1. Describe a rule showing how logb x can be rewritten using a different base.
![]() Save your responses in your course folder.
Save your responses in your course folder.
1.6. Explore 5
Module 7: Exponents and Logarithms
In Try This 3, you may have found that the base of a logarithm can be changed using a formula equivalent to ![]()
Self-Check 3
1.7. Explore 6
Module 7: Exponents and Logarithms
When a problem is modelled using an exponential equation, it is often useful to solve that equation using logarithms. In Try This 4, you will solve a problem involving compound interest.
Try This 4

iStockphoto/Thinkstock
When a bank sets a rate for an investment or a loan in Canada, the prime rate set by the Bank of Canada is often used as a guideline. In 1981, the prime rate reached 22.75%, and, in 2009, it dipped to 2.25%. Compare the time it takes an investment to increase using these two rates by completing the following questions.
- Imagine depositing $1000 into a bank account that paid compound interest at 2.25% per year and $1000 into one that paid 22.75% per year. Write an exponential equation to represent the amount of money in each account after t years.

- How much money would each account have after 5 years?
- Determine how long it would take for each account to accumulate $5000 by solving the equations using logarithms.

- Typically, extreme interest rates like these don’t last for very long. How would this change your expectation for the length of time taken for $1000 to grow into $5000?
![]() Save your responses in your course folder.
Save your responses in your course folder.
1.8. Explore 7
Module 7: Exponents and Logarithms
In Try This 4 you may have found that it takes nearly 10 times as long for an investment at 2.25% to grow to 5 times its original amount than an investment at 22.75%. These rates are extreme, and most mortgage rates and savings-account rates would fall somewhere between them.
To see another example of how logarithms can be used to solve a financial problem, read “Example 1” on pages 449 and 450 of your textbook. As you read, note how rounding errors are minimized by rounding only the final answer.
Self-Check 4
Complete questions 7, 9, 10, and 14 on pages 456 to 458 of your textbook. Answer
Add the following to your copy of Formula Sheet:
1.9. Connect
Module 7: Exponents and Logarithms
Connect
Lesson 6 Assignment
Complete the Lesson 6 Assignment that you saved in your course folder at the beginning of this lesson. Show work to support your answers.
![]() Save your responses in your course folder.
Save your responses in your course folder.
Project Connection
You are now ready to apply your understanding of logarithmic functions. Go to Part 3: Research Movie Revenues of the Module 7 Project: At the Movies. Complete Activity 1: Solving an Exponential Equation.
1.10. Lesson 6 Summary
Module 7: Exponents and Logarithms
Lesson 6 Summary
In this lesson you explored a new way of solving an exponential equation that used logarithms. Taking the logarithm of each side of the equation and then using the power law for logarithms is a good way to solve exponential equations that cannot be solved easily using common bases.
Sometimes it is useful to change the base of a logarithm. The equation ![]() can be used to accomplish this.
can be used to accomplish this.

