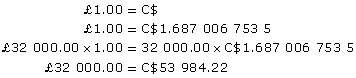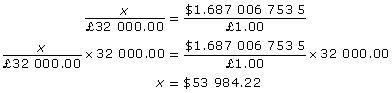Module 8
| Site: | MoodleHUB.ca 🍁 |
| Course: | Biology 30 [5 cr] - AB Ed copy 1 |
| Book: | Module 8 |
| Printed by: | Guest user |
| Date: | Thursday, 18 September 2025, 4:18 PM |
Description
Created by IMSreader
Table of contents
- 1. Module 8
- 1.1. Lesson 1
- 1.2. Page 2
- 1.3. Page 3
- 1.4. Page 4
- 1.5. Page 5
- 1.6. Lesson 2
- 1.7. Page 2
- 1.8. Page 3
- 1.9. Page 4
- 1.10. Page 5
- 1.11. Page 6
- 1.12. Lesson 3
- 1.13. Page 2
- 1.14. Page 3
- 1.15. Page 4
- 1.16. Page 5
- 1.17. Page 6
- 1.18. Lesson 4
- 1.19. Page 2
- 1.20. Page 3
- 1.21. Page 4
- 1.22. Page 5
- 1.23. Page 6
- 1.24. Lesson 5
- 1.25. Page 2
- 1.26. Page 3
- 1.27. Page 4
- 1.28. Page 5
- 1.29. Lesson 6
- 1.30. Page 2
- 1.31. Page 3
- 1.32. Page 4
- 1.33. Page 5
- 1.34. Lesson 7
- 1.35. Page 2
- 1.36. Page 3
- 1.37. Page 4
- 1.38. Page 5
- 1.39. Page 6
- 1.40. Module 8 Summary
1. Module 8
Module 8: Daily Living
Module 8 Introduction

© Tupungato/4145828/Fotolia
Have you considered how interdependent Canadians are? Whether you live in a rural community or in the city, whether you live along the American border in Canada’s South or in Canada’s North, many of the items you rely on have been transported great distances to get from where they were grown or manufactured to where you live. Goods also travel outside of Canada. Many Canadians are dependent on exporting their products to the United States and other countries.
Each person has a role to play in this web of interdependence—from the grocer who stocks the shelves in the local store, to the banker without whom commerce would grind to a halt, to the trucker who hauls the goods to your community. There are many occupations and careers you could choose from this interwoven web; each career makes an important contribution!
In Module 8 you will explore the cost of goods and how goods are priced. You will examine ways of saving money by comparing prices. You will also discover how the relative values of foreign currencies are used in international trade and commerce. These tools are part of daily living and making your income go further.
As you move further through Module 8, you will explore different ways income is paid in various occupations. You will investigate the advantages and disadvantages of each method of earning income, so that you can make informed choices in the future. You will also explore deductions from your pay—taxes, pension-plan contributions, and employment insurance. Canada uses the money collected through deductions from you paycheque to provide opportunity and support to all Canadians.
In Module 8 you will investigate the following questions:
How does an understanding of unit pricing and currency exchange help in your daily life?
What are the various ways income is earned and deductions from pay are calculated?
Once you have completed this module, you should have the skills necessary to complete the Unit 4 Project. Make sure you take a moment now to skim the Unit 4 Project, so that you know what to expect.
Save a copy of the Module 8 Glossary in your course folder now.
The Module 8 Glossary is a list of all of the new terms you will see in the lessons. Each time you see a definition, open your copy of the Glossary. Use the space available to add notes or drawings to help your understanding. You will be able to use your personal Glossary as a study tool.
1.1. Lesson 1
Module 8: Daily Living
Lesson 1: Unit Prices
Focus

© Monkey Business/17001074/Fotolia
Mila owns a health-food store in a city close to where Anna lives. Mila is always so welcoming and helpful when Anna shops at the store that Anna is considering interviewing Mila about her career. Anna wants to know why Mila chose to work in retail.
Anna has just dropped into the store to buy some 500-mg tablets of vitamin C. Anna holds up two containers of tablets. “It costs $8.99 for 200 tablets and $18.99 for 500 tablets. Which container is the better buy?” Anna asks.
“Generally, the larger size is less expensive,” Mila says, “but not always!” Bring the containers to the counter, and I’ll use my calculator to check. Also think about whether you would use all 500 tablets before they expire.”
Which container would you buy?
Lesson Questions
In this lesson you will explore the following questions:
How are unit prices calculated?
How do you determine the best buy if unit price, quality, and quantity are all factors you must consider?
How do retailers express the price of items they wish to promote?
Assessment
You will complete the Lesson 1 Assignment Booklet for assessment. Download the Lesson 1 Assignment Booklet and save it in your course folder now. You will receive instructions on how to complete the Assignment Booklet later in the lesson. You will also be prompted to start working on the Unit 4 Project.
There are other activities that you will complete throughout this lesson. It is important to complete all activities and save them in your course folder. Your teacher may ask to see your work at any time.
The lesson provides you with opportunities to investigate, review examples, and practise the knowledge and skills you are learning. In Self-Check activities you can compare your answers to see if you are on track. If you are having difficulty with concepts or calculations, contact your teacher.
Required Materials and Equipment
You will need your calculator and your problem-solving skills.
1.2. Page 2
Module 8: Daily Living
Get Started

© Joss/125996/Fotolia
You are craving chocolate! You find the candy aisle and see two large bars of milk chocolate. Each bar costs $5.00, but one weighs 1 lb and the other is 480 g. You like both of the brands equally. How do you figure out which chocolate bar is the best deal?
It’s tricky to compare the chocolate bars to see which is the better deal when their weights are in different units. Do you remember how to convert between pounds and kilograms? The mental math technique that follows can be a convenient and quick way to figure out the best deal.

© appler/2670895/Fotolia
If you are home and close to the fridge, check to see if there is a 1-L container of milk or juice. Remember, the mass (weight) of a 1-L container is very close to 1 kg. Lift the container to remind yourself what a 1-kg mass feels like to pick up.

© Robert Spriggs/10048016/Fotolia
If there is a package of butter, you will probably see that it is marked as weighing 454 g. That is because, traditionally in Canada, butter was sold by the pound. One pound is equal to 454 g.
Remember,
1 lb = 453.592 368 84 . . . g
1 kg = 2.204 622 622 . . . lb
In most instances, especially when doing mental calculation in the grocery store, it is easier to use the approximation ![]()
How do you quickly convert from kilograms to pounds?
Think about butter. How many pounds of butter are in 1 kg?

© Robert Spriggs/10048016/Fotolia
In the image shown you see that 1 kg is equal to 2 lb plus 20% of a pound.
1 kg = 1 lb + 1 lb + 20% of 1 lb
1 kg = 2.2 pounds
Example 1
Approximately how many pounds are there in 15 kg?
Solution
Method 1: Calculator
Multiply by 2.2.
![]()
Method 2: Mental Calculation (without using a calculator)
To convert to pounds, you would multiply by 2.2. The calculation is simpler if you break it down into three steps.
Step 1
15 × 2 = 30 lb
You will notice this step gets you close to the calculated answer of 33 lb shown in Method 1. You could stop here and have a good estimation. To get an even better estimation, continue to Step 2.
Step 2
Find 0.2 of 15 (or 20% of 15).
Take 10% of 15. (Hint: Move the decimal to the left one place.)
10% of 15 = 1.5
Since you need 20%, double the number.
1.5 + 1.5 = 3.0
3.0 is 20% of 15.
Step 3
Add the results of Step 1 and Step 2 together.
30 + 3 = 33
![]()
Keep this in mind: 2 × number of kilograms + 0.2 × number of kilograms = 2.2 × number of kilograms.
 Self-Check
Self-Check
Use both methods from Example 1 to estimate the number of pounds in each question.
SC 1. 40 kg = ? lb
SC 2. 4.5 kg = ? lb
SC 3. 6 kg = ? lb
SC 4. 35 kg = ? lb
1.3. Page 3
Module 8: Daily Living
Explore

© Nataliya Hora/15017382/Fotolia
In many grocery stores there is an aisle that sells bulk foods. Items such as candies, nuts, spices, baking ingredients, dried fruits, cookies, and dried cereals are in large containers from which customers serve themselves. The same items are also sold in packages elsewhere in the store. Often, but not always, the same items sold in packages are more expensive. In the bulk aisle, prices are commonly expressed per 100 g. The following example will show a method you can use to compare items sold in packages to items sold in bulk.
An example is given as an illustration of what is expected.
Example 2
Skyler can buy baking almonds from the bulk bins for $0.99/100 g. He can also purchase a 250-g package of almonds for $7.99. Which is the better buy?
Solution
View the animated “Example 2 Solution: Unit Price Solution.”
 Self-Check
Self-Check
In this question you will convert prices between pounds and kilograms.
SC 5. Kim finds jellybeans at the local supermarket. Help Kim decide which jellybeans are the better deal: those from the bulk bin, which sell for $0.49/100 g, or the 150-g package, which sells for $1.39.
 Try This
Try This
In this activity you will explore the difference in price between at least five items sold in bulk and the same five items sold in 100-g packages.
Prepare: Make a trip to your local grocery store or look on the Internet to find prices to complete a table like the one that follows. Record prices from five items in the bulk aisle. Then find the prices of equivalent prepackaged goods. Remember to record the prepackaged weights.
TT 1. Complete a table like the following. An example has been done for you. Round calculated prices to the nearest cent.
|
Item |
Bulk Price/100 g |
Package Size |
Package Price |
Package Price/100 g |
|
baking almonds |
$0.99/100 g |
250 g |
$7.99 |
$3.20/100 g |
|
a. |
|
|
|
|
|
b. |
|
|
|
|
|
c. |
|
|
|
|
|
d. |
|
|
|
|
|
e. |
|
|
|
|
TT 2. Were any packaged items cheaper than the equivalent bulk items?
TT 3. Even if more expensive, why do some consumers prefer to buy packaged items?
TT 4. Look on the Internet for cost-comparison calculators, which may assist in checking your table entries. There are a number of cost-comparison calculators available for both the computer and cellphone. Search the web for the best calculators, and be prepared to share these with other students. And, of course, you may use one of these calculators in the future to guide your own shopping!
 Share
Share
Share your answers to TT 1 to TT 4 with a partner or group. Focus your discussion on TT 2. Discuss the advantages and disadvantages of buying prepackaged items. What are the advantages of buying items in bulk, other than just the lower cost? What might some disadvantages be?
Summarize this discussion in a paragraph and save a copy in your course folder for future reference.
1.4. Page 4
Module 8: Daily Living
Bringing Ideas Together
In Explore you compared prices using 100 g as the comparison “unit.” This means you had each item as a price per 100 g in order to determine the best price. When an item’s cost is written as a cost per unit, the cost is referred to as a unit price.
If you are calculating unit prices for items sold by weight, then the comparison unit could be 1 lb, 1 kg, 100 g, or even 1 g. The comparison unit you use depends on the context and on what gives you a reasonable answer. A price of $1.31/kg, for instance, is more understandable than a price of $0.001 31/g, although both prices are the same.
If items are sold by volume, you might use 1 L as the comparison unit, or 100 mL, or even 1 mL. And, if you were in the United States, you will see quarts and gallons used as comparison units as well.
Work through these examples.
Example 3
In Canada, prices of fruits and vegetables are often posted in the store per pound. The per-kilogram price is often on the sticker in a much smaller print size. However, if you look at your cashier’s receipt, the prices will be printed per kilogram.
At the local supermarket, bananas are advertised at $0.59/lb. Estimate the price per kilogram. Round to the nearest cent.
Solution
Remember that ![]()
1 lb costs $0.59.
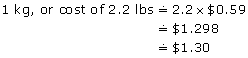
Bananas cost $1.30/kg.
Mental Math
If you did not have a calculator, you could mentally calculate the price per kilogram using the approach outlined in Get Started.
First round the price to 60¢/lb. Multiply by 2.
2 × 60¢ = 120¢
Take 20% of 60¢ by finding 10% and then doubling. You know that 10% of 60¢ is 6¢. To find 20%, double 6¢, which is 12¢.
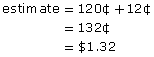
This mental estimate is 2¢ too high because you rounded up a penny and then doubled. By subtracting 2¢, you get the same answer: $1.30/kg.
 Self-Check
Self-Check
In the following questions you will convert prices between pounds and kilograms.
SC 6. Devan is flipping through a grocery flyer. He sees T-bone steak advertised for $4.99/lb.
- What is the price per kilogram?
- How would you mentally estimate the price per kilogram?
- Why do you think the price is advertised per pound rather than per kilogram?
SC 7. Penny is checking her receipt from her recent trip to the grocery store. She remarks that the chicken thighs she purchased cost $4.38/kg. What would have been the price per pound advertised at the store?
Prices per 100 mL or 100 g
Some prices are given not per kilogram or per litre but per 100 g or per 100 mL. Study the following examples to see why.
Example 4
A specialty sausage in the deli department of a local supermarket is advertised for $2.69/100 g.
- What is the price per kilogram?
- What is the price per pound?
- Give a reason why the price might be quoted in $/100 g?
Solution
- Remember, there are 1000 g in a kilogram. Since 10 × 100 g = 1000 g, a kilogram is 10 times as large as 100 g.
100 g cost $2.69. So, 1 kg costs 10 × $2.69 = $26.90.
- Remember,
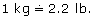 1 kg costs $26.90.
1 kg costs $26.90.
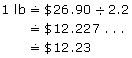
One pound costs $12.23.
- The deli uses 100 g because $2.69/100 g looks much less expensive than either $26.90/kg or $12.23/lb.
Example 5
The local supermarket displays unit prices for its canned goods, such as soups, to the nearest tenth of a cent per 100 mL. A 284-mL can of tomato soup sells for $0.49. What is the unit price the store would display on the shelf?
Solution
$0.49 = 49¢
Set up a proportion. Let x be the price per 100 mL.
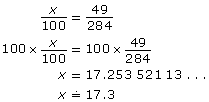
The unit price label reads 17.3¢/100 mL.
In the next set of questions you will use unit prices to see which item is the better buy.
 Self-Check
Self-Check
SC 8. At the same supermarket as in Example 5, a competitor’s brand of tomato soup is sold in a 300-mL can for $0.55.
- What unit price is shown for this brand?
- Based on price alone, which brand of soup is the better buy: the soup from Example 5 or the soup in this question?
SC 9. Still at the same supermarket, Eldon is checking the unit prices to compare the same brand of breakfast cereal sold in two different sizes. The 685-g package sells for $3.29, and the 1.9-kg box sells for $9.99. Based on the unit prices shown in ¢/100 g, which is the better buy?
SC 10. A certain brand of dishwasher soap at the local general store is sold in two sizes. The 1.69-kg size retails for $5.79, and the 2.83-kg size sells for $8.49. Determine the better buy by calculating the unit price in dollars per kilogram. Round to the nearest cent.
SC 11. A popular bathroom tissue comes in two sizes: a 16-roll size that sells for $8.79, and a 24-roll size for $10.49. Calculate the price per roll to determine which is the better buy. Round the price per roll to the nearest tenth of a cent.

© 2009 Royal Canadian Mint – All Rights Reserved
 Mastering Concepts
Mastering Concepts
This is a photo of a Canadian 1-oz gold coin. The Royal Canadian Mint manufactures 1-oz gold coins for investors. The Mint also has minted gold coins with a mass of 1 kg. Precious metals are quoted in dollars per troy ounce. A troy ounce is 31.103 466 8 g.
On January 31, 2010, the price of gold was C$1156.83/oz. On that date, how much was 1 kg of gold worth?
1.5. Page 5
Module 8: Daily Living
Lesson Summary
When shopping, it is important to consider the price of items as well as their appearance, quality, freshness, or brand. In Lesson 1 you explored strategies for comparison shopping. As well, you investigated how retailers often price articles to enhance sales.
In this lesson you explored three questions:
How are unit prices calculated?
How do you determine the best buy if unit price, quality, and quantity are all factors you must consider?
How do retailers express the price of items they wish to promote?
Check your level of understanding of the materials covered in this lesson by completing “Lesson 1 Traffic Lights.”
If you select an amber or red traffic light in the multimedia piece, you will receive information about additional work you can complete to improve your understanding of the topics. Complete the suggested work before you proceed to the Lesson 1 Assignment. If you experience difficulty, contact your teacher before starting the Lesson 1 Assignment.
In this lesson you analyzed unit prices in both SI and imperial measures, as it is still common in Canada. You saw that meats and produce are advertised in price per pound, even though, at the cash register, the prices are quoted in metric measures.
 Assignment
Assignment
Retrieve the Lesson 1 Assignment Booklet you saved in your course folder at the start of this lesson. Complete the Assignment Booklet. Resave your Assignment Booklet in your course folder and submit a copy to your teacher for assessment.
Unit 4 Project
Before you move on to the next lesson, make sure you have reviewed the Unit 4 Project. You should have a good idea of what is expected in the Unit 4 Project. Think of the career or job you would like to explore. Also think of potential people in that career or job you might interview.
1.6. Lesson 2
Module 8: Daily Living
Lesson 2: Price Increases and Decreases
Focus

© alaettin yildirim/
14619408/Fotolia
Mike’s mother wants new winter tires installed on her vehicle. She has asked Mike to check out prices. Mike has just stopped by the shop where his friend Carmen works. Carmen says they have a mid-season special right now. Snow tires the size Mike’s mother needs are regularly $199.00 each; but, if she purchases the tires this week, she will get all four tires for the price of three. Mike knows that, at the local building centre, the same tires are regularly $209.00 apiece, but they are on sale right now for 30% off.
Which is the better buy?
Mike likes the idea of working at a shop like Carmen’s. He wonders how much Carmen earns and how the shop sets its tire prices.
Lesson Questions
In this lesson you will explore this question:
How are percentages used to calculate discounts, mark-ups, and sales taxes?
Assessment
You will complete the Lesson 2 Assignment Booklet for assessment. Download the Lesson 2 Assignment Booklet and save it in your course folder now. You will receive instructions on how to complete the Assignment Booklet later in the lesson. You will also be prompted to continue working on the Unit 4 Project.
Remember to save all activities, including those that are not part of the Assignment Booklet, in your course folder.
Required Materials and Equipment
You will need a few sales flyers (online flyers will work too), your calculator, and your problem-solving skills.
1.7. Page 2
Module 8: Daily Living
Get Started

© TheSupe87/11562662/Fotolia
Find a couple of sales flyers that have arrived in the mail or that are available online. Take a few minutes to leaf through the flyers. Focus on how the consumer is encouraged to make purchases from the stores advertising in the flyers.
Are the flyers attractive and well laid out, and do the flyers highlight items of interest? Are there items on sale for less than regular price? Are percent discounts featured or are the dollar values of the discounts displayed? How can you tell, for instance, if $10.00 off is as good as a discount of 20%?
Percents
percent: out of a hundred
The symbol for percent is %.
Did You Know?
The percent symbol, %, is just a shorthand way for writing /100.
When you are working with percents, an important skill is being able to convert among percents, decimals, and fractions.
 Self-Check
Self-Check
Work with a partner, if possible. Explore Conversions. Save this table of percents, fractions, and decimals in your course folder.
The first two rows have been completed for you. Do you see the pattern of how the representation of values changes between a percent, a fraction, and a decimal?
SC 1. to SC 3. Fill in the empty squares in the table using the patterns you discovered.
Conversions
|
Question |
Representative |
Percent |
Fraction |
Reduced Fraction |
Decimal |
|
Example |
|
10% |
|
|
0.1 |
|
Example |
|
15% |
|
|
0.15 |
|
SC 1. |
|
45% |
|||
|
SC 2. |
|
|
|||
|
SC 3. |
|
1.5 |
 Self-Check
Self-Check
Are you ready for some more practice? Try these questions to build your skills!
SC 4. Write ![]() as a decimal and a percent.
as a decimal and a percent.
SC 5. Write 30% as a decimal and a fraction.
SC 6. Write 2.5 as a fraction and a percent.
Decimal and Percent Shortcut
Did you notice the shortcut between decimals and percent?
What is 35% as a decimal?
What is 0.20 as a percent?
1.8. Page 3
Module 8: Daily Living
Explore
Discounts
Which is the better sale: 25% off or $10.00 off? The answer will depend on the original cost of the item. But how can you figure out how much money you will save when you are just given a sale discount as a percentage? This next example will show you how to change a percent discount into actual dollar-and-cents savings.

Socks are on sale for 25% off. How much money would you save in this sale?
Example 1
Brandon is looking at a menswear flyer. Dress socks regularly priced at $7.99 a pair are advertised at 25% off.
- What is the discount?
- What is the discounted price?
Solution

25% = 0.25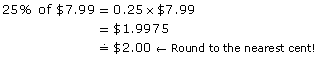
The discount is $2.00.
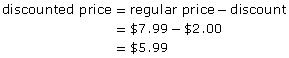
 Try This
Try This
discount: price reduction as a percent or a dollar value
In this activity you will calculate sales prices from percent discounts advertised in flyers or on the Internet. You will need a few sales flyers or access to your favourite retailer on the Internet.
Step 1: Select a flyer you received or go to the website of your favourite retailer. Look for at least five items that are reduced by a percent discount. Calculate the dollar discount and the discounted price, as in Example 1.
Remember to save your work in your course folder; your teacher may ask to see your work.
TT 1. Complete a table like the following. Round calculated prices to the nearest cent.
|
Item Description |
Regular Price |
Percent Discount |
Discount |
Discounted Price |
|
dress socks (1 pair) |
$7.99 |
25% |
$2.00 |
$5.99 |
|
a.
|
||||
|
b.
|
||||
|
c.
|
||||
|
d.
|
||||
|
e.
|
TT 2. Is there a way to determine the discounted price without first finding the dollar discount? If there is, show how this is done using your five examples.
TT 3. Search the Internet for a percent calculator, which may help in checking your table entries. There are a number available for both the computer and cellphone. Find at least three such calculators, and rank the calculators according to suitability and ease of use. You might even find yourself using the best calculator you find in the future to guide your own shopping!
 Share
Share
Share the percent calculators you found with other students. Compare the different calculators found and decide amongst yourselves which calculator is the best. What criteria did the group use to decide on the best percent calculator? Save and use this percent calculator during the rest of this lesson and module to check your work.
1.9. Page 4
Module 8: Daily Living
Bringing Ideas Together
In Explore, you examined price discounts (in percent, %, and in dollar amount, $). In Example 2 you will look at an alternate method you could use to answer the same questions you’ve already answered in this lesson. Maybe you will find this method suits you better.
Example 2
The regular price of a child’s toy guitar is $16.00. The guitar is on sale for 25% off. What is the discounted price?
Solution: Alternate Method
Determine the discounted price by subtracting the percent discount from 100. If the original price is discounted 25%, the discounted price must be 100% - 25% = 75% of the original price. If you look at the status bar image, the area not filled in with red is equal to the discounted price, 75%.
![]()
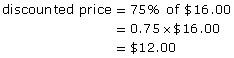
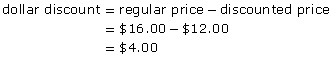
 Self-Check
Self-Check
In the following question you will use the two methods shown in Examples 1 and 2 to find the discounted price.
SC 7. A 32” LCD television is regularly $399.99. This week the store is offering a 5% discount. What is the dollar discount and the discounted price? Use both methods shown in Examples 1 and 2.
Price Increases
selling price: the price to be paid by the customer
selling price = wholesale price + mark-up
wholesale price: cost of an item purchased from a wholesale outlet
mark-up: the amount, as a percent or dollar value, by which a store increases the price of an item
The same approach used to find price discounts can be used to find price increases. When would finding percent increases be helpful? Stores, for example, purchase goods from wholesalers for less than the selling price—the price they sell the same goods to customers for. Stores need to add a mark-up to the wholesale price to cover costs, such as salaries, rent, and utility bills.
How much do you think the grocery store paid for the pack of gum you bought for $1.99 last week? You might think of the selling price as the wholesale price plus the mark-up.
Example 3
The local electronics store buys a certain brand of digital camera for $75.00 and marks the price up 70%. What is the dollar mark-up and what is the selling price?
Solution
![]()
Method 1
First, find the dollar mark-up.
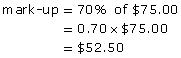
Then find the selling price.
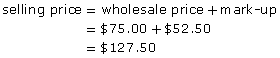
Method 2
Find the selling price first.
The wholesale price was increased by 70%. So, the selling price is
![]()
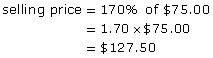
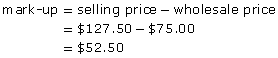
 Self-Check
Self-Check
In the following questions you will use both methods to find the increased prices.
SC 8. The neighbourhood florist has purchased specialty vases for $9.00 apiece wholesale. The florist intends to mark up the vases by 75%. What are the dollar mark-up and the selling price? Use both methods as shown in Example 3.
SC 9. Taxes are another way prices are increased. When you purchase most things in Canada, you will have to pay an additional 5% goods and services tax (GST). Many provinces also have a sales tax. Both tax calculations are based on the original purchase price.
In 2010, in Manitoba, the provincial sales tax is 7% and the federal GST is 5%. Fabbio has just purchased a slow cooker listed at $17.99 from a store in Winnipeg. What was the total cost of his purchase? How much did he pay in taxes?
1.10. Page 5
Module 8: Daily Living
Dollar Discounts into Percent Discounts
Often in a sales flyer, the discount is quoted in dollar value rather than as a percent. In the next part of the lesson, you will convert dollar discounts to percent discounts.
Example 4

© nexusseven/12086745/Fotolia
Dual shock controllers for gaming are $49.99 after a discount of $5.00. What was the original price and what is the percent discount? Round to the nearest tenth of a percent.
Solution
![]()
You must determine what a $5.00 discount on an original price of $54.99 is as a percent, or out of 100. Let the percent discount be x%.
Method 1
Set up a proportion.
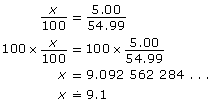
The discount is approximately 9.1%.
Method 2
Divide the dollar discount by the original price. Then convert to a percent.
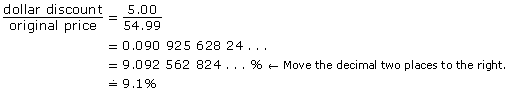
The discount is approximately 9.1%.
Example 5
A clothing store buys a line of men’s suits for $150.00 each from a suit wholesaler. The store owner decides he must mark up the price of each suit by $90.00 in order to make a profit. What is the percent mark-up?
Solution
View the animated “Example 5 Solution: Percent Mark-up Solution.”
 Self-Check
Self-Check
SC 10. A business-supply store advertises anti-virus software for $29.99. This price is after a $30.00 discount.
- What was the original price of the software?
- What is the percent discount? Round your answer to the nearest tenth of a percent.
SC 11. A portable GPS is advertised for $119.96. This price is after a $30.00 discount.

map and GPS: © Stephen VanHorn/4144634/Fotolia
- What was the original price of the GPS?
- What is the percent discount? Round your answer to the nearest tenth of a percent.
SC 12. A cellphone store purchases a popular cellphone for $40.00 wholesale. The store sells the phone for $69.99.
- What is the dollar mark-up?
- What is the percent mark-up? Round to the nearest tenth of one percent.
 Mastering Concepts
Mastering Concepts
Macey runs a gift store in Whitehorse. She has purchased stone inukshuk souvenirs at a wholesale price of $40.00 each.
- At the beginning of July, Macey marked up the wholesale price by 60%. There are a few inukshuk souvenirs left near the end of the summer. Macey discounts the selling price 25% for her annual clearance sale. What is the discounted price?
- Suppose Macey had bought the inukshuks when the wholesaler was having a sale. Assume the discount on the wholesale price was 25%, and then Macey marked up the discounted price by 60%. What would the selling price have been?
- Compare the calculations and the answers for parts a and b. What can you conclude about the order of percent increases and decreases and their effect on the final price.
1.11. Page 6
Module 8: Daily Living
Lesson Summary

© diego cervo/7895251/Fotolia
If you are interested in a career in retail, one of the mathematical skills you will need is working with percent. You will need to determine appropriate selling prices by calculating the mark-up required to pay for business expenses and provide for profits. During sales, you will have to calculate discounts.
In this lesson you explored this question:
How are percentages used to calculate discounts, mark-ups, and sales taxes?
Check your level of understanding of the materials covered in this lesson by completing “Lesson 2 Traffic Lights.” If you select an amber or red traffic light in the multimedia piece, you will receive information about additional work you can complete to improve your understanding of the topics.
Complete the suggested work before you proceed to the Lesson 2 Assignment. If you experience difficulty, contact your teacher before starting the Lesson 2 Assignment.
In this lesson you analyzed selling prices after applying either a dollar or percent increase or decrease.
 Assignment
Assignment
Retrieve the Lesson 2 Assignment Booklet you saved in your course folder at the start of this lesson. Complete the Assignment Booklet.
Resave your Assignment Booklet in your course folder and submit a copy to your teacher for assessment.
Unit 4 Project
Have you given some more thought to the Unit 4 Project? One of the possibilities is a career in sales or retail. In these areas, your ability to handle percents is a critical skill. For more information about this step and later steps of the task, review the Unit 4 Project.
1.12. Lesson 3
Module 8: Daily Living
Lesson 3: Currency Exchange
Focus

© Paul Maguire/2353825/Fotolia
During the spring break, Anna’s mother will be attending an Aboriginal Studies conference in the Florida Keys. Anna will be travelling with her! This is the first time Anna will be in the United States. Anna is very excited because they might even have time to go to Disney World and Universal Studios!
Anna and her mother have booked their trip through a local travel agent. The travel agent has been very helpful and has given them advice on what they will need, from passports to American currency. The travel agent has a map on the wall of some of the places she has visited, and Anna thinks to herself, “I bet being a travel agent would be a great career!”
Anna plans to change C$200.00 into American dollars at the bank. She wonders, “If I didn’t spend a cent of the American cash I take with me, would I get the full C$200.00 back if I exchanged it back to Canadian dollars after my trip?”
Lesson Questions
In this lesson you will explore these questions:
-
What are currency exchange rates?
-
What is the difference between the selling rate and the buying rate when exchanging currencies?
-
How are exchange rates used to convert between the Canadian dollar and foreign currencies?
Assessment
You will complete the Lesson 3 Assignment Booklet for assessment. Download the Lesson 3 Assignment Booklet and save it in your course folder now. You will receive instructions on how to complete the Assignment Booklet later in the lesson. You will also be prompted to continue working on the Unit 4 Project.
Remember to save all activities, including those that are not part of the Assignment Booklet, in your course folder.
Required Materials and Equipment
You will need your calculator, access to the Internet, and your problem-solving skills.
1.13. Page 2
Module 8: Daily Living
Get Started
currency: the money a country uses, such as the dollar in Canada, the pound in the United Kingdom, or the euro in the countries of the European Union
Have you purchased items over the Internet where prices were given in American dollars, British pounds, or even euros, which is the currency used by countries in the European Common Market? If you have, you know that you have to convert those currencies into Canadian dollars to estimate what the cost to you will actually be.
In the next activity you will search the Internet for particular items priced in foreign currencies. This activity will give you an idea of the relative values of these currencies.
Did You Know?
The largest bill ever printed in the United States was the 1934 gold certificate worth US$100 000.
 Self-Check
Self-Check

© Ratmandude/Dreamstime
Heather is saving towards buying her first car. She has her eye on a subcompact, fuel-efficient hatchback. She wonders whether she would pay more or less than she would in Canada if she were to buy the car in another country.
HEATHER’S RESEARCH
Canada |
C$14 750 |
Canadian dollars |
United States |
US$12 605 |
United States dollars |
United Kingdom |
£10 256 |
United Kingdom pounds |
France |
€12 190 |
European euros |
Russia |
RUB705 000 |
Russian rubles |
Work with a partner, if possible, to complete the following questions.
SC 1. Is there something you, like Heather, would like to buy? Look up that item on the Internet and find its price in Canada and in at least three other countries. Record the prices in the currency of each country.
SC 2. Is it possible to determine where the item would be the least expensive? Why or why not?
Currency Exchange Rates

© duckman76/18746052/Fotolia
In order to travel to or do business in other countries, you must be able to convert between the currency used in your country and the currency used in the other country. For example, if you travelled to Mexico on a winter vacation, you would need to bring Mexican pesos rather than Canadian dollars. Do you know how many Mexican pesos are equivalent to C$1.00?
On February 2, 2010, C$1.00 was equal to Mex$12.1271. So, Mex$1.00 was approximately 8¢. This is an example of a currency exchange rate.
currency exchange rate: the relative value of one currency to another
The date was given for the conversion between the Canadian dollar and the Mexican peso because exchange rates are always changing. Exchange rates depend on what business and investors are willing to pay. The relative value of the Canadian dollar will rise, for example, when there is a demand for Canadian dollars to pay for the goods Canada exports or to invest in Canada.
Conversions between currencies are handled by banks, investment houses, currency exchanges, and other financial institutions. If you were travelling to the United States, you could, for instance, go to the bank or to a currency exchange kiosk at an airport to buy American dollars.
1.14. Page 3
Module 8: Daily Living
Explore
For this activity you will need your calculator and access to the Internet.
 Try This
Try This
In this activity you will convert foreign currency amounts into Canadian dollars using an online currency converter.
The Bank of Canada website has a currency converter. You can find this currency converter by searching the Internet using the words Bank of Canada currency converter. You can use this converter to explore exchange rates among major currencies. These rates are updated daily. You can look up current rates, or you can explore rates for any date in the past ten years.
nominal exchange rate: an exchange rate that does not include transaction fees
In this activity, when working with the Bank of Canada currency converter, select the nominal exchange rate. The cash rate includes an estimate of the fees commercial banks and other financial institutions charge customers to convert their currency. These fees are to cover the cost of doing business, and they include a profit margin. The nominal rate does not include these transaction fees.
In the Bank of Canada currency converter, select the currency you wish to convert from the “From” list. Select the currency you wish to exchange into from the “To” list. For instance, if you were converting Canadian dollars into US dollars, you would select “Canadian dollar” in “From” and “US dollar” in “To.” Finally, enter the amount you wish to convert without spaces or any currency symbol, and then click “Convert.”
You will recall from the example in Get Started that Heather was interested in the prices (exclusive of taxes and other charges) consumers pay in several other countries for a particular subcompact, fuel-efficient hatchback she would love to own. Her research was as follows.
HEATHER’S RESEARCH
Canada |
C$14 750 |
Canadian dollars |
United States |
US$12 605 |
United States dollars |
United Kingdom |
£10 256 |
United Kingdom pounds |
France |
€12 190 |
European euros |
Russia |
RUB705 000 |
Russian rubles |
On February 3, 2010, Heather used the Bank of Canada website to convert the foreign amounts into Canadian dollars to see where the car was least expensive and where it was most expensive. Here are Heather’s results.
HEATHER’S RESEARCH IN CANADIAN DOLLARS
Subcompact Hatchback |
Price in Foreign Currency |
Price in |
Canada |
$14 750.00 |
|
United States |
US$12 605 |
$13 372.64 |
United Kingdom |
£10 256 |
$17 315.20 |
France |
€12 190 |
$17 983.91 |
Russia |
RUB705 000 |
$24 935.85 |
It appears the hatchback is least expensive to buy in the United States and most expensive in Russia. The prices in the United Kingdom and in France are similar.
TT 1. Set up a table like “Heather’s Research in Canadian Dollars.” Use the Bank of Canada’s currency converter for today’s date to complete the last column of the table. How do your results differ from Heather’s results? Why do you think that is?
TT 2. You will recall that, in Get Started, you looked up foreign prices for an item in which you were interested. Set up a table for your item, just like Heather did for the hatchback. Use the Bank of Canada currency converter set to today’s date. Based on Canadian dollars, where is your item the most expensive? Where is your item the least expensive?
TT 3. The Bank of Canada’s currency converter isn’t the only currency converter on the Internet. Search for at least three other currency converters. You may wish to look for an application you can download to your cellphone. Rank the calculators you find for accuracy and ease of use. Be prepared to share your results with other students.
 Share
Share
Share your answers to TT 1 to TT3. Use the discussion area for your class or another method indicated by your teacher to post your answers and to view the work of the people you are sharing with. Compare your answers. Identify where you have similar answers and where your answers are different.
View the applications other students downloaded to their cellphones. Which application is the best? Would such a currency converter be useful to you?
1.15. Page 4
Module 8: Daily Living
Bringing Ideas Together
In Explore you compared prices in foreign currencies to prices in Canadian dollars. The Bank of Canada currency converter is an efficient tool for making these comparisons. However, you may not always have access to an online currency converter. Nominal exchange rates are printed in the business or financial sections of most large, daily newspapers.
The following table was compiled from rates available on February 3, 2010. In this table foreign currencies are compared to the Canadian dollar. Most tables are much more extensive and list many more currencies!
|
Currency Unit |
Units per C$1.00 |
Number of CAD per Unit |
|
|
ARS |
Argentina Pesos |
3.611 723 702 8 |
0.276 876 107 4 |
|
AUD |
Australia Dollars |
1.068 204 878 2 |
0.936 150 003 0 |
|
BMD |
Bermuda Dollars |
0.941 902 107 9 |
1.061 681 454 6 |
|
BRL |
Brazil Reals |
1.748 147 656 1 |
0.572 034 059 3 |
|
CAD |
Canada Dollars |
1.000 000 000 0 |
1.000 000 000 0 |
|
CLP |
Chile Pesos |
506.978 809 574 3 |
0.001 972 469 0 |
|
CNY |
China Yuan Renminbi |
6.431 307 657 4 |
0.155 489 373 7 |
|
COP |
Colombia Pesos |
1846.068 238 870 6 |
0.000 541 691 8 |
|
CRC |
Costa Rica Colones |
520.400 914 611 7 |
0.001 921 595 4 |
|
DKK |
Denmark Kroner |
5.047 264 950 1 |
0.198 127 106 4 |
|
DOP |
Dominican Republic Pesos |
34.049 761 200 4 |
0.029 368 781 6 |
|
EGP |
Egypt Pounds |
5.139 017 760 5 |
0.194 589 714 7 |
|
EUR |
Euro |
0.677 984 660 5 |
1.474 959 624 2 |
|
HKD |
Hong Kong Dollars |
7.315 705 823 9 |
0.136 692 210 4 |
|
ISK |
Iceland Kronur |
119.859 046 614 0 |
0.008 343 133 3 |
|
INR |
India Rupees |
43.431 106 769 9 |
0.023 024 971 6 |
|
ILS |
Israel New Shekels |
3.491 919 786 3 |
0.286 375 421 3 |
|
JMD |
Jamaica Dollars |
84.042 384 042 5 |
0.011 898 758 1 |
|
JPY |
Japan Yen |
85.767 463 970 6 |
0.011 659 433 0 |
|
JOD |
Jordan Dinars |
0.667 808 586 4 |
1.497 435 074 0 |
|
KES |
Kenya Shillings |
71.537 462 220 1 |
0.013 978 689 9 |
|
LBP |
Lebanon Pounds |
1415.207 917 111 6 |
0.000 706 610 0 |
|
MYR |
Malaysia Ringgits |
3.218 479 502 7 |
0.310 705 722 7 |
|
MXN |
Mexico Pesos |
12.218 467 481 6 |
0.081 843 324 6 |
|
NZD |
New Zealand Dollars |
1.331 680 148 6 |
0.750 931 070 8 |
|
NOK |
Norway Kroner |
5.534 052 405 6 |
0.180 699 409 2 |
|
PKR |
Pakistan Rupees |
80.009 364 073 7 |
0.012 498 537 0 |
|
PEN |
Peru Nuevos Soles |
2.686 915 693 1 |
0.372 173 940 0 |
|
PHP |
Philippines Pesos |
43.258 179 492 0 |
0.023 117 015 4 |
|
PLN |
Poland Zlotych |
2.720 219 260 4 |
0.367 617 425 0 |
|
RUB |
Russia Roubles |
28.142 067 014 8 |
0.035 533 992 6 |
|
SAR |
Saudi Arabia Riyals |
3.532 198 542 8 |
0.283 109 793 5 |
|
ZAR |
South Africa Rand |
7.078 298 970 2 |
0.141 276 880 8 |
|
SEK |
Sweden Kronor |
6.859 767 248 5 |
0.145 777 540 8 |
|
CHF |
Switzerland Francs |
0.997 856 390 0 |
1.002 148 215 0 |
|
THB |
Thailand Baht |
31.162 830 375 4 |
0.032 089 511 4 |
|
TRY |
Turkey Lira |
1.407 776 526 2 |
0.710 340 015 9 |
|
GBP |
United Kingdom Pounds |
0.592 765 854 6 |
1.687 006 753 5 |
|
USD |
United States Dollars |
0.941 902 107 9 |
1.061 681 454 6 |
|
VEF |
Venezuela Bolivares Fuertes |
4.050 179 063 9 |
0.246 902 663 9 |
Take a look at Example 1 to see how the table is used.
Example 1
As part of a school tour, Eddy and several of his classmates are travelling in France. They have just stopped to eat in a small cafe. The luncheon special costs €12.00.
- How might Eddy and his friends use their knowledge about the relative value of the Canadian dollar and the euro to estimate the cost of the special in Canadian dollars?
- Use the table to determine the cost of the luncheon special in Canadian dollars. Round to the nearest cent.
Solution
€ → C$
|
Units per C$1.00 |
Number of CAD per Unit |
||
|
EUR |
euro |
0.677 984 660 5 |
1.474 959 624 2 |
From the table C$1.00 = €0.677 984 660 5, and €1.00 = C$1.474 959 624 2.
- Eddy and his friends know that €1.00 is approximately C$1.50. “I know,” says Eddy. “$1.50 is 1
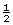 dollars. So take
dollars. So take 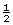 of 12. That’s 6. Add 6 to 12. That will be 1
of 12. That’s 6. Add 6 to 12. That will be 1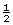 times. That’s 18. The special will cost about C$18.00.”
times. That’s 18. The special will cost about C$18.00.”
Eddy’s friend takes out a pen and multiplies 12 by 1.5. 12 × 1.5 = 18!
- Since you want to convert euros to dollars, use €1.00 = C$1.474 959 624 2.
€1.00 = C$1.474 959 624 2
€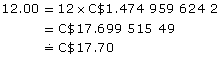
The special costs C$17.70.
Example 2
Carl has a cousin in England who is a plumbing and heating installation and repair technician. Last year, Carl’s cousin earned £32 000. Carl has a similar job in Canada and earned $54 000. Compare their earnings.
Solution
|
Currency Unit |
Per C$1.00 |
Number of CAD per Unit |
|
GBP (United Kingdom Pounds) |
0.592 765 854 6 |
1.687 006 753 5 |
£→C$
|
Method 1 |
Method 2 |
|
|
|
Carl earned C$54 000.00 - C$53 984.22 = C$15.78 more than his cousin last year.
View the animated “Example 2 Solution: Currency Conversion.”
Try the following questions based on the currency-exchange table.
 Self-Check
Self-Check
SC 3. Janice is holidaying in Mexico. She sees a silver bracelet in a gift shop for Mex$800.00.
- How might Janice estimate the cost in Canadian dollars?
- Use the table to determine the cost in Canadian dollars to the nearest cent.
SC 4. On an online shopping website, a composite goalie stick is advertised for US$65.00. Excluding transaction fees, taxes, and shipping, what is the price in Canadian dollars?
SC 5. Hera has just opened a US-dollar investment account. She wishes to invest C$12 450.00. What is that sum in US dollars?
SC 6. Why are there so many decimal places given in currency-exchange tables?
1.16. Page 5
Module 8: Daily Living
Using Conversion Factors
If you look at the foreign-exchange table, you will notice that both the conversion factors for changing Canadian dollars into a foreign currency and the conversion factor for changing a foreign currency into Canadian dollars are given. This is very convenient. If you were converting between Chinese Yuan and Canadian dollars, you would simply refer to the following line in the table.
|
Units per C$1.00 |
Number of CAD per Unit |
||
|
CNY |
China Yuan Renminbi |
6.431 307 657 4 |
0.155 489 373 7 |
To convert C$100.00 to Chinese Yuan, you would use the first conversion factor and multiply.
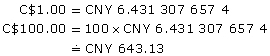
To convert CNY 100.00 to Canadian dollars, you would use the second conversion factor and multiply.
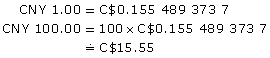
However, what would you do if you only knew one conversion factor? This is where knowing how to set up proportions becomes very useful.
Study the following example.
Example 3
Marcel is reviewing his financial records. On January 22, 2003, he transferred C$500.00 into a US-dollar savings account. If, on that date, US$1.00 = C$1.532, what was Marcel’s deposit in US dollars? Disregard fees and commissions.
Solution
Method 1
Set up a proportion. Let x be the deposit in US dollars. On the other side of the equal sign is the conversion rate. The numerators of the ratios in the proportion must be in one currency, and the denominators in the other currency. Since the unknown is in US dollars, it may be preferable to put US dollars on top, since this creates fewer steps to solve and no cross-multiplying is necessary.
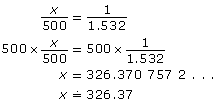
On January 22, 2003, Marcel deposited US$326.37.
Method 2
Divide by the conversion factor. Since US$1.00 = C$1.532, if you were given a sum in American dollars, you would multiply by 1.532 to convert the sum into Canadian dollars. To reverse the process in order to change Canadian dollars into American dollars, you would divide.
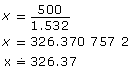
On January 22, 2003, Marcel deposited US$326.37.
 Self-Check
Self-Check
In each of the following questions, apply both methods shown in Example 3.

© Jgz/4678816/Fotolia
SC 7. On March 20, 2009, Victor was in Peru on his way to the Inca city of Machu Picchu. He was going to witness the sun on the Intihuatana stone at noon during the equinox. On March 20, he spent PEN 450.00. That day, C$1.00 was equal to PEN 2.5189. What did Victor spend in Canadian dollars?
SC 8. On October 1, 2009, the Cardinal family stayed at a motel in Sydney, Australia. The charge for the room was A$150.00. If on that date, C$1.00 was equal to A$1.0632, what was the room charge in Canadian dollars?
Buy and Sell Exchange Rates
Up to this point in the lesson you have worked with nominal currency exchange rates. There were no transaction fees. However, nothing in life is free. Banks and other financial institutions charge a percentage of the currency exchange as their commission. This commission is often 4%.
These fees may vary depending on whether the transaction is in cash, involves a cheque, is a credit card transaction,
or is an investment. The fees also depend on the amount of the exchange, and the fees may be negotiable.
buy and sell exchange rates: exchange rates reflecting transaction fees
For customers wishing to exchange currency, banks will advertise their buy and sell exchange rates based on whether they are selling the foreign currency to the customer or buying the foreign currency from the customer. The exchange rates for selling and buying are different from one another, and they both differ from the nominal exchange rates because they include fees.
Consider the Royal Bank of Canada’s Buying and Selling Rates from February 3, 2010. You may wish to print this document.
Study the following examples to see the effects of built-in fees.
Example 4
Yolanda walks into the bank and asks to exchange C$100.00 for US dollars. The teller consults the “Sell to You” column, because the bank is selling US dollars to Yolanda. The rate is US$1.00 = C$1.0855.
- What will the amount be in US dollars?
- If Yolanda changes her mind shortly afterwards, and returns to the bank to exchange the US dollars back into Canadian dollars, the teller will consult the “Buy from You” column. The rate is US$1.00 = C$1.0303. How much money will Yolanda receive in Canadian dollars?
- What were the total fees for the two transactions?
Solution
- Let x be the amount in US dollars. Since US$1.00 = C$1.0855, you will end up with less than US$100.00. Divide C$100.00 by the conversion rate.
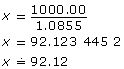
Yolanda will receive US$92.12 for her C$100.00.
- US$1.00 = C$1.0303
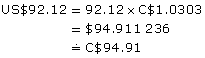
Yolanda receives C$94.91.
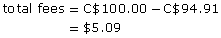
 Self-Check
Self-Check
Use the Royal Bank of Canada’s Buying and Selling Rates from February 3, 2010, to answer these questions.
SC 9. Xena has been on a holiday in Germany. On her return to Canada, she has €350.12 in cash. She exchanges the euros for Canadian dollars. How much does she receive in Canadian money?
SC 10. Wilma is planning a trip to Sweden. She goes to the bank to exchange C$500.00 for Swedish Kronas. How much will she receive in Swedish Kronas?
SC 11. Quincy has turned 17. He received a cheque for £50.00 from his uncle in Scotland. How much will Quincy receive in Canadian dollars from the bank?
 Mastering Concepts
Mastering Concepts
On Thursday, the exchange rate for the Australian dollar was C$1.00 = A$1.0692. On the same day, the exchange rate for the euro was C$1.00 = €0.6678. Complete the following conversions. Round to four decimal places.
- €1.00 = A$?
- A1.00 = €?
1.17. Page 6
Module 8: Daily Living
Lesson Summary
© Stasys Eidiejus/8101755/Fotolia
In this lesson you explored the following questions:
What are currency exchange rates?
-
What is the difference between the selling rate and the buying rate when exchanging currencies?
-
How are exchange rates used to convert between the Canadian dollar and foreign currencies?
Check your level of understanding of the materials covered in this lesson by completing “Lesson 3 Traffic Lights.” If you select an amber or red traffic light in the multimedia piece, you will receive information about additional work you can complete to improve your understanding of the topics. Complete the suggested work before you proceed to the Lesson 3 Assignment. If you experience difficulty, contact your teacher before starting the Lesson 3 Assignment.
In Lesson 3 you examined nominal currency exchange rates and exchange rates reflecting transaction fees charged by financial institutions, such as banks and credit unions. You used various tools to solve problems involving these rates. These tools included online currency converters, tables, proportional reasoning, and conversion factors.
 Assignment
Assignment
Retrieve the Lesson 3 Assignment Booklet you saved in your course folder at the start of this lesson. Complete the Assignment Booklet.
Resave your Assignment Booklet in your course folder and submit a copy to your teacher for assessment.
Unit 4 Project
Have you given some more thought to the Unit 4 Project? Does the career or job you would like to explore involve handling foreign currencies? If so, have you thought of some questions related to currency exchange you will ask during your interview with the person in that career or job? For more information about this step and later steps of the task, review the Unit 4 Project.
1.18. Lesson 4
Module 8: Daily Living
Lesson 4: Being Paid on the Job: Salaries and Wages
Focus

© Okea/19024359/Fotolia
Randy is a welder. After completing Grade 12, he enrolled in a welding program at the Northern Alberta Institute of Technology. He successfully completed the coursework and a three-year apprenticeship.
Randy now works in the Edmonton area. From time to time, he also works in Fort McMurray. He does not work for a single empoyer. Instead, Randy works for several employers at various job sites. Randy obtains these jobs though his union. Right now he is on a job at a large refinery.
At his current job, Randy’s wage is $35.00/h for an eight-hour shift. Randy is paid time-and-a-half in overtime if his shift is longer than eight hours. On Friday, Randy worked a ten-hour shift. How much extra money did Randy make for working a longer shift?
Did You Know?
In Fort McMurray, in 2009, the average rent for a two-bedroom unit was $2360/mo—the highest in Canada.
Lesson Questions
In this lesson you will explore these questions:
What are wages and salaries, and what are the jobs that commonly involve these ways of earning income?
What are the advantages and disadvantages of wages and salaries?
How is gross pay calculated from regular and overtime rates of pay?
Assessment
You will complete the Lesson 4 Assignment Booklet for assessment. Download the Lesson 4 Assignment Booklet and save it in your course folder now. You will receive instructions on how to complete the Assignment Booklet later in the lesson. You will also be prompted to continue working on the Unit 4 Project.
Remember to save all activities, including those that are not part of the Assignment Booklet, in your course folder.
Required Materials and Equipment
You will need your calculator, access to the Internet, and your inquiry skills.
1.19. Page 2
Module 8: Daily Living
Get Started
If you still aren’t sure which career path is best for you, or even if you have narrowed your career search to several possible occupations, now is the time to gather more information. Territorial and provincial agencies maintain excellent websites to help you explore occupations that reflect your skills and interests. In this activity you will assess careers and jobs through these websites.
 Try This
Try This
Begin by browsing the Career Planner set up by the Government of Alberta. To get to the Career Planner, you will need to enter the following keywords in an Internet search engine: career planner Government of Alberta. The Career Planner provides advice and information on the following areas:
career planning
specifics on hundreds of occupations
educational requirements
how to find a job
wage: the amount of pay a worker receives hourly or daily
The Career Planner also provides current wages and salary levels for occupations. For example, the 2009 wages and salary levels were compiled from over 344 000 individuals in over 450 occupations.
Research careers and job opportunities in Alberta and other parts of Canada. Use search terms such as Alberta Occupational Profiles, British Columbia Occupational Profiles, and so on.
Add any websites you come across to your course folder.
average (mean) wage: the wage determined by adding together the wages of every person surveyed and then dividing the total by the number of people surveyed
median wage: the wage determined by splitting people surveyed into two groups of equal numbers based on wage
The half earning more money will be above the median, and the half earning less money will be below the median.
When looking up wage and salary information, there are two terms you must know: average wage and median wage.
Example 1
Six people were asked to indicate how much they earned as an hourly wage. The results were as follows:
$18.00, $16.00, $17.00, $19.00, $65.00, and $21.00
- What is the median wage?
- What is the average wage?
Solution
- To find the median wage, you need to find the wage that is “in the middle.”
Order the wages from lowest to highest.
$16.00, $17.00, $18.00, $19.00, $21.00, $65.00
Highlight or circle the middle number. Since there is an even number of wages, highlight or circle the two middle numbers.
$16.00, $17.00, $18.00, $19.00, $21.00, $65.00
The median wage is $18.50, since that value is halfway (in the middle) between $18.00 and $19.00. Three people earn less than $18.50. Three people earn more than $18.50.
- To find the average wage, add up all the wages, and then divide by the total number of wages added together.
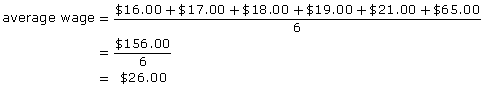
 Self-Check
Self-Check
Try the following questions based on information on the Government of Alberta’s Career Planner, which you explored earlier in this lesson.
SC 1. In Alberta, what is the average starting wage for a painter? What is the median starting wage?
SC 2. Why do you think there is a difference between the average wage and the median wage you identified in SC 1?
SC 3. Complete a table like the following based on Alberta wages.
|
Occupation |
Average Starting Hourly Wage |
Overall Hourly Wage |
|
Gas Fitter |
|
|
|
Nurse Aide |
|
|
|
Security Guard |
|
|
1.20. Page 3
Module 8: Daily Living
Explore
For this activity you will need access to the Internet. You will be exploring and gathering information online about specific occupations.
 Try This
Try This
Work with a partner, if possible.
To answer the following career-specific questions, you will need to access career websites, such as the ones you found in Get Started. If possible, explore websites in the territory or province in which you wish to work.

© Szasz-Fabian Erika/5966227/Fotolia
TT 1. Jolene is interested in becoming a hairstylist. What are the personal characteristics required for those entering this occupation?
TT 2. What are the typical duties of a hairstylist?
TT 3. What are the working conditions?
TT 4. What are the average earnings of a hairstylist? What earnings can you expect at the start? What are the possibilities for advancement?
TT 5. What are the educational requirements?
TT 6. Select an occupation in which you are interested. Answer questions TT 2 to TT 5 again for this occupation.
 Share
Share
Share the information you found for TT 6. Explore the occupation information of other students. Has anyone else chosen a similar occupation? How do their findings compare to yours? Did anyone choose an occupation that is new to you? Did any of the wages or educational requirements surprise you? Take some time to view the research of others before moving on in the lesson.
Save a copy of your response to TT 6 in your course folder.
1.21. Page 4
Module 8: Daily Living
Bringing Ideas Together
In Get Started and Explore, you examined several occupations and what you could expect in wages.
minimum wage: the least wage a worker can be paid
Minimum wage is generally given in dollars per hour.
Construction workers, factory workers, fast-food workers, grocery clerks, and cashiers are just a few of the many employees that are paid a wage for their labour. In Canada, there are laws governing minimum wages.
Minimum wages are set by government legislation. In Alberta, as of February 2010, the minimum hourly wage was $8.80/h.
As of February 1, 2010, for adult workers, the following minimum wages were in effect.
|
Province/Territory |
Minimum Hourly Wage |
|
Alberta |
$8.80 |
|
British Columbia |
$8.00 |
|
Manitoba |
$9.00 |
|
Northwest Territories |
$8.25 |
|
Nunavut |
$10.00 |
|
Saskatchewan |
$9.25 |
|
Yukon Territory |
$8.89 |
You read about a welder named Randy in Focus. Now listen to Randy discuss his wages in “Overtime.”
overtime wages: wages for working beyond a certain number of hours
At the least, wages for working overtime are 1![]() times the regular rate. This may differ depending on work agreements.
times the regular rate. This may differ depending on work agreements.
Depending on your salary agreement, your situation may differ from the standards Randy described, and you may receive overtime wages for fewer hours worked. Also, if you live in another province, the rules will be different.
Study these examples.
Example 2
Jerry works at a greenhouse near Edmonton. He is paid minimum wage. One week in 2010, he worked 50 h. His employer pays overtime after 44 h. If the overtime rate is 1![]() times his regular wage, what were Jerry’s total earnings for the week?
times his regular wage, what were Jerry’s total earnings for the week?
Solution
The minimum wage in Alberta, in 2010, is $8.80.
![]()
Jerry worked 50 h. He was paid for 44 h at the regular rate and for 6 h at the overtime rate.
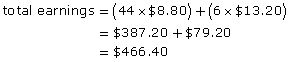
Jerry’s total earnings were $466.40 for that week.
Example 3
Sanjit was hired to work part-time at $10.00/h. His job is to stock shelves in a new supermarket in Fort St. John, British Columbia. On Tuesday, Sanjit worked 14 h. In British Columbia, workers are paid time-and-a-half (1.5 × regular hourly pay) for overtime after 8 h, and double-time (2 × regular hourly pay) for overtime after 12 h.
How much did Sanjit earn on Tuesday?
View “Example 3 Solution: Wages Solution.”
Gross Pay
gross pay: the total earned, before deductions, in a pay period
time sheet: a record of an employee’s time at work
In Example 2 and Example 3, you calculated gross pay.
A company will determine wages (both regular and overtime) from the employees’ time sheets.
Example 4
Linda works on the grounds crew of a local golf course. Her regular pay is $10.50/h. She is paid overtime at 1![]() the regular rate on any day she works over 8 h or if she works over 44 h/wk. The payroll clerk calculates her gross pay from her weekly time sheet. Time in hours and minutes spent on the job is converted to hours rounded to two decimal places.
the regular rate on any day she works over 8 h or if she works over 44 h/wk. The payroll clerk calculates her gross pay from her weekly time sheet. Time in hours and minutes spent on the job is converted to hours rounded to two decimal places.
- On a Monday last August, Linda worked 9 h 15 min. What is her time in hours?
- Calculate Linda’s gross pay for the Monday.
View “Example 4 Solution: Linda’s Gross Pay.”
Example 5
During the summer Edgar works for a landscape company. He receives $12.00/h for regular hours. He is paid time-and-a-half if he works over 8 h a day or 44 h/wk. The following was Edgar’s time sheet for a week last September.
|
Employee: Edgar Strawberry |
Mon. |
Tues. |
Wed. |
Thurs. |
Fri. |
Totals |
|
Regular Hours |
8.00 |
8.00 |
4.00 |
7.00 |
9.25 |
36.25 |
|
Overtime Hours |
|
2.50 |
|
|
|
2.50 |
- There is an error in Edgar’s time sheet. What is the error? Correct the time sheet.
- Use the corrected time sheet from part a to determine Edgar’s gross pay for the week.
Solution
- There is a mistake in the Friday hours. Edgar should be paid at the overtime rate for time over 8 h.
Employee:
Edgar Strawberry
Mon.
Tues.
Wed.
Thurs.
Fri.
Totals
Regular Hours
8.00
8.00
4.00
7.00
8.00
35.00
Overtime Hours
2.50
1.25 3.75
- regular rate = $12.00/h
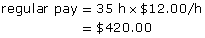
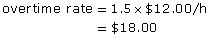
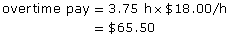
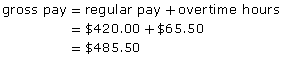
 Self-Check
Self-Check
SC 4. Bryce works in a warehouse. He “punches” a time card when he starts work and when he leaves work. He also swipes his time card when he leaves and returns for lunch.
BRYCE BERNIER
|
Tuesday, January 15, 2011
|
Time In
|
Time Out
|
|
AM |
8:05 |
|
|
|
12:07 |
|
PM |
1:17 |
|
|
|
6:02 |
- How long did Bryce work on Tuesday? (Remember there are 60 min in 1 h.)
- What was Bryce’s total time in hours, rounded to two decimal places?
- Bryce’s regular pay is $14.25/h. He earns double-time pay (2 × regular pay) for overtime if he works longer than 8 h. How much did Bryce earn on Tuesday?
SC 5. Lisa works as a mechanic at Carmen Motors. Her regular wage is $25.00/h. She earns double-time pay after 8 h. On Wednesday, Lisa’s gross earnings were $275.00. How long did Lisa work on Wednesday?
SC 6. Harry is paid $14.00/h as a labourer. He is paid time-and-a-half after 8 h on any given day or when he works more than 44 h in the week. Last week, he checked his time sheet.
|
Employee: Harry Holmes |
Mon. |
Tues. |
Wed. |
Thurs. |
Fri. |
Sat. |
Totals |
|
Regular Hours |
8.00 |
8.00 |
7.75 |
7.50 |
8.00 |
8:00 |
43.25 |
|
Overtime Hours |
|
|
|
|
|
|
0.00 |
Check to see if Harry’s time sheet is correct. If there are errors, correct them. Then calculate his gross pay for the week.
1.22. Page 5
Module 8: Daily Living
Shift Differential
Workers on wages may be paid extra for working Sundays or holidays. Depending on the working agreement, in some instances the wage could be paid at double-time, or the worker could receive time off in the future as compensation—time in lieu.
shift differential: a bonus paid to compensate workers taking an undesirable shift
In shift work, there may be bonuses paid to work the less-desirable shifts. For instance, a worker might be paid a 20% bonus for working the night shift. This bonus is called a shift differential.
Example 5
Morris works at a convenience store. On a regular shift, he is paid $12.00/h. When he works the night shift, he is paid a shift differential of 20%. What are his hourly wages on the night shift?
Solution
Method 1
Morris’s regular wages are $12.00/h. The night-shift bonus is 20%. So the hourly rate at night will be 100% + 20% = 120% of his regular wage.
120% = 1.20
120% of $12.00 = $14.40
$12.00 × 1.2 = $14.40
Morris’s wage at night is $14.40/h.
Method 2
Find the shift differential in dollars per hour. The bonus is 20%.
![]()
Morris receives an extra $2.40/h at night.
![]()
 Self-Check
Self-Check
In the next question you will calculate the shift differential as a percent.
SC 7. Anuka’s wage when he works the day shift is $15.00/h. When he works the evening shift, he earns $15.60/h. What is the shift differential as a percent?
Salaries
salary: a set amount paid to an employee for the performance of regular duties of a position over a period of one year (or other specified period of time)
To this point in Lesson 4, you have explored wages. Some employees, such as most clerical workers, managers, accountants, bankers, teachers, firefighters, clergy, and police officers, are not paid wages. Instead, these employees earn salaries.
An electrical engineer, for example, might sign a contract to work for a firm for an annual salary of $84 000. Of course, she would not be paid a lump sum; she would be paid monthly. Her monthly salary would $84 000 ÷ 12 months, or $7000 every month.
Did You Know?
In 2007, the average annual income for a family with two working parents was $77 300.
Employers prefer to pay their management, clerical, and professional staff salaries, as they know what the cost of each employee will be over the year. This is not the case with workers on wages; for wage employees, time on the job and overtime are difficult to predict.
Salaried employees often receive benefits, contribute to pension funds, and take fixed-length holidays that are not always available to workers on wages. And, unlike hourly workers, salaried workers generally do not have to punch a time clock. Unlike workers on wages, salaried employees know exactly how much they are going to earn each month, so it is easier for them to budget.
Salaried workers are not paid overtime for performing their regular duties. For example, school teachers, who are on a salary, are not paid overtime for planning and marking exams and assignments. Although this work may have to be done outside of standard work hours, it is simply considered part of the job.
Example 6
Kathy works as a dietitian in Whitehorse. She is a salaried employee. Her salary before deductions is $7240.00/mo.
- What is Kathy’s annual salary?
- Kathy’s employer says she will receive a 4% raise in January. What will Kathy’s annual salary be after the raise?
Solution
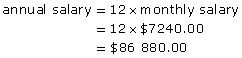
- With a 4% raise, Kathy will earn 100% + 4% = 104% of her present salary.
104% = 1.04
1.04 × $86 880.00 = $90 355.20
So, 104% of $86 880.00 is $90 355.20.
Next January, Kathy’s annual salary will be $90 355.20.
 Self-Check
Self-Check
In the next set of questions you will make decisions based on your knowledge of salaries and wages.
SC 8. Mary-Ellen is a plumber. She works for an hourly wage. Over the course of the year, she has worked for several different employers and at several different job sites. Last month, with regular wages and overtime, Mary-Ellen earned $6300.00. Can you predict Mary-Ellen’s annual income?
SC 9. Marty is an office-staff employee at the local Band Office. If his monthly salary is $4500.00, what is Marty’s annual salary?
When Does the Paycheque Arrive?
biweekly: every two weeks
semimonthly: twice a month
Businesses often pay their salaried workers monthly. However, some workers are paid biweekly or semimonthly.
For a worker who is paid biweekly, because there are 52 weeks in a year, there would be 52 ÷ 2, or 26, pay periods in the year.
For a worker who is paid semimonthly, because there are 12 months in a year, there would be 12 × 2, or 24, pay periods in the year.
You may have noticed that hourly wages are also unit rates ($/h). Salaries are also a unit rate ($/yr). With salaries, the unit could be changed and different unit rates calculated depending on whether the salary is paid biweekly ($/wk) or semimonthly ($/mo). The following Mastering Concepts question explores this concept.
 Mastering Concepts
Mastering Concepts
Jody has been hired as an office assistant at the local school. Her annual salary is $36 000.00. What would Jody’s salary be each pay period if she were paid as follows?
- monthly
- semimonthly
- biweekly
1.23. Page 6
Module 8: Daily Living
Lesson Summary

© Tootles/291654/Fotolia
In Lesson 4 you explored wages and salaries. Do you remember the differences between wages and salaries? Can you name at least three occupations that would earn a wage? A salary?
Look at the earnings statement in the man’s pocket. Do you think this individual is paid a wage or a salary? How would you justify your answer?
In this lesson you answered these questions
- What are wages and salaries, and what are the jobs that commonly involve these ways of earning income?
- What are the advantages and disadvantages of wages and salaries?
- How is gross pay calculated from regular and overtime rates of pay?
Check your level of understanding of the materials covered in this lesson by completing “Lesson 4 Traffic Lights.” If you select an amber or red traffic light in the multimedia piece, you will receive information about additional work you can complete to improve your understanding of the topics.Complete the suggested work before you proceed to the Lesson 4 Assignment. If you experience difficulty, contact your teacher before starting the Lesson 4 Assignment.
In Lesson 4 you examined occupations that involve payment by wages and salaries. Do you remember the advantages and disadvantages of each method of being paid? The primary focus of the lesson was wages. You used regular and overtime rates to determine gross pay from time sheets. You identified typical errors that might occur in time sheets, and you corrected those errors. You also explored shift differentials and how rates of pay for those shifts are calculated.
 Assignment
Assignment
Retrieve the Lesson 4 Assignment Booklet you saved in your course folder at the start of this lesson. Complete the Assignment Booklet.
Resave your Assignment Booklet in your course folder and submit a copy to your teacher for assessment.
Unit 4 Project
Have you given some more thought to the Unit 4 Project? Have you contacted an employee you can interview who works in the job or career you are planning to explore? Has this lesson helped you come up with questions you can ask about the job and how incomes are earned in that field? For more information about this step and later steps of the task, review the Unit 4 Project.
1.24. Lesson 5
Module 8: Daily Living
Lesson 5: Being Paid on the Job: Tips and Commissions
Focus

Photos.com/Thinkstock
Mike’s cousin, Chandra, works as a waitress in a small restaurant in their community. She enjoys her work and is always polite and friendly when taking orders and serving customers.
“I think it’s important to treat everyone who comes to eat at our restaurant with respect!” she tells Mike. “When customers feel welcome, they are more likely to come back or to leave a tip.”
“Do you get to keep the entire tip?” Mike asks.
“Why do you need to know?” Chandra teases.
“Well,” Mike confesses, “it’s for my math project! I’m looking into how various employees in the service industry get paid.”
Lesson Questions
In this lesson you will explore these questions:
What occupations involve tips and commissions?
How do you factor in tips or commissions to calculate gross pay?
What are the advantages and disadvantages of earning all or part of your income through commissions or tips?
Assessment
You will complete the Lesson 5 Assignment Booklet for assessment. Download the Lesson 5 Assignment Booklet and save it in your course folder now. You will receive instructions on how to complete the Assignment Booklet later in the lesson. You will also be prompted to continue working on the Unit 4 Project.
Remember to save all activities, including those that are not part of the Assignment Booklet, in your course folder.
Required Materials and Equipment
You will need your calculator, access to the Internet, and your inquiry skills.
1.25. Page 2
Module 8: Daily Living
Get Started
tip (gratuity): payment for services rendered above and beyond one’s wages
Tips are commonly freely given by the customer. Tips vary in size or percentage. Servers in restaurants are often rewarded for exemplary service through tips.
commission: part of income, usually quoted as a percent of a sale or business transaction
Salespeople often receive part or all of their earnings through commissions.
Have you considered an occupation that involves earning income through tips and commissions? Do you work in a restaurant or clothing store? If yes, then you might already have a job that involves one of these methods of earning income.
It is time to investigate jobs and occupations involving tips or commissions.
Start your exploration by listening to “Salespeople and Minimum Wage.”
In Lesson 4 you examined the minimum wages employees are guaranteed by law. What about people who earn tips?
Example 1
Jolene works as a salesperson at a bicycle shop in Cold Lake, Alberta. Normally she makes a good living being paid only by a commission on her sales. However, last January, sales were slow. Here are her commissions on sales for the four-week period. The same data is displayed in a table and in a graph.
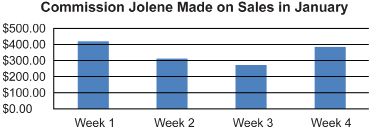
|
Jolene Dumas |
Commissions on Sales |
|
Week 1 |
$415.00 |
|
Week 2 |
$310.20 |
|
Week 3 |
$274.80 |
|
Week 4 |
$385.50 |
What will Jolene’s gross pay be for the month of January? Jolene does not record her hours.
Solution
In week 2 and week 3, Jolene made less than the minimum $352.00/wk to which she is entitled according to the minimum wage in effect in 2010. So, her employer will pay her $352.00 for each of those weeks.
![]()
Jolene’s gross pay for January is $1504.50.
 Self-Check
Self-Check
These questions refer to Example 1.
SC 1. What is the purpose of the law that guarantees Jolene at least $352.00/wk?
SC 2. Suppose Jolene were required by her boss to record her hours. Suppose she worked 40 h each week. What is the minimum her weekly earnings would be?
SC 3. How did the province come up with $352.00/wk as a minimum wage for salespeople who do not record their hours?
1.26. Page 3
Module 8: Daily Living
Explore
 Try This
Try This
For this activity you will need access to the Internet. You will be exploring occupations that pay commissions or involve tips. Work with a partner, if possible.
Prepare lists of occupations involving commissions or tips. You may wish to refer to the list of website addresses you saved in your course folder in Lesson 4. These websites provide information on careers and may give you some ideas.
Remember to add any new website addresses you find to your course folder.
TT 1. List as many occupations as you can in each column. Add to these lists when you share your results with your fellow students.
Occupations That Earn Commissions |
Occupations That Earn Tips |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
TT 2. Why do you think employers reward their salespeople with commissions?
TT 3. What are some advantages to being paid a commission? What are some disadvantages?
TT 4. What do you think is a fair tip to give your server in a restaurant? Why?
 Share
Share
Share and discuss your answers to the Try This questions TT1–4. Summarize your discussion by answering the following question “Commission or no commission—how would you rather be paid?” in a short paragraph.
Save a copy of this paragraph in your course folder.
1.27. Page 4
Module 8: Daily Living
Bringing Ideas Together
In Get Started and Explore you examined occupations involving commissions and tips. Commissions and tips generally involve percents. Many salespeople receive a monthly salary and a percent commission on gross sales.
Work through the following examples.
Example 2

© Tan Kian Khoon/144976/Fotolia
Jaime is a salesperson at Boats and Motors. She receives a base salary of $1500.00/mo and a 2% commission on gross sales. Last month, her gross sales were $205 000.00. What was Jaime’s gross pay?
Solution

base monthly salary = $1500.00
gross sales = $205 000.00
commission rate = 2%
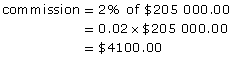
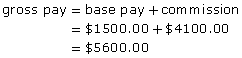
Jaime’s gross pay was $5600.00.
Example 3
Arnold Bossio is starting up a sports shop in northwestern Saskatchewan. He will soon be advertising for salespeople. Arnold has researched the market in his area and forecasts that each of his salespersons will have annual sales of $750 000.00. Arnold believes the annual gross pay of a salesperson should be $60 000.00. He intends to pay each salesperson a base salary of $2000.00/mo. At what rate should Arnold set commissions for the salespersons he hires? Round to one decimal place.
View the animated “Example 3 Solution: Setting a Commission Rate.”
Why Have Commissions?
Commissions serve as a motivator. Management generally believes that paying sales staff a commission on sales will encourage employees to work hard to achieve sales targets. However, commissions can also have a negative effect on staff and customer relations. Competition among staff for customers must be managed carefully to prevent hard feelings.
 Self-Check
Self-Check
These questions may or may not involve a base salary. However, there is a single commission rate in each case.
© iofoto/5266170/Fotolia
SC 4. Jenn is on the sales staff at a bridal shop. She receives a base wage of $8.80/h and 6% commission on all sales. Yesterday she worked 7.75 h and her sales were $2750.00. What was Jenn’s gross pay for yesterday?
SC 5. Paula is a real-estate broker. She has just sold a $150 000.00 condominium to a young couple. The commission was 7%.
-
What was the total commission, in dollars, on the sale?
-
The commission is divided between the listing agent (the broker who put the condo up for sale) and the agent who sells the property. The agent who sells the property receives 60% of the commission. What is Paula’s share of the commission?
-
If 25% of what Paula receives goes to office expenses, how much will Paula have left?
SC 6. Gregory is a hairstylist. He is paid a wage of $12.00/h and receives a 20% commission on hair supplies. On Saturday, Gregory worked 7.50 h and sold $270.00 of hair supplies. Before tips, what were Gregory’s earnings?
Tips
To this point in this lesson, you have explored commissions. Employees in the service industry, such as servers, bellhops, housekeepers, taxi drivers, hairstylists, and barbers, often receive tips in the course of performing their duties.
In restaurants, servers are often rewarded for good service. Customers often determine tips as an approximate percent of their bill. Standard tips for good service are often in the 12%-to-15% range.
Tips seem like a good thing, but some employers factor in tips when they set a worker’s wage. So, often servers are paid little more than minimum wage on the assumption that customers’ tips will make up the difference.
Example 4
Debby is a waitress in a local restaurant. She has just served a family of four. The bill, before taxes, comes to $125.40. Her tip was approximately 12% of the total. Calculate her tip to the nearest dollar.
Solution
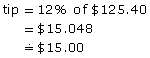
 Self-Check
Self-Check
In the next set of questions you will problem solve based on your knowledge of tips.
SC 7. Lunay is a server at a family restaurant. She is paid the minimum wage of $8.80/h for a regular 8-h shift. On an average shift she serves customers whose bills total $900.00. She regularly receives 15% in tips.
- What would Lunay’s gross earnings be for one day?
- With tips, what does Lunay earn per hour?
SC 8. A party of three is at a restaurant, and their bill totals $87.00 before taxes. The GST (5%) is $4.35. How could you use the GST to calculate a tip of 15%?
 Mastering Concepts
Mastering Concepts
Nadia is a sales representative. Her monthly salary is $3000.00, and she receives a 4% commission on her gross sales. She would like to earn $70 000.00 this year. What would Nadia’s annual gross sales have to be?
1.28. Page 5
Module 8: Daily Living
Lesson Summary

© Konstantin Sutyagin/6605730/Fotolia
Vijay is a salesperson at a men’s clothing store. Each year he looks forward to the Christmas season. From mid-November on, sales pick up and business is good. Vijay does not own the business; instead, he is an employee. He earns a base salary and receives commissions on his sales. The percentage he receives as commission increases with increased sales. Do you know the standard commissions salespeople receive?
In this lesson you answered these questions:
- What occupations involve tips and commissions?
- How do you factor in tips or commissions to calculate gross pay?
- What are the advantages and disadvantages of earning all or part of your income through commissions or tips?
Check your level of understanding of the materials covered in this lesson by completing “Lesson 5 Traffic Lights.” If you select an amber or red traffic light in the multimedia piece, you will receive information about additional work you can complete to improve your understanding of the topics. Complete the suggested work before you proceed to the Lesson 5 Assignment. If you experience difficulty, contact your teacher before starting the Lesson 5 Assignment.
In Lesson 5 you examined commissions and tips. Both are applications of percents. Commissions are a percent of gross sales, and tips are often calculated as a percent of the bill. Both commissions and tips are used to supplement income. Do you remember the advantages and disadvantages of each?
 Assignment
Assignment
Retrieve the Lesson 5 Assignment Booklet you saved in your course folder at the start of this lesson. Complete the Assignment Booklet.
Resave your Assignment Booklet in your course folder and submit a copy to your teacher for assessment.
Unit 4 Project
Before you move on to the next lesson, you should continue your research for your Unit 4 Project. Have you contacted an employee you can interview who works in the job or career you are going to explore? Has this lesson helped you come up with questions you can ask about this person’s job and how she or he earns income? For more information about this step and later steps of the task, review the Unit 4 Project.
1.29. Lesson 6
Module 8: Daily Living
Lesson 6: Being Paid on the Job: Piecework and Contracts
Focus

University of Saskatchewan Archives, Institute for Northern Studies (INS) fonds – F2100. Slide 3129
Do you have an Inuit soapstone carving or a First Nations artist’s print in your home? Through their work, First Nations and Inuit artists depict their natural and spiritual worlds.
Their art has become highly respected and sought after by collectors around the world. To protect the interests of the artists, co-operatives have been formed in their communities.
In the photograph, Northern artists are working in a pottery co-operative. These co-operatives provide a workspace and an outlet through which the artists’ work can be sold. The income these artists earn helps support the artists’ families and communities. Cape Dorset, Nunavut, for example, takes such pride in its artists that it refers to the community as the “Capital of Inuit Art.”
Did You Know?
Most Inuit carvings are not made from soapstone, which is very soft and scratches easily. Rather, most carvings are from serpentinite, which comes in various colours and can take a high polish.
In this lesson you will explore alternative ways of earning income. The income earned by artists is just one example.
Lesson Questions
In this lesson you will explore these questions:
- How do some people earn income through piecework, custom work, contracts, or self-employment?
- What are the advantages and disadvantages of earning all or part of your income through these alternative methods?
Assessment
You will complete the Lesson 6 Assignment Booklet for assessment. Download the Lesson 6 Assignment Booklet and save it in your course folder now. You will receive instructions on how to complete the Assignment Booklet later in the lesson. You will also be prompted to start working on the Unit 4 Project.
Remember to save all activities, including those that are not part of the Assignment Booklet, in your course folder.
Required Materials and Equipment
You will need your calculator, access to the Internet, and your inquiry skills.
1.30. Page 2
Module 8: Daily Living
Get Started
Have you considered an occupation that involves earning income through art? Because of their love of art and their desire to share their talents with others, artists seldom pursue their artistic careers based only on how much money they will earn. Nevertheless, earning an income is an important consideration.
In Example 1 you will consider how the length of time to create a work of art translates into hourly income. The scenario involves custom work.
Example 1
An art collector has approached an Inuit carver with a request for a stone carving similar to one the collector has seen in a photograph. The carver estimates it will take him 20 h to complete the carving. If the artist wishes to earn $25.00/h for his work, what is the minimum the artist should charge the collector? Use a table like the one shown here to organize your data.

Hemera Technologies/PhotoObjects.net/Thinkstock
|
Completion Time |
|
|
Desired Hourly Wage |
|
|
Carving Selling Price |
|
Solution
|
Completion Time |
20 |
|
Desired Hourly Wage |
$25.00 |
|
Carving Selling Price |
$500.00 |
*Artists will factor in material and tool costs as well.
20 h × $25.00/h = $500.00
 Self-Check
Self-Check
Work with a partner, if possible. The question refers to Example 1.
SC 1. If you are interested in art as a career, what questions might you ask an artist about how she sets a price for her work?
1.31. Page 3
Module 8: Daily Living
Explore
For this activity you will need access to the Internet. You will work through Example 2, and then you will explore occupations paid through piecework.
If you sew or tailor clothes, you might be paid by a clothing manufacturer for each article of clothing you sew.

© poco_bw/7692654/Fotolia

Courtesy of www.Replant.ca. Reproduced with permission.
Some occupations that involve piecework include newspaper carriers, flyer-delivery workers, some telemarketers, and tree planters in Canada’s forests.
Example 2
In the forests of Western Canada, forestry firms and governments replant areas that have been clear-cut or burned over. Tree planters are paid per seedling they plant, and their earnings can vary between $0.08 and $0.25 per tree.
Planting is extremely hard work, and every day worked can be compared to running a marathon. Other hazards include insects, bad weather, and the occasional bear. Tree planters can plant an average of 1500 trees per day.
- If Ethyl plants 1500 trees each day, what would she earn at $0.08/seedling? And at $0.25/seedling?
- Jasper works for a forestry company and is paid $0.15/seedling. To earn at least $250.00/d, how many seedlings would he have to plant?
Solution
- Ethyl plants 1500 seedlings/d.
At $0.08/seedling, Ethyl would earn 1500 × $0.08 = $120.00/d.
At $0.25/seedling, Ethyl would earn 1500 × $0.25 = $375.00/d.
- Jasper is paid $0.15 per seedling.
To earn at least $250.00, Jasper must plant $250.00 ÷ $0.25 = 1666.6666 . . . , or 1667 trees.
 Try This
Try This
It is time for you to do some research on the Internet or by contacting local businesses or employees! Use your investigative skills to answer these questions. Work with a partner, if possible.
TT 1. Make a list of as many occupations you can think of that are paid by piecework. A few examples have been provided.
| Occupation | Product (Unit) by Which Worker Is Paid |
Rate per Product (Unit) |
| tree planters | seedling planted | $0.08 to $0.25 |
| newspaper carrier | paper delivered | What is the rate in your community? |
TT 2. Choose at least two occupations paid by piecework, other than tree planting. Describe the working conditions and expected monthly earnings for each occupation.
TT 3. What are some advantages of being paid by piecework? What are some disadvantages?
 Share
Share
Share your answers to TT 1 to TT3. Compare your list of occupations with other students, and add to your list if possible. Which of the student responses to TT 2 did you find interesting or unexpected?
TT 4. Summarize your discussion by answering the following question in a short paragraph: Would you want to be paid through piecework? Explain your answer.
Save a copy of your response in your course folder.
1.32. Page 4
Module 8: Daily Living
Bringing Ideas Together

© S.White/4810030/Fotolia
In Get Started and Explore, you examined two alternative ways of earning income—custom work and piecework. In this part of the lesson, you will discuss these options further and explore additional methods of earning income.
Example 2
Leslie is a newspaper carrier for the Daily Holler. The newspaper is printed seven days a week and must be delivered by 7:00 a.m. each morning. Leslie is paid $0.10 per paper delivered each day. In August, Leslie had 225 customers. How much did Leslie earn in August?
Solution
There are 31 days in August. Each day, Leslie delivered 225 papers.
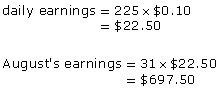

© Stephen Coburn/11256565/Fotolia
 Self-Check
Self-Check
These questions are related to piecework.
SC 2. Use the information from Example 2. What are Leslie’s hourly earnings if it takes 2.5 h/d to deliver the newspapers?
SC 3. Duncan delivers pizza. He is paid $1.50/delivery and keeps all his tips. Last night Duncan made 21 deliveries and received $51.00 in tips. If he worked 5 h, what were his hourly earnings?
Working for Yourself
self-employed: working for yourself instead of for an employer
contract: a legal agreement between a person offering services and a customer
The last category of earners you will explore are the self-employed.
Many workers and professionals, such as lawn-care specialists, tree trimmers and arborists, roofers, painters, electricians, plumbers, drywallers, tutors, accountants, authors, and consultants, decide to work for themselves rather than having an employer.
The self-employed often enter into contracts with their customers or clients.
A contract will specify the tasks to be completed and how the contractor will be paid. The contractor could be paid by the hour or by the job.

© Natali_ua/14333899/Fotolia
Example 3
Bruno is a self-employed painter. He is bidding on a contract to paint the home of a long-term customer. Bruno estimates the job will take 8 d. He has a helper whom he will pay an hourly wage of $10.00/h. If both Bruno and his helper work 8 h each day, and the cost of paint and supplies will be $560.00, what should Bruno charge the customer to end up with $25.00/h for himself?
Solution
The job will take 8 d at 8 h per day, or 64 h.
![]()
cost of paint and supplies = $560.00
![]()
Bruno’s hourly wage = $25.00/h
For 64 hours,
![]()
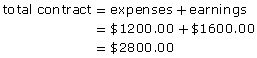
Bruno will say the job will cost the customer $2800.00.
 Self-Check
Self-Check

Hemera/Thinkstock
These questions involve self-employed earnings.
SC 4. Evan is a self-employed plumber. To install a toilet for a customer who wants a particular model, he will charge $90.00. If he supplies the toilet, he will charge $472.00 (before taxes) for the toilet and installation. If Evan can purchase the model of toilet wholesale for $255.00, how much more will he make if he sells the customer the toilet?
SC 5. What are the advantages of self-employment? What are the disadvantages?
 Mastering Concepts
Mastering Concepts
Holly Fine-Day is in the final stages of opening a pizza parlour in a small city in Saskatchewan. She intends to hire a delivery person for the hours between 5:00 p.m. and 11:00 p.m.
She is trying to decide whether to pay minimum wage ($9.25/h in Saskatchewan as of February 2010) or to contract out the delivery to a self-employed driver for $2.50/delivery. She wants to attract a responsible person who will work for her for a long time. If Holly asked you for advice, what would you recommend?
1.33. Page 5
Module 8: Daily Living
Lesson Summary

© Ken Hurst/746114/Fotolia
Last summer, Mike worked for a landscaping firm. He cut lawns when the weather permitted, and he was paid minimum wage. This summer, Mike is considering working on his own. He plans to place flyers advertising his lawn-care services in mailboxes in his community. What factors should Mike take into account to make the right decision to maximize his income?
Self-employment was just one of the alternate ways of earning income that you explored in this lesson. You explored the following questions:
- How do some people earn income through piecework, custom work, contracts, or self-employment?
- What are the advantages and disadvantages of earning all or part of your income through these alternative methods?
Check your level of understanding of the materials covered in this lesson by completing “Lesson 6 Traffic Lights” If you select an amber or red traffic light in the multimedia piece, you will receive information about additional work you can complete to improve your understanding of the topics. Complete the suggested work before you proceed to the Lesson 6 Assignment. If you experience difficulty, contact your teacher before starting the Lesson 6 Assignment.
You examined self-employment as an alternative to working for an employer. You also explored piecework and custom work. Do you remember the advantages and disadvantages of each of these alternative methods of earning income?
 Assignment
Assignment
Retrieve the Lesson 6 Assignment Booklet you saved in your course folder at the start of this lesson. Complete the Assignment Booklet.
Resave your Assignment Booklet in your course folder and submit a copy to your teacher for assessment.
Unit 4 Project
Before you move on to the next lesson, you should continue your research for your Unit 4 Project. Have you contacted an employee you can interview who works in the job or career you are going to explore? Has this lesson helped you come up with questions you can ask about how this person earns income? For more information about this step and later steps of the task, review the Unit 4 Project.
1.34. Lesson 7
Module 8: Daily Living
Lesson 7: Deductions and Net Pay

© John Tomasell/2939858/Fotolia
Focus
Mike is interviewing a young mechanical engineer as part of his Unit 4 Project. Listen to their conversation in “Mike and Amina.”
In this lesson you will explore deductions and take-home pay.
Lesson Questions
You will explore these questions:
What is net pay, and how is net pay calculated?
How are Canada Pension Plan, Employment Insurance, and income tax deductions calculated?
Assessment
You will complete the Lesson 7 Assignment Booklet for assessment. Download the Lesson 7 Assignment Booklet and save it in your course folder now. You will receive instructions on how to complete the Assignment Booklet later in the lesson. You will also be prompted to continue working on the Unit 4 Project.
Remember to save all activities, including those that are not part of the Assignment Booklet, in your course folder.
Required Materials and Equipment
You will need your calculator, access to the Internet, and your inquiry skills.
Get Started
In the last few lessons in this module you explored various methods of earning income. You learned how to calculate gross income in each case. However, when you receive your first paycheque from your job, you will notice that you do not receive all your gross pay.
Various amounts, such as union dues, taxes, and pension-plan contributions, are subtracted. These amounts are detailed on your paycheque under the category of deductions.
Explore these deductions in “Paystub Explained.”
1.35. Page 2
Module 8: Daily Living
Explore
Calculating Canada Pension Plan (CPP) Contributions
First you will investigate how Canada Pension Plan (CPP) contributions are calculated.
If you are between 18 and 70, work in a pensionable occupation, and do not yet receive a CPP or Québec pension, you must contribute to the Canada Pension Plan. The Canada Revenue Agency provides a table of contribution rates, maximums, and exemptions. The Canada Revenue Agency is the tax-collection arm of the Canadian government.
Go to the Canada Revenue Agency’s website now, and look at this table. To find the website, you will need to do an Internet search using the following terms: “CRA-ARC CPP Table of Contribution Rates,” and you may need to search the CRA website for the actual table. Remember that you can ask your teacher for help finding the table.
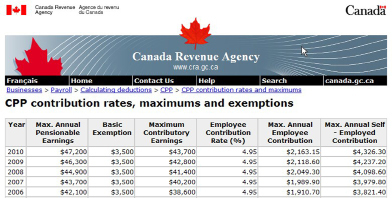
Source: Canada Revenue Agency. Reproduced with permission of the Minister of Public Works and Government Services Canada, 2010.
The following rules were applied in 2010 to determine how much CPP contributions a person must make:
-
You don’t have to pay any CPP contributions on the first $3500.00 you make (subtract $3500.00 from your gross annual income).
-
You pay 4.95% in CPP contributions on the leftover income, and your employer pays 4.95%. If you are
self-employed you pay 9.90%.
-
Once you have made $47 200.00, you have hit the maximum—no more CPP contributions will be deducted from the rest of your earnings in that year.
A table like this can be used to work through these calculations.
|
A |
gross annual income ($47 200 if income is over $47 200) |
$36 000.00 |
|
B |
exempt earnings |
–$3500.00 |
|
C |
contributory earnings (amount A – amount B) |
$32 500.00 |
|
D |
contribution rate (%) |
4.95% (9.90% if self-employed) |
|
E |
contribution rate (decimal) |
0.0495 (0.099 if self-employed) |
|
F |
annual CPP contributions (amount C × amount E) |
$1608.75 |
|
G |
monthly CPP contributions (amount F ÷ 12) |
$134.06 |
Work through the following example to see how each step in the CPP calculation is completed.
Example 1
Benny is a city employee. Benny’s gross annual income in 2010 was $36 000.00. What were Benny’s annual CPP contributions? What were Benny’s monthly contributions?
|
A |
gross annual income ($47 200 if income is over $47 200) |
$ |
|
B |
exempt earnings |
–$3500.00 |
|
C |
contributory earnings (amount A – amount B) |
$ |
|
D |
contribution rate (%) |
4.95% (9.90% if self-employed) |
|
E |
contribution rate (decimal) |
0.0495 |
|
F |
annual CPP contributions (amount C × amount E) |
$ |
|
G |
monthly CPP contributions (amount F ÷ 12) |
$ |
View the animated “Example 1 Solution: CPP Calculations.”
Example 2
If Benny were self-employed and earned $36 000.00, what would his contributions have been?
Solution
If Benny were self-employed, his annual contribution rate would be 9.90%, which is double an employee’s rate.
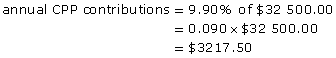
Note: $3217.50 = 2 × $1608.75
Example 3
June is an employee. In 2010, she earned $62 125.00. What were June’s annual CPP contributions? What were June’s monthly contributions?
Solution
|
A |
gross annual income ($47 200 if income is over $47 200) |
$47 200.00 |
|
B |
exempt earnings |
–$3500.00 |
|
C |
contributory earnings (amount A – amount B) |
$43 700.00 |
|
D |
contribution rate (%) |
4.95% (9.90% if self-employed) |
|
E |
contribution rate (decimal) |
0.0495 (0.099 if self-employed) |
|
F |
annual CPP contributions (amount C × amount E) |
$2163.15 |
|
G |
monthly CPP contributions (amount F ÷ 12) |
$180.26 |
Row A: $62 125.00 is greater than the maximum of $47 200.00. Use $47 200.00.
Row B: The first $3500.00 of earnings are exempt.
Row C: ![]()
Row D: As an employee, her contribution rate was 4.95%.
Row F: 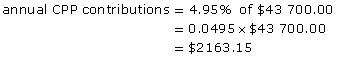
June’s employer would contribute another $2163.15 on June’s behalf.
Row G: 
 Self-Check
Self-Check
The following questions use CPP rates from 2010.
SC 1. Jerome was an employee in 2010. In 2010, he earned $27 140.00. What were his annual CPP contributions? What were his monthly contributions?
SC 2. If Jerome were self-employed, what would his annual contributions be?
SC 3. Christian is paid biweekly by her employer. Her biweekly gross pay is $1230.75. What are her biweekly CPP contributions?
1.36. Page 3
Module 8: Daily Living
Calculating Employment Insurance Premiums
Next you will investigate how Employment Insurance (EI) premiums are calculated.
Like CCP contributions, there are maximum annual earnings on which premiums are calculated. The Canada Revenue Agency provides tables to show how premiums are calculated. These tables can be found on the CRA website. Find the tables now by searching the Internet using the following terms: “CRA-ARC EI Premium Rates and Maximums.” Again, you may have to search the CRA website to locate the actual tables.
If you look at the Canada Revenue Agency’s tables for 2010, the maximum insurable earnings were $43 200.00. But, unlike CPP contributions, there is no minimum. The contribution rate is 1.73% for employees (1.36% in Québec). Employers pay 1.4 times the employee’s contribution.
The self-employed may choose to contribute. Their contribution rate is the same as the rate for employees. However, self-employed people cannot receive unemployment benefits; they may receive maternity benefits. Unemployment benefits are voluntary for the self-employed but mandatory for employees.
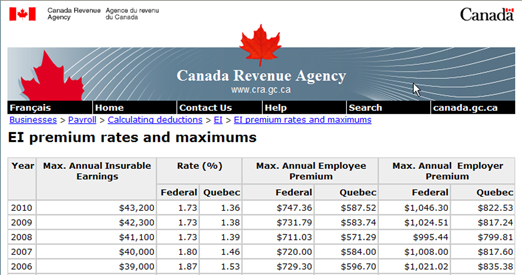
Source: Canada Revenue Agency. Reproduced with permission of the Minister of Public Works and
Government Services Canada, 2010.
Example 4
Kwok and Félix both work for the same employer in British Columbia. Kwok’s annual salary in 2010 was $37 000.00, and Félix’s salary was $45 000.00. What were their EI premiums in 2010?
Solution
Kwok’s annual salary of $37 000.00 was less than the maximum insurable earnings ($43 200.00).
So,
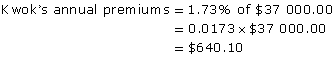
Félix’s annual salary of $45 000.00 was more than the maximum insurable earnings of $43 200.00. In this case, use the maximum of $43 200.00 in place of Félix’s annual salary. So,
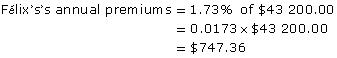
 Self-Check
Self-Check
The following questions use EI rates from 2010.
SC 4. Eduarta works in Montréal. In 2010, her annual salary was $29 250.00. What were her monthly EI premiums?
SC 5. If Eduarta had worked in Saskatoon for the same salary, what would her monthly premiums have been?
SC 6. Marvin lives in the Yukon. He is paid semimonthly by his employer. His semimonthly gross pay is $1330.00. What are his semimonthly EI premiums?
Calculating Income Tax Deductions
Income tax deductions from your gross earnings are not as simple to calculate as CPP contributions or EI premiums. There is not a single rate for all earners. Tax rates increase as your income increases. Your tax also varies depending on your personal circumstance—whether you are married or single, have children or not, and so on!
When you are first hired, your employer will ask you to fill out a form. The form will help the employer decide what category you fall into. This lets your employer know how much income tax to deduct from your pay on behalf of the Canada Revenue Agency.
This form is called the TD11. TD stands for Tax Deduction. Take a brief look at a TD1 to see how the form is set up.
1 Source: Canada Revenue Agency. Reproduced with permission of the Minister of Public Works and Government Services Canada, 2010.
The TD1 form is not the only form you will complete as a new employee. You will also complete a form for the province or territory in which you are working. Once you have completed these forms, you will be assigned a claim code from 0 to 10 for federal tax as well as a claim code for provincial tax.
The claim code for a single person with no other deductions is usually Claim Code 1. A married person who supports people in addition to oneself will have a higher claim code and will not have as much deducted in tax.
Your employer has several methods to determine the tax withheld. These methods include tax tables, computerized calculations, and online tax calculators.
The following is a portion of the 2010 federal tax table for employees paid monthly.
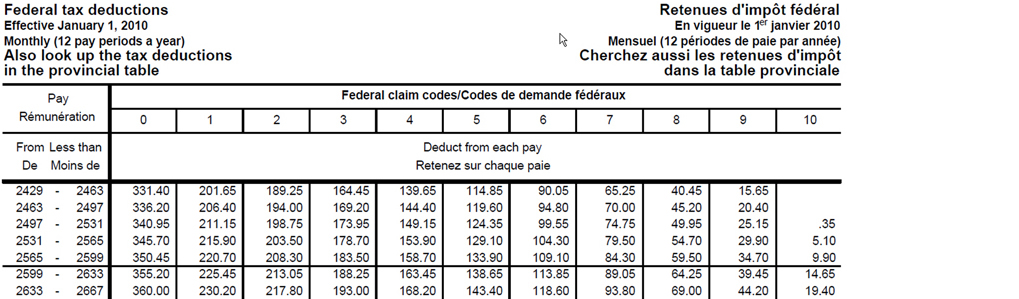
Source: Canada Revenue Agency. Reproduced with permission of the Minister of
Public Works and Government Services Canada, 2010.
Look at the first row in this portion of the table. For employees with Claim Code 1 who make between $2429.00 and $2463.00 monthly, $201.65 is deducted in federal tax. Move across the applicable row in the table, and you will see that the higher the claim code, the lower the tax. This is also true for provincial taxes.
The portion of the Alberta tables shown applies to employees paid semimonthly. Again, if you go across any of the rows, you will see that the higher the claim code, the less tax that is deducted.
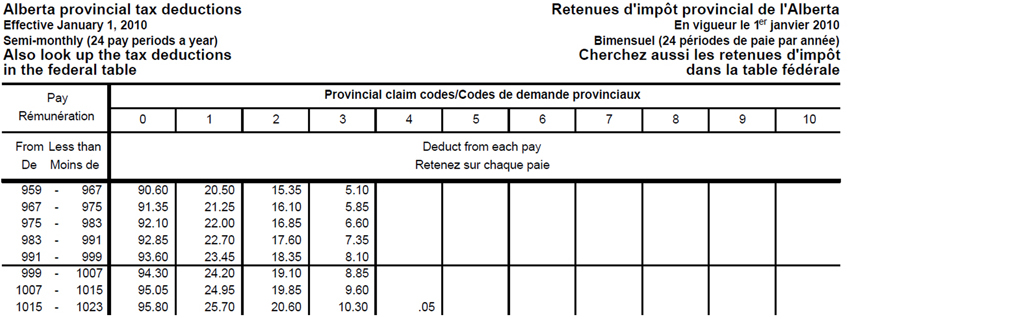
Source: Canada Revenue Agency. Reproduced with permission of the Minister of
Public Works and Government Services Canada, 2010.
Study this example.
Example 5
Amina works in British Columbia. Her employer has determined that her category for both federal and provincial taxes is Claim Code 1. She is paid $574.27 weekly. The 2010 tax tables shown in the solution will be used to answer the following questions. What is the federal tax deducted? What is the provincial tax deducted? What is the total tax deducted?
Solution
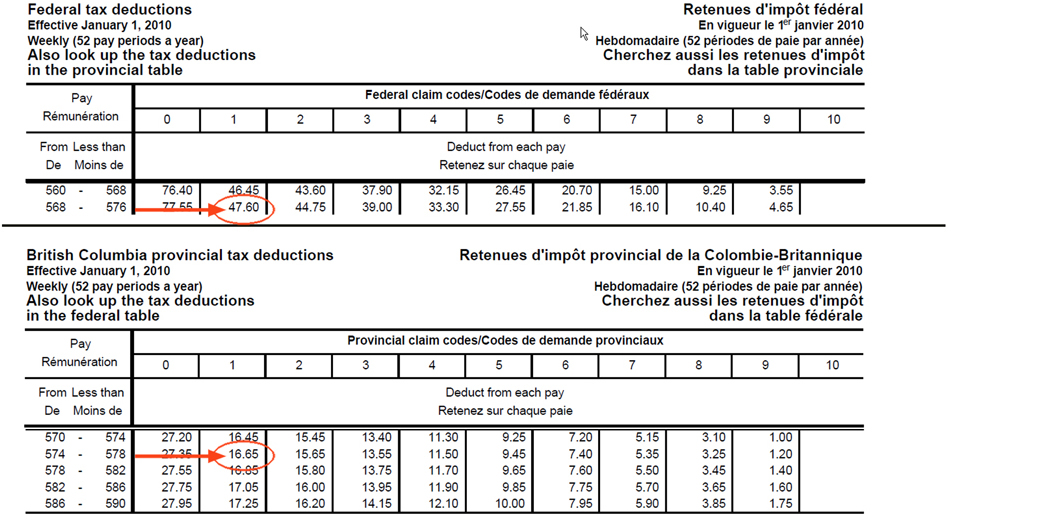
Source: Canada Revenue Agency. Reproduced with permission of the Minister of
Public Works and Government Services Canada, 2010.
From the tax tables, for the year 2010, the following rates apply: federal tax = $47.60 and provincial tax = $16.65. The total income tax is $64.25.
In this lesson you’ve seen CPP contributions, EI premiums, and income tax deductions calculated using tables. However, most calculations are performed by computer software, such as the Payroll Deductions Online Calculator from the Canada Revenue Agency.
For the next activity, you will need access to the Internet. You will explore net income using the Payroll Deductions Online Calculator. This calculator determines the amount of CPP contributions, EI premiums, and federal and provincial/territorial income taxes to be deducted from gross income.
1.37. Page 4
Module 8: Daily Living
 Try This
Try This
Work with a partner, if possible.
The Online Payroll Deductions Calculator may be found by entering the following terms into an Internet search engine: CRA Payroll Deductions Online Calculator. If you need help locating the calculator, ask your teacher.
Once you find the calculator, bookmark the web page for easy access. This calculator will help you determine CPP, EI, and income tax deductions from gross salary.
Study these examples to see how to use the Online Payroll Deductions Calculator.
Example 6
In 2010, Evangeline worked in Yorkton, Saskatchewan. She received a gross salary from her employer of $4520.00/mo. She fell under Claim Code 1. Use the online calculator to determine her monthly CPP contributions, EI premiums, and federal and provincial taxes. Determine her net monthly income.
View and carefully follow the steps in “Example 6 Solution.”
So, Evangeline’s net monthly pay was $3285.08. Evangeline’s deductions are as follows:
|
CPP Contribution |
$209.30/mo |
|
EI Premium |
$78.20/mo |
|
Federal Tax |
$576.11/mo |
|
Provincial Tax |
$371.31/mo |
|
Total Deductions |
$1234.92/mo |
Did you know there are circumstances that can reduce the income taxes owed? In Example 7 you will meet Perry. Perry earned income in the Northwest Territories. He made the same salary as Evangeline. However, because he works in the North, Perry’s taxable income is reduced.
Example 7
In 2010, Perry worked in Yellowknife, NWT. He received a gross salary from his employer of $4520.00/mo. He was listed under Claim Code 1. He lived in an apartment with two friends and shared expenses. Use the online calculator to determine Perry’s monthly CPP contributions, EI premiums, and federal and provincial taxes. Determine Perry’s net monthly income.
View and carefully follow the steps in “Example 7 Solution.”
So, Perry’s monthly net pay was $3504.91. His deductions were as follows:
|
CPP Contribution |
$209.30/mo |
|
EI Premium |
$78.20/mo |
|
Federal Tax |
$520.90/mo |
|
Provincial Tax |
$206.69/mo |
|
Total Deductions |
$1015.09/mo |
Notice the CPP and EI deductions are the same as they were for Evangeline in Saskatchewan, but the federal tax is less. This is because of Perry’s reduced taxable income for northern residency. Also, the territorial tax was less for two reasons: the taxable income was less, and the Northwest Territories’ tax rates are different from Saskatchewan’s.
Now it is your turn to explore the CRA Payroll Deductions Online Calculator.
TT 1. Complete the following table using the CRA Payroll Deductions Online Calculator. Set the date on the calculator for the current year!
|
Name |
Gross Income |
Province |
Claim Code |
Taxable Income |
CPP Contribution |
EI Premium |
Federal Tax |
Provincial/ Territorial Tax |
Net Pay |
|
Clive |
$3200.00/mo |
AB |
1 |
$3200.00/mo |
|||||
|
Lil |
$925.00/wk |
MB |
1 |
$925.00/wk |
|||||
|
Tom |
$2700.00 biweekly |
BC |
2 |
$2700.00 biweekly |
|||||
|
Wing |
$2100.00 semimonthly |
YT |
1 |
||||||
|
John |
$5200.00/mo |
NU |
3 |
TT 2. Tina lives in Alberta and is paid a monthly salary by her employer of $2400.00. Her claim code is 1.
- What is Tina’s net pay per month?
- Tina had been hoping to receive a raise of $100.00/mo. If her salary had been $2500.00, what would Tina’s take-home pay have been? Would it have been $100.00 more? How can you explain this result?
 Share
Share
Once you have completed TT 1 and TT 2, discuss the following questions with a partner or group:
Why is it important to ensure the appropriate period of required salary or commission is selected when using the CRA Payroll Deductions Online Calculator?
-
Why do you think the CRA developed, at their own expense, the Payroll Deductions Online Calculator for employers and other taxpayers?
After your discussion, place your answers to TT 1 and TT 2 in your course folder along with the summary of your discussion.
1.38. Page 5
Module 8: Daily Living
Bringing Ideas Together
In Get Started and Explore you examined how Canada Pension Plan, Employment Insurance, and federal and provincial/territorial income tax deductions are determined. You saw that these deductions are subtracted from your gross pay. There are additional deductions that reduce your take-home pay. These could include the following:
union dues
-
company pension plans
-
medical-plan premiums
-
voluntary charitable donations
taxable income: income on which income taxes are calculated
taxable income = gross income – (deductions like union dues + company retirement-plan contributions + Northern residence sums as determined from the TD1 form)
Two of these deductions, union fees and company pension-plan contributions, will reduce your taxable income. In other words, the federal and provincial/territorial taxes are based on your income after these deductions are subtracted from your gross pay. You will remember that Northern residents also qualify for additional deductions from gross income.
Example 8
Georgina works in Hinton, Alberta. Her gross salary in 2010 is $3752.00/mo. She is a union member, so she has $75.00 in union dues deducted from her paycheque each month. She also has $250.00/mo deducted as her contribution towards a company pension. Her employer has determined her claim code to be 1.
- What is Georgina’s monthly taxable income?
- What is Georgina’s net income?
Solution
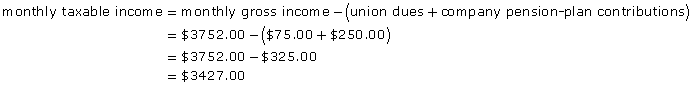
-
View and carefully follow the steps in “Example 8.b. Solution.” The solution is based on the CRA Payroll Deductions Online Calculator with January 1, 2010 set for the period.
 Self-Check
Self-Check
In these questions you will determine problem situations involving net income using the CRA Payroll Deductions Online Calculator.
The solutions provided to you for comparison are based on the CRA Payroll Deductions Online Calculator set for the period January 1, 2010. To allow a direct comparison to the suggested answers, you should set the calculator to the same period.
SC 7. Use the information from Example 7.
What is Georgina’s take-home pay as a percentage of her gross pay? What percent were deductions? Round to the nearest tenth of a percent.
SC 8. Mercy works for a forestry company in British Columbia. Her biweekly salary is $2815.00. Her biweekly contributions to her company’s pension plan are $225.00. Her union dues are $57.00. She also contributes $100.00 to a Registered Retirement Savings Plan (RRSP) through payroll deductions. Finally, she contributes $45.00 in medical-plan premiums.
Mercy’s claim code is 2. What is Mercy’s biweekly take-home pay?
Hint: RRSP contributions reduce her taxable income, but medical-plan premiums do not.
SC 9. Using the results of SC 8, calculate what percent the income tax (federal and provincial combined) is of Mercy’s
- gross earnings
- taxable earnings
Round your answers to the nearest tenth of a percent.
SC 10. Matty works for a firm in Regina, Saskatchewan. In January 2010, Matty received $5400.00 in salary. In February, Matty received a 10% increase in pay. Will Matty’s take-home pay increase by 10%? Why or why not?
Use the CRA Payroll Deductions Online Calculator to help you answer this question. Assume that EI, CPP, and income taxes are Matty’s only deductions. Matty is taxed under Claim Code 1.
 Mastering Concepts
Mastering Concepts
In this lesson you discovered that the income on which you pay income tax is reduced by your company pension-plan contributions and Registered Retirement Savings Plan contributions. Why do think those who make these contributions pay less in income tax than those who do not make these contributions?
1.39. Page 6
Module 8: Daily Living
Lesson Summary

© JOSEPH SL TAN MATT/11282381/Fotolia
Net income, or take-home pay, is what is left of your gross earnings after deductions. Three of these deductions are Canada Pension Plan contributions, Employment Insurance premiums, and income taxes. These are collected by the Canada Revenue Agency and are based on percentages of your earnings.
Other deductions depend on your employment situation. These deductions may include union dues, and company pension contributions. Some deductions are voluntary, such as RRSP contributions and charitable donations.
In this lesson you explored the following questions:
What is net pay, and how is net pay calculated?
How are Canada Pension Plan, Employment Insurance, and income tax deductions calculated?
Check your level of understanding of the materials covered in this lesson by completing “Lesson 7 Traffic Lights.” If you select an amber or red traffic light in the multimedia piece, you will receive information about additional work you can complete to improve your understanding of the topics. Complete the suggested work before you proceed to the Lesson 7 Assignment. If you experience difficulty, contact your teacher before starting the Lesson 7 Assignment.
You investigated how percentages are used to calculate CPP contributions and EI premiums. You discovered that income taxes can be determined using tables or computer software. One of the tools that enabled you to determine all three of these deductions was the Canada Revenue Agency Payroll Deductions Online Calculator. This CRA tool can be used by the employer to determine an employee’s net income or by the employee to calculate take-home pay!
 Assignment
Assignment
Retrieve the Lesson 7 Assignment Booklet you saved in your course folder at the start of this lesson. Complete the Assignment Booklet.
Resave your Assignment Booklet in your course folder and submit a copy to your teacher for assessment.
Unit 4 Project
This is the final lesson in this module, so you should be close to finishing your Unit 4 Project. Has this lesson helped you come up with questions you can ask about how much your take-home pay might be as a person starting the job or career you’re investigating? For more information about this step and later steps of the task, review the Unit 4 Project.
1.40. Module 8 Summary
Module 8: Daily Living
Module 8 Summary

Photos.com/Thinkstock
The Royal Canadian Mint, with facilities in Winnipeg and the Ottawa region, mints (makes) everyday circulation and collector coins for Canada. The Winnipeg facility, shown here, mints over 1 billion coins a year, not only for Canada but also for countries in Asia, Africa, Europe, and the Caribbean. In 2010, the Royal Canadian Mint was chosen as one of the top 100 employers for maintaining a positive workplace!
The coins in your pocket or purse are a means of exchange—a way to exchange your labour in the workplace for goods and services for daily living.
Throughout Module 8 you examined how the concepts from these lessons applied to an occupation or career you may wish to pursue. Regardless of whether you end up in the job you explored in the Unit 4 Project, the skills you acquired in Module 8 are skills for daily living!
A picture can tell a story. The Module 8 Lessons Summary is a collection of images from each lesson that describes the math you explored. What do you remember about each image? Can you relate each image to something new you learned in this module? Watch “Module 8 Lessons Summary” now.