Lesson 2
| Site: | MoodleHUB.ca 🍁 |
| Course: | Math 30-1 SS |
| Book: | Lesson 2 |
| Printed by: | Guest user |
| Date: | Tuesday, 9 December 2025, 11:13 PM |
Description
Created by IMSreader
1. Lesson 2
Module 1: Function Transformations
Lesson 2: Reflections
Focus

Comstock/Thinkstock
A portrait is an interesting way to celebrate people in your life. A strong portrait captivates viewers, causing them to wonder about the person depicted, almost like a visual biography. Proportions of a head will vary from person to person and change slightly with age, but there are some basic principles in creating portraits.
Look at the following diagram of half a face. Suppose you wanted to complete this picture. Could you do it? How would you decide where the other eye should go? Where would you start to draw an ear? Would your strategy work for any half picture?

Lesson Outcomes
At the end of this lesson you will be able to
- determine the relationship between the coordinates of a point and the coordinates of that point reflected across the x-axis or y-axis
- sketch the graph of the functions y = f(−x) and y = −f(x) given the graph of y = f(x)
- determine the equation of a function given its graph, which is a reflection of the graph of y = f(x) through the x-axis or the y-axis
Lesson Questions
You will investigate the following questions:
- How is a point related to its reflection?
- How are the graphs of the functions y = f(x), y = f(−x), and y = −f(x) related?
- How can you graph the function y = f(−x) or y = −f(x) given y = f(x)?
Assessment
Your assessment may be based on a combination of the following tasks:
- completion of the Lesson 2 Assignment (Download the Lesson 2 Assignment and save it in your course folder now.)
- course folder submissions from Try This and Share activities
- additions to Glossary Terms and Formula Sheet
Materials and Equipment
- graph paper
1.1. Launch
Module 1: Function Transformations
Launch
Do you have the background knowledge and skills you need to complete this lesson successfully? Launch will help you find out.
Before beginning this lesson you should be able to determine whether or not a relation is a function.
1.2. Are You Ready?
Module 1: Function Transformations
Are You Ready?
Complete the following questions. If you experience difficulty and need help, visit Refresher or contact your teacher.
Determine whether or not the following relations are functions. Explain your reasoning.
- Set A = {(1, 3), (2, 9), (7, 5), (−2, 8), (−1, 4), (2, −1)} Answer
- Set B = {(1, 2), (2, 9), (−3, 4), (3, 4), (0, 5), (4, −7)} Answer
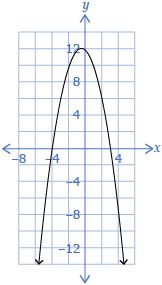
Answer
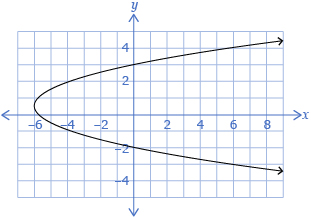
Answer
If you answered the Are You Ready? questions without difficulty, move to Discover.
If you found the Are You Ready? questions difficult, complete Refresher.
1.3. Refresher
Module 1: Function Transformations
Refresher
Review the difference between relations that are functions and relations that are not functions in “Introduction to Functions.”
Go back to the Are You Ready? section and try the questions again. If you are still having difficulty, contact your teacher.
1.4. Discover
Module 1: Function Transformations
Discover
Try This 1
On a piece of graph paper, plot the points (1, 3), (2, 2), (3, 4), and (5, 2) as shown in the diagram.
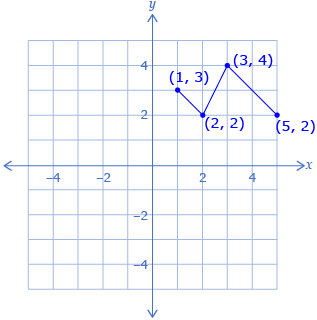
- Imagine using the y-axis as a line of reflection, or a line of symmetry, to reflect the points across the y-axis. Sketch the new image on your graph.
- Reflect your original points across the x-axis and sketch the new image.
- Use the diagrams you created to complete a table like the following.
Coordinates of Original Point
Coordinates After Reflecting Across the y-axis
Coordinates After Reflecting Across the x-axis
(1, 3)
(2, 2)
(3, 4)
(5, 2)
- What relationship do you notice between an original point and that point reflected across the
- y-axis?
- x-axis?
- Was the original figure a function? Are the reflected figures functions?
- Use Reflection Interactive to check your table from question 3.

- The original relation had all points located in the first quadrant. Drag each point of the blue figure so the figure has points in multiple quadrants. Use Reflection Interactive to repeat questions 1 to 5.

![]() Save your responses in your course folder.
Save your responses in your course folder.
Share 1
With a partner or group, discuss the following questions based on the information from Try This 1.
- Did you find the same relationship in question 4?
- Did reflecting a function create a function? Will this always be true? Explain.
- If you reflected a relation that was not a function, would the reflection create a relation that is not a function?
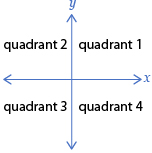
Remember how the quadrants are labelled.
1.5. Explore
Module 1: Function Transformations
Explore
A reflection is a transformation that produces a mirror image of the original figure. The “mirror” line is called the line of reflection. Although any line can be a line of reflection, you will mainly use the x-axis and y-axis in this lesson.
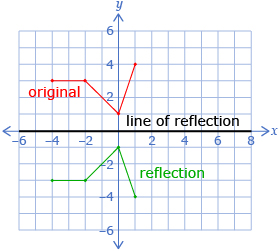
In Try This 1 you may have noticed that reflecting a point across an axis just changed the sign of one of the coordinates. Look ahead to see how this pattern can be formalized.
Try This 2
- Using the information from Try This 1, describe what happens to the coordinates of an individual point as the point is reflected across an axis. Determine a mapping that will represent this.
Line of Reflection
Description
Mapping
y-axis
(x, y) → (__, __)
x-axis
(x, y) → (__, __)
- An invariant point is a point on the graph that remains unchanged after a transformation has been applied to it. What point(s) would you expect to be invariant when reflecting across the
- x-axis?

- y-axis?
- x-axis?
![]() Save your responses in your course folder.
Save your responses in your course folder.
1.6. Explore 2
Module 1: Function Transformations
Mapping a Reflection
The mapping of a reflection across the y-axis can be written (x, y) → (−x, y). Similarly, the mapping for a reflection across the x-axis is (x, y) → (x, −y).
Be careful when interpreting a reflection across the x-axis. This will cause a change to the y-coordinate of the point. Similarly, reflecting across the y-axis causes a change to the x-coordinate.
Self-Check 1
- The point (5, −6) is reflected across the x-axis. What are the coordinates of the image? Answer
- The point (−3, −1) is reflected across the y-axis. What are the coordinates of the image? Answer
To this point, you have focused on reflecting individual points. Next you will look at reflecting functions.
Try This 3
- Using technology, plot the function
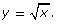

- Using the mapping from Try This 2 as a guide, determine a function that represents
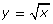 reflected across the
reflected across the
- x-axis
- y-axis

-
In general, what function represents y = f(x) reflected across the
- x-axis?
- y-axis?
![]() Save your responses in your course folder.
Save your responses in your course folder.
Share 2
With a partner or group, compare the equations you determined in Try This 3. What similarities and differences do you see?
1.7. Explore 3
Module 1: Function Transformations
In Try This 3 you may have found that when y = f(x) is reflected across the y-axis, the graph of y = f(−x) is produced. Also, when y = f(x) is reflected across the x-axis, the graph of y = −f(x) is produced.
Read “Example 1” and its solution on pages 18 to 20 of the textbook to view a comparison of the graphs y = f(x), y = −f(x), and y = f(−x).
Self-Check 2
- Complete “Your Turn” from “Example 1” on page 20 of the textbook. Answer
- Complete questions 3, 4, 5.c., 5.d., 7.b., 15.a., 15.b., and C2 on pages 28 to 31 of the textbook. Answer
Add the following terms to your copy of Glossary Terms:
- reflection
- line of reflection
- invariant point
Add the following formulas to your copy of Formula Sheet:
- y = f(−x)
- y = −f(x)
1.8. Connect
Module 1: Function Transformations
Complete the Lesson 2 Assignment that you saved in your course folder at the beginning of this lesson.
![]() Save your responses in your course folder.
Save your responses in your course folder.
Project Connection
There is no Project Connection in this lesson.
Going Beyond
A figure can be reflected across lines that are not the x- or y-axis. Try the following questions.
- What point is produced by reflecting the point (−3, 2) across the line y = 5?
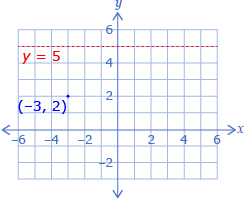
-
- Sketch the function produced when f(x) = x2 is reflected across the line x = 3.
- Write an equation that represents the function drawn in part a.
- What point is produced by reflecting the point (5, 3) across the line y = −2x + 2?

1.9. Lesson 2 Summary
Module 1: Function Transformations
Lesson 2 Summary
A reflection is a transformation that creates a mirror image of the original. A reflection in the x-axis changes all y-coordinates to –y. A reflection in the y-axis changes all x-coordinates to –x. A point that does not change during a transformation is called an invariant.
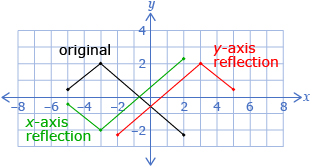
Now is a good time to update your summary table for the reflections you learned in this lesson.
In the next section you will begin to look at stretching a function.