Lesson 4
| Site: | MoodleHUB.ca 🍁 |
| Course: | Math 30-1 SS |
| Book: | Lesson 4 |
| Printed by: | Guest user |
| Date: | Tuesday, 9 December 2025, 11:17 PM |
Description
Created by IMSreader
1. Lesson 4
Module 8: Permutations, Combinations, and the Binomial Theorem
Lesson 4: The Binomial Theorem
Focus
In previous lessons in this module you explored a number of ways in which people are identified. These forms of recognition included phone numbers, passwords, and passports. Remember that personal identification is any data that can be used to identify an individual. A famous mathematician is often identified by the triangle shown.


iStockphoto/Thinkstock
Blaise Pascal was a French mathematician who was credited with many mathematical innovations. He is perhaps most famous for what is known as Pascal’s triangle. This triangle contains many interesting number patterns. The triangle can be created by calculating the value of certain combinations.
There are other uses for Pascal’s triangle. In this lesson you will learn to expand a binomial expression to any power.
Lesson Outcomes
At the end of this lesson you will be able to
- expand powers of a binomial in a variety of ways
- identify and explain patterns in Pascal’s triangle
Lesson Questions
You will investigate the following questions:
- How do the coefficients of the terms in the expansion of (x + y)n relate to the terms of Pascal’s triangle?
- How can you expand a binomial of the form (x + y)n without multiplying all the factors?
Assessment
Your assessment may be based on a combination of the following tasks:
- completion of the Lesson 4 Assignment (Download the Lesson 4 Assignment and save it in your course folder now.)
- course folder submissions from Try This and Share activities
- additions to Glossary Terms and Formula Sheet
- work under Project Connection
1.1. Launch
Module 8: Permutations, Combinations, and the Binomial Theorem
Launch
Do you have the background knowledge and skills you need to complete this lesson successfully? Launch will help you find out.
Before beginning this lesson, you should be able to multiply polynomials.
1.2. Are You Ready?
Module 8: Permutations, Combinations, and the Binomial Theorem
Are You Ready?
Complete these questions. If you experience difficulty and need help, visit Refresher or contact your teacher.
Multiply the following polynomials.
- (−9x + 5)(−10x − 6) Answer
- (9x + 7)(6x + 4) Answer
- (−2x)(11x3 − 10x2 + 4x + 6) Answer
- (−2x2 − 4x + 11)(5x − 12) Answer
If you answered the Are You Ready? questions without difficulty, move to Discover.
If you found the Are You Ready? questions difficult, complete Refresher.
1.3. Refresher
Module 8: Permutations, Combinations, and the Binomial Theorem
Refresher
Watch the following videos about multiplying polynomials.
“Multiplying Polynomials 1”
“Multiplying Polynomials 2”
“Multiplying Polynomials 3”
Go back to the Are You Ready? section and try the questions again. If you are still having difficulty, contact your teacher.
1.4. Discover
Module 8: Permutations, Combinations, and the Binomial Theorem
Discover
Consider the binomial x + y. Suppose you want to take this binomial to the nth power: (x + y)n. What is the result of this expansion? Complete Try This 1 to begin exploring this idea.
Try This 1
- Complete the following table for (x + y)n. Arrange your expanded polynomials from the largest to the smallest exponent on x, as shown for n = 3.
n Binomial Expression
(x + y)nExpansion 0 (x + y)0 
1 (x + y)1 2 (x + y)2 3 (x + y)3 1x3 + 3x2y + 3xy2 + 1y3 4 (x + y)4 26 (x + y)26 
- Use patterns in the table to predict the number of terms in the expansion of (x + y)26.
-
Look at the exponent values on x and y.
-
What is the relationship between the x and y exponents for each term in the expanded form?

- Describe a pattern for the x exponents for a given expansion.
- Describe a relationship between the n-value and the exponents of the expansion.
-
- Use the patterns you described in question 3 to make three predictions about (x + y)26.
-
- Describe a pattern of the coefficients for a binomial expansion. You may find reviewing the image of Pascal’s triangle from Focus to be helpful.
- Can your pattern predict the coefficients for the expansion of (x + y)5? Explain.
![]() Save your responses in your course folder.
Save your responses in your course folder.
Share 1
With a partner or group, discuss the following questions based on the information from Try This 1.
- Compare the patterns you saw in questions 3 and 5.
- Do the patterns you have give enough information to determine the first term in the expansion of (x + y)26? What about the second term? What about the rest of the terms?
![]() If required, save a record of your discussion in your course folder.
If required, save a record of your discussion in your course folder.
Each term is separated by a + for this binomial expansion. So x3, 3x2y, … are separate terms.
This question may be easier if you show the exponents 0 and 1 like this: (x + y)3 = 1x3y0 + 3x2y1 + 3x1y2 + 1x0y3.
1.5. Explore
Module 8: Permutations, Combinations, and the Binomial Theorem
Explore
In Try This 1 you may have noticed that expanding a binomial power by multiplying is a very tedious task, even for relatively small exponents. There are a variety of patterns that occur when you expand the expression (x + y)n. Some of these patterns include the following:
- The number of terms in the expansion is equal to n + 1. For example, (x + y)15 will have 16 terms.
- The exponent of x and the exponent of y in each term add up to n. For example, if n = 3, each pair of exponents in a term adds up to 3.
(x + y)3 = 1x3y0 + 3x2y1 + 3x1y2 + 1x0y3 - The exponents on the x in each term in the expansion will include n, n − 1, …, 2, 1, 0. For example, if n = 4
(x + y)4 = 1x4y0 + 4x3y1 + 6x2y2 + 4x1y3 + 1x0y4 - The exponents on the y in each term in the expansion will include n, n − 1, …, 2, 1, 0. For example, if n = 4
(x + y)4 = 1x4y0 + 4x3y1 + 6x2y2 + 4x1y3 + 1x0y4
The rest of this lesson focuses on these patterns, which help to make expanding a binomial easier. The pattern for the coefficients of the terms is a bit more elusive. You will explore this pattern using Pascal’s triangle in Try This 2.
Try This 2
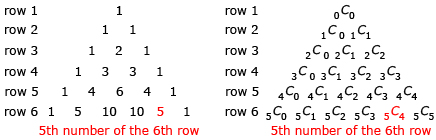
The first five rows of Pascal’s triangle are shown.
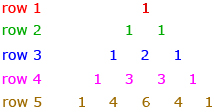
- Examine the triangle. Describe at least three patterns you see.
- Determine rows 6 and 7.
- Recall the binomial powers that you expanded in Try This 1.
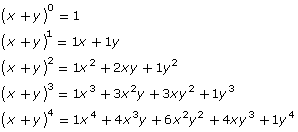
- Describe the relationship between the binomial expansions and Pascal’s triangle.
- Use Pascal’s triangle to predict the coefficients in the expansion of (x + y)6.

- Complete the expansion of (x + y)6.

- Predict the first four terms of the expansion of (x + y)10.
![]() Save your responses in your course folder.
Save your responses in your course folder.
Share 2
With a partner or group, discuss the following questions based on the patterns you determined in Try This 2.
- Compare the patterns you found in Pascal’s triangle. How did your strategy to determine the next rows compare with others?
- Compare the relationships you determined between Pascal’s triangle and binomial expansions.
- Explain why the strategy of writing out the rows of Pascal’s triangle may not be reasonable to determine the first four terms of (x + y)33.
![]() If required, save a record of your discussion in your course folder.
If required, save a record of your discussion in your course folder.
1.6. Explore 2
Module 8: Permutations, Combinations, and the Binomial Theorem
In Try This 2 you may have found that each row of Pascal’s Triangle can be determined by adding adjacent numbers in the preceding row.
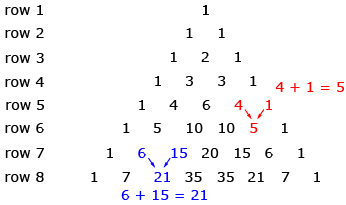
You may have noticed some of the following patterns:
- Each row is symmetrical.
- Row n has n numbers in it.
- The second number of the row is equal to n − 1.
- The sum of row n is 2n − 1.
Although Pascal’s triangle has many interesting patterns, the pattern of the triangle’s construction is most important for this lesson.
The coefficients of the binomial (x + y)n can be determined using row n + 1 of Pascal’s triangle. To determine the expansion of (x + y)7, use row 7 + 1, or row 8, of the triangle to determine the coefficients. Watch Binomial Expansion with Pascal’s Triangle to see a complete description of how to expand (x + y)7.
Self-Check 1
Complete questions 1.a., 1.b, 4, 7.a., 7.b., 11.a., 11.b., and 14 on pages 542 and 543 of the textbook. Answer
1.7. Explore 3
Module 8: Permutations, Combinations, and the Binomial Theorem
In Lesson 3 you looked at combinations. Do you think there could be a connection between combinations and Pascal’s triangle? In Try This 3 you will explore whether there is a relationship between combinations and Pascal’s triangle.
Try This 3
- Consider the following table of combinations and their values.
TABLE OF COMBINATIONS
Combination
Value
0C0
1
1C0
1
1C1
1
2C0
1
2C1
2
2C2
1
3C0
1
3C1
3
3C2
3
3C3
1
4C0
1
4C1
4
4C2
6
4C3
4
4C4
1
- Describe a relationship between the table of combinations and Pascal’s triangle.

- Try your relationship for row 7.
- Use your relationship to predict the 1st, 2nd, 3rd, and 4th numbers of row 34 of Pascal’s triangle.
- Determine the first four terms of (x + y)33.

- Describe a relationship between the table of combinations and Pascal’s triangle.
- Explain a general method that can be used to predict the terms of the expansion of (x + y)n.
![]() Save your responses in your course folder.
Save your responses in your course folder.
Share 3
With a partner or group, discuss the following question based on the information in Try This 3.
Compare the strategies you thought of to determine the terms of the expansion of (x + y)n.
![]() If required, save a record of your discussion in your course folder.
If required, save a record of your discussion in your course folder.
1.8. Explore 4
Module 8: Permutations, Combinations, and the Binomial Theorem
The value of an entry in Pascal’s triangle can be determined using combinations. nCk is equal to the value of the (k + 1)th number of the (n + 1)th row. For example, in 5C4, k = 4 and n = 5. So, you need to look to the (4 + 1)th, or 5th, number in the (5 + 1)th, or 6th, row. So, 5C4 = 5.
So far you have seen a pattern for determining
- the exponents of a binomial expansion
- a method for determining the coefficients of a binomial expansion using Pascal’s triangle
- a method of determining the values of Pascal’s triangle using combinations
Putting these together results in the binomial theorem, which can be used to determine each term of a binomial expansion. You may have already determined your own version of the binomial theorem in Try This 3. One common way of writing the theorem is as follows:
(x + y)n = nC0(x)n(y)0 + nC1(x)n−1(y)1 + nC2(x)n−2(y)2 +![]() + nCn−1(x)1(y)n−1 + nCn(x)0(y)n
+ nCn−1(x)1(y)n−1 + nCn(x)0(y)n
Try to match the terms of this expression to the expression you began to expand in Try This 3.
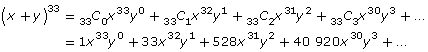
If you are interested in a particular term, the following formula can be used:
tk+1 = nCk(x)n−k(y)k
Watch Term of a Binomial Expansion to see how this formula is used to determine the sixth term of (3f − g2)14.
If you would like to see another example of how the binomial theorem can be used, read “Example 2” on page 540 of the textbook. Otherwise, continue to Self-Check 2.
Self-Check 2
- Complete “Your Turn” from “Example 2” on page 541 of the textbook. Answer
- Complete questions 3.b., 11.c., 12.a., 12.b., 17.a., and 17.d. on pages 542 to 543 of the textbook. Answer
Add the following terms to your copy of Glossary Terms:
- Pascal’s triangle
- binomial theorem
Add the following formulas to your copy of Formula Sheet:
- binomial theorem:
(x + y)n = nC0(x)n(y)0 + nC1(x)n−1(y)1 + nC2(x)n−2(y)2 + + nCn−1(x)1(y)n−1 + nCn(x)0(y)n
+ nCn−1(x)1(y)n−1 + nCn(x)0(y)n - general term in the expansion of (x + y)n: tk + 1 = nCk (x)n − k (y)k
1.9. Connect
Module 8: Permutations, Combinations, and the Binomial Theorem
Complete the Lesson 4 Assignment that you saved in your course folder at the beginning of this lesson.
![]() Save your responses in your course folder.
Save your responses in your course folder.
Project Connection
Go to Module 8 Project: Creating the Ultimate Password. Complete Activity 4: Tricky Passwords. Also complete the Conclusion.
![]() Save your responses in your course folder. When you are finished, submit the entire project to your teacher.
Save your responses in your course folder. When you are finished, submit the entire project to your teacher.
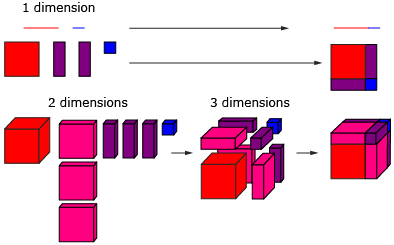
Going Beyond
The binomial theorem can be explained geometrically up to a power of 3. Explain how the following is representative of the binomial theorem. If you need help, open Going Beyond Hint.
![]() Save your responses in your course folder.
Save your responses in your course folder.
1.10. Lesson 4 Summary
Module 8: Permutations, Combinations, and the Binomial Theorem
Lesson 4 Summary
Expanding a binomial by multiplying is a very tedious process for any exponent larger than 3. It is possible to use patterns to help simplify this process. The exponents of the expansion follow an ascending and descending pattern, while the coefficients of the expansion can be found using Pascal’s triangle.
Determining the values of Pascal’s triangle for large exponents would take a long time, so combinations are used to determine entries of Pascal’s triangle to simplify this process. The generalized result is the binomial theorem:
![]()
Any term of the expansion can be determined using the formula tk + 1 = nCk (x)n − k (y)k.