Lesson 1
| Site: | MoodleHUB.ca 🍁 |
| Course: | Math 30-1 SS |
| Book: | Lesson 1 |
| Printed by: | Guest user |
| Date: | Tuesday, 9 December 2025, 11:16 PM |
Description
Created by IMSreader
1. Lesson 1
Module 4: Foundations of Trigonometry
Lesson 1: Radians and Degrees in Standard Position
Focus

Hemera/Thinkstock
When asked to measure angles in circles or triangles in previous math courses, you likely gave your response using the unit of degrees. Why degrees? Did you know that there are other units you can use to measure angles? Why not use radians, gradients, or arc minutes?
Do you know why there are 360° in a circle? One theory gives credit to the ancient Babylonians. The ancient Babylonians, who lived from approximately 2000 BC, used a sexagesimal (base-60) number system instead of the base-10 number system used today.
Another theory is that the ancient Babylonians believed the sun revolved around Earth in approximately 360 days, and that there were 60 days in each season. Or maybe 360 was chosen because it is so easily divided by 24 numbers.
In this lesson you will learn about measuring angles in a unit other than degrees.
Lesson Outcomes
At the end of this lesson you will be able to
- define radian measure
- determine a relationship between degrees and radians
- determine a method for converting between degrees and radians and between radians and degrees
- sketch angles given in degrees and radians, positive and negative, in standard position
Lesson Questions
You will investigate the following question:
- What relationship exists between degree and radian measures?
Assessment
Your assessment may be based on a combination of the following tasks:
- completion of the Lesson 1 Assignment (Download the Lesson 1 Assignment and save it in your course folder now.)
- course folder submissions from Try This and Share activities
- additions to Glossary Terms
- work under Project Connection
Self-Check activities are for your own use. You can compare your answers to suggested answers to see if you are on track. If you have difficulty with concepts or calculations, contact your teacher.
Remember that the questions and activities you will encounter provide you with the practice and feedback you need to successfully complete this course. You should complete all questions and place your responses in your course folder. Your teacher may wish to view your work to check on your progress and to see if you need help.
Time
Each lesson in Mathematics 30-1 Learn EveryWare is designed to be completed in approximately two hours. You may find that you require more or less time to complete individual lessons. It is important that you progress at your own pace, based on your individual learning requirements.
This time estimation does not include time required to complete Going Beyond activities or the Module Project.
1.1. Launch
Module 4: Foundations of TrigonometryFoundations of Trigonometry
Launch
Do you have the background knowledge and skills you need to complete this lesson successfully? Launch will help you find out.
Before beginning this lesson you should be able to
- draw and identify angles in standard position from 0° to 360°
- understand an arc subtended by a central angle
1.2. Are You Ready?
Module 4: Foundations of Trigonometry
Are You Ready?
Complete these questions. If you experience difficulty and need help, visit Refresher or contact your teacher.
- Draw the following angles in standard position.
- In which quadrant does the terminal arm lie for each of the following angles drawn in standard position?
- Draw a diagram of a circle with a central angle of approximately 60°, and label the arc subtended by the central angle. Answer
If you answered the Are You Ready? questions without difficulty, move to Discover.
If you found the Are You Ready? questions difficult, complete Refresher.
1.3. Refresher
Module 4: Foundations of Trigonometry
Refresher
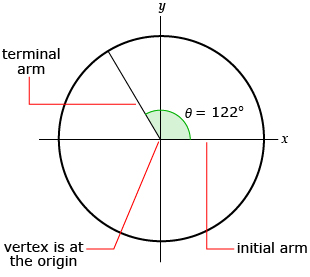
Recall that angles in standard position
- have their vertex at the origin (point (0, 0) on the Cartesian plane)
- are formed by an initial arm on the positive x-axis and a terminal arm
- are “swept out” in a counterclockwise direction from the initial arm to the terminal arm
Open Cartesian Plane. Review the four quadrants in the Cartesian plane.
Review the relationships between the terms to subtend, central angle, and arc in Subtend.
Go back to the Are You Ready? section and try the questions again. If you are still having difficulty, contact your teacher.
1.4. Discover
Module 4: Foundations of Trigonometry
Discover
Try This 1
Step 1: Read through “Investigate Angle Measure” on pages 166 and 167 of the textbook.
Step 2: Open “Angle Measure Investigation: Khadija and Steve’s Work.” Watch Khadija and Steve complete the investigation.
Share 1
Share your observations and responses to Try This 1 with a classmate or group. In your sharing session, discuss the following questions.
- How many times did the length of the radius fit around the circumference of Khadija’s circle?
- How many times did the length of the radius fit around the circumference of Steve’s circle?
- How did Khadija’s central angle compare to Steve’s central angle? How many times do you think the length of the radius of any circle would fit around the circumference?
![]() If required, place a summary of your discussion in your course folder.
If required, place a summary of your discussion in your course folder.
1.5. Explore
Module 4: Foundations of Trigonometry
Explore
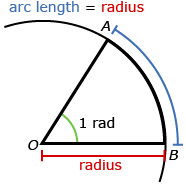
In Try This 1 you created a central angle where the radius, AO, of the circle is the same as the length of the subtended arc, AB. This situation defines radian measure. The measure of ∠AOB is 1 rad (radian).
You may have determined that the radius of the circle would fit about 6 times around the circumference of a circle. This would mean that one full rotation, which is 360°, would be the same as about 6 rad. In Try This 2 you will try to find a more precise value for one full rotation of a circle measured in radians.
Try This 2
You will test your new understanding of 1 rad by investigating whether the radius of a circle changes the measure of the central angle. You will then explore the relationship between radians and degrees.
Step 1: Open Angles in Degrees and Radians.
Step 2: Slide the angle slider to change the angle to 60°. Use the arrow keys on your keyboard to change the angle by 1° at a time. Note where 1 rad is positioned.
Step 3: Slide the radius slider to change the radius to a larger value and then to a smaller value. Did the radian measure change? Why do you think this happens? ![]()
- Use Angles in Degrees and Radians to complete a chart similar to the one that follows. You will notice that the radian measure is given in red as an exact measure in terms of π first and is then rounded to three decimal places.
Degree Portion of Whole Circle Radian Measure
(in terms of π)
Radian Measure
(round to three decimal places)
Sketch or Screen Capture 360° 1 
180° 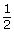

90° 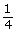

45° 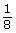

−360° −1 
−180° 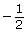

−90° 

−45° 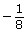

- If the angle is positive, in which direction does the terminal arm rotate?

-
If the angle is negative, in which direction does the terminal arm rotate?

- What relationship can you see between degrees and radians? Describe this relationship in terms of π rad.
Use the relationship you found in question 4 to answer the following questions.
- How are degrees related to radians?
- Complete a chart similar to the one that follows. Leave radians as exact measures. You can check your answers when you are finished by using Angles in Degrees and Radians.
Degree Radian
(exact value, fraction of π)
Sketch Quadrant 30° 
60° 
−120° 
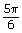

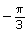

![]() Save your responses in your course folder.
Save your responses in your course folder.
Share 2
With a partner or in a group, discuss the following questions:
- How did you determine the answer to questions 5 and 6?
- Are your methods for changing degrees to radians and radians to degrees the same or different than your partner’s methods?
![]() If required, save a record of your discussion in your course folder.
If required, save a record of your discussion in your course folder.
1.6. Explore 2
Module 4: Foundations of Trigonometry
In Try This 1 you explored how a radian is defined by looking at both the radius and the arc length of a circle. In Try This 2 you made the connection that one rotation of a circle is 360°, and this is equal to 2π rad. You know that
- 360° = 2π rad
- 180° = π rad
In this next example you will see how the relationship between degrees and radians can be used to convert between radians and degrees.
When an angle measurement is given and there are no units written after the measurement, you can assume the units are in radians. When writing an angle measurement in degrees, the degree symbol must be included to indicate the measurement is in degrees. For example,
- 75° indicates 75 degrees
- 110 indicates 110 radians (rad)
Read “Example 1” on pages 168 to 169 of the textbook. Think about the following as you read:
- The angle is drawn in standard position.
- Three different methods are used to find solutions: unitary method, proportion method, and unit analysis. Which method do you prefer?
Watch “Radians and degrees” for a summary of converting between degrees and radians. If you feel comfortable converting between degrees and radians, you can skip the video and go to Self-Check 1.
Self-Check 1
![]()
- Complete “Your Turn” on page 169 of the textbook. Answer
- Complete questions 2.a., 2.b., 2.c., 4.a., 4.b., 4.c., 4.e., 6.a., 6.b., and 6.e. on page 175 of the textbook. Answer
- Complete question C4 on page 179 of the textbook. Answer

Pixland/Thinkstock
Angles can be measured in many different units. In the military it is sometimes necessary to measure very small angles when using a compass. Mils, or angular mils, are a unit the British Army uses to measure angles. Under this system, the circle of the compass is divided into 6400 gradations called mils.
Each quadrant of the circle, which is 90°, is equal to 1600 mils. This means that north is at 0/6400 mils, east is at 1600 mils, south is at 3200 mils, and west is at 4800 mils. Because the divisions are smaller, readings can be more accurate.1
Add radian to your copy of Mathematics 30-1 Glossary Terms.
For help defining the glossary term, you can refer to Radian Measure or to “Link the Ideas” on page 167 of the textbook for help.
1 Source: Adapted from ArmyCadetForce.net
1.7. Connect
Module 4: Foundations of Trigonometry
Complete the Lesson 1 Assignment that you saved in your course folder at the beginning of the lesson. Show work to support your answers.
![]() Save your responses in your course folder.
Save your responses in your course folder.
Project Connection
You are ready to start working on Module 4 Project: The Ferris Wheel. Go to the Module 4 Project and read over all project requirements. Become familiar with what you will be doing and how you will be assessed.
Complete Part 1: Activity 1 of Module 4 Project: The Ferris Wheel.
![]() Save your responses in your course folder.
Save your responses in your course folder.
1.8. Lesson 1 Summary
Module 4: Foundations of Trigonometry
Lesson 1 Summary

Comstock/Thinkstock
In this lesson you learned that angles can be described using different measures and units. You focused on the relationship between degrees and radians. In Try This 1 you discovered how to describe an angle measure of 1 rad. You used the ratio of the radius and arc length to determine measurements in radians.
In Try This 2, Angles in Degrees and Radians helped you find the relationship 360° = 2π rad. Understanding this relationship allows you to convert between radians and degrees using any method.
You were able to visualize the following:
- Angles in standard position are positive when the terminal arm rotates counterclockwise.
- Angles in standard position are negative when the terminal arm rotates clockwise.
You applied this understanding in Module 4 Project: The Ferris Wheel to describe the direction of motion of the Ferris wheel.
Throughout the rest of Module 4 you will continue to look at objects that move in circular paths, such as amusement park rides. In Lesson 2 you will use the relationship between radians and degrees to explain the distance travelled by an object moving in a circular path.