Lesson 5
| Site: | MoodleHUB.ca 🍁 |
| Course: | Math 30-1 SS |
| Book: | Lesson 5 |
| Printed by: | Guest user |
| Date: | Tuesday, 9 December 2025, 11:13 PM |
Description
Created by IMSreader
1. Lesson 5
Module 4: Foundations of Trigonometry
Lesson 5: Trigonometric Equations
Focus

iStockphoto/Thinkstock
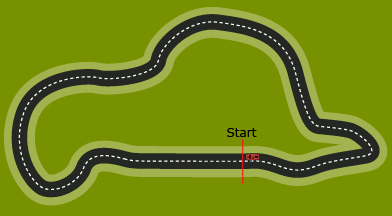
The Circuit Gilles Villeneuve is a motor-racing circuit in Montréal that hosts the Canadian Grand Prix car race. During this Formula 1 race, cars reach speeds of 360 km/h while traveling 70 laps around the 4.4-km loop.
Suppose you wanted to answer this question: How far has a car travelled when it crosses the finish line? You might answer 4.4 km, 8.8 km, or something else. How many answers are there? Is there a way to represent all of these answers without writing each one out?
In this lesson you will learn to solve some first- and second-degree trigonometric equations. You will also learn how to represent an infinite number of solutions as a general solution.
Lesson Outcomes
At the end of this lesson you will be able to
- determine the measure of angles that produce a given trigonometric ratio
- algebraically determine the solution to a first- and second-degree trigonometric equation over a restricted domain
- verify a solution to a trigonometric equation
- determine a general solution to a trigonometric equation
- solve problems using trigonometric ratios
Lesson Questions
You will investigate the following questions:
- How can trigonometric equations be solved?
- How is a specific solution for a trigonometric equation related to the general solution?
Assessment
Your assessment may be based on a combination of the following tasks:
- completion of the Lesson 5 Assignment (Download the Lesson 5 Assignment and save it in your course folder now.)
- course folder submissions from Try This and Share activities
- additions to Glossary Terms
- work under Project Connection
1.1. Launch
Module 4: Foundations of Trigonometry
Launch
Do you have the background knowledge and skills you need to complete this lesson successfully? Launch will help you find out.
Before beginning this lesson you should be able to
- solve a quadratic equation by factoring
- determine angles between 0° and 360° when given a trigonometric ratio
1.2. Are You Ready?
Module 4: Foundations of Trigonometry
Are You Ready?
Complete these questions. If you experience difficulty and need help, visit Refresher or contact your teacher.
- Completely factor each expression.
- Solve for x in the following equations.
- Determine all the values of θ where
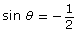 in the interval 0° ≤ θ < 360°. Answer
in the interval 0° ≤ θ < 360°. Answer
If you answered the Are You Ready? questions without difficulty, move to Discover.
If you found the Are You Ready? questions difficult, complete Refresher.
1.3. Refresher
Module 4: Foundations of Trigonometry
Refresher
Review Common Factor.
Review Modelling the Factorization of ax2 + bx + c.
Review Solving Quadratic Equations: Factoring. Go into Tutorial and choose Factoring to Solve Quadratic Equations.
Work through the following examples of how to determine angles between 0° and 360° when given a trigonometric ratio:
- Example 1: Equations of the Form cos θ = k, Where −1 ≤ k ≤ 1
- Example 2: Equations of the Form sin θ = k, Where −1 ≤ k ≤ 1


Go back to the Are You Ready? section and try the questions again. If you are still having difficulty, contact your teacher.
1.4. Discover
Module 4: Foundations of Trigonometry
Discover
Try This 1
Take out the unit circle you created in Lesson 3: Try This 4. Use the circle to help determine the values of θ that make the expression ![]() true.
true.
- How many solutions are there to the equation
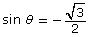 on the unit circle?
on the unit circle? 
- Determine three coterminal angles for one of the solutions to
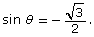 Are these angles also solutions to the equation? Explain how you know these angles are solutions.
Are these angles also solutions to the equation? Explain how you know these angles are solutions.
![]() Save your responses in your course folder.
Save your responses in your course folder.
Share 1
Discuss your responses to Try This 1 with a partner or group. Answer the following questions.
- How are the coterminal angles related to the original solutions of
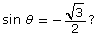
- How many different solutions are there for the equation
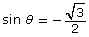 in the real numbers?
in the real numbers?
![]() If required, save a record of your discussion in your course folder.
If required, save a record of your discussion in your course folder.
1.5. Explore
Module 4: Foundations of Trigonometry
Explore
A trigonometric equation is an equation that includes the trigonometric ratio of a variable. Note these examples:
- 3 tan x − 7 = 5 is a trigonometric equation because you need to find the tangent ratio for x.
- x tan 7 − 5 = 3 is not a trigonometric equation because you are finding the tangent ratio of 7, not the tangent of a variable.
In Try This 1 you began to look at the solutions to a trigonometric equation. You may have found that a trigonometric equation will often have more than one solution between 0 and 2π and may have unlimited solutions in the real numbers.
The next activity leads you through solving a trigonometric equation that has a reciprocal trigonometric ratio and a domain in radians.
Try This 2
To calculate a reference angle with your calculator for a trigonometric equation, you can enter the ratio and use the sin−1 , cos−1, or tan−1 button.
Example
tan θ = 0.50, so tan−1 0.50 = 25.560 511 8…°
θ ≈ 25.6° (Calculator is in degree mode.)
tan θ = 0.50, so tan−1 0.50 = 0.463 647 609… rad.
θ ≈ 0.46 (Calculator is in radian mode.)
Complete Solving Trigonometric Equations 1. Pay attention to how a reference angle is used to solve the equation.
The notation sin−1x refers to the inverse of the sine function. The notation is not a reciprocal; ![]() but
but ![]()
To see another example of determining an angle given a ratio, read “Example 4” on pages 198 and 199 of the textbook.
Self-Check 1
Complete questions 10.a., 10.c., and 11.d. on page 202 of the textbook. Answer
1.6. Explore 2
Module 4: Foundations of Trigonometry
Many trigonometric equations are more complex than the ones seen so far. Some of these can be solved using many of the algebraic strategies you learned in previous courses. The key is to isolate the trigonometric term. This is often done by collecting like terms, as in the following example.
Read “Example 1” on pages 207 and 208 of the textbook.
Share 2 is based on “Example 1.”
Share 2
With a partner or group, discuss how solving 5 sin θ + 2 = 1 + 3 sin θ compares to solving the equation 5x + 2 = 1 + 3x.
![]() If required, save a record of your discussion in your course folder.
If required, save a record of your discussion in your course folder.
Self-Check 2
Complete questions 1.a., 1.c., 3.a., 3.b., 4.c., and 4.e. on page 211 of the textbook. Answer
So far you have solved first-degree trigonometric equations. Next you will explore how to solve a second-degree trigonometric equation by factoring. A second-degree trigonometric equation includes a trigonometric ratio squared, such as (sin x)2 = 0.45. Often (sin x)2 is written as sin2x.
The solutions to a trigonometric equation can be checked by substitution, just like other equations. To substitute, replace the variable with a solution and check that the equation is true.
Take a look at Solving Trigonometric Equations 2. Notice the similarities between solving a trigonometric equation by factoring and solving a quadratic equation by factoring.
Self-Check 3
![]()
1.7. Explore 3
Module 4: Foundations of Trigonometry
Try This 3
Coterminal Angles Between −720° and 1080° |
|
| Solution 1: θ = ______ | |
| Solution 2: θ = ______ |
- Solve the equation 2 cos θ + 1 = 0, 0° ≤ θ < 360°. Record the two solutions in a table similar to the table shown.
- Use Coterminal Angles 2 to find all the coterminal angles for each solution from −720° to 1080°, and complete the table.

-
Replace θ from the original equation with one of the coterminal angles you found in question 2. Simplify. What do you notice? Is this true for all of the coterminal angles?
- Use your results from question 3 to determine all solutions to 2 cos θ + 1 = 0, −720° ≤ θ < 1080°.
-
How many solutions will there be to 2 cos θ + 1 = 0 if the domain is the real numbers instead of −720° ≤ θ < 1080°?
-
How could you represent all the solutions over the real numbers?
- Repeat questions 1 to 6 using the equation tan θ − 1 = 0 with radians instead of degrees.
![]() Save your responses in your course folder.
Save your responses in your course folder.
Share 3
With a partner or group, discuss the following questions based on your results from Try This 3.
- How were you able to represent all the solutions to the two equations over the real numbers? Were your methods different?
- Why could the solutions to the tangent equation be shown using one expression while the solutions to the cosine equation required two expressions?
![]() If required, save a record of your discussion in your course folder.
If required, save a record of your discussion in your course folder.
1.8. Explore 4
Module 4: Foundations of Trigonometry
In Try This 3 you explored what is called the general solution to an equation. A general solution is an expression that represents all solutions when the domain is unrestricted. A common way to write the general solution to the equation 2 cos θ + 1 = 0 is as follows:
θ = 120° + 360°n, n ∈ I and θ = 240° + 360°n, n ∈ I
Together, these represent all the solutions to 2 cos θ + 1 = 0.
The general solution to tan θ − 1 = 0 can be written as ![]() + nπ, n ∈ I.
+ nπ, n ∈ I.
| Equation | The General Solution | Angles the General Solution Refers To |
| 2 cos θ + 1 = 0 | θ = 120° + 360°n, n ∈ I | …−600°, −240°, 120°, 480°, 840°, 1200°… |
| θ = 240° + 360°n, n ∈ I | …−480°, −120°, 240°, 600°, 960°, 1320°… | |
| tan θ − 1 = 0 |
Watch and listen to How to Read a Solution.
The number of solutions contained in one rotation of the unit circle is often the number of expressions required in the general solution. An exception to this guideline occurs when solutions are one-half of a rotation apart, as shown in the previous tangent equation.
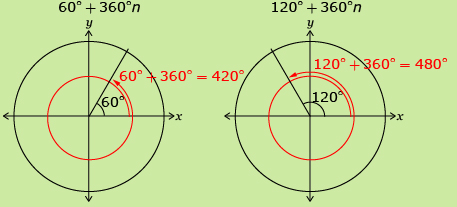
The solution to 2 cos θ + 1 = 0 requires two expressions. There is one expression for each unique point on the unit circle.
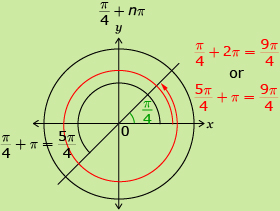
The solution to tan θ − 1 = 0 can be written as ![]() and
and ![]() These two solutions are one-half of a rotation, or π, apart so they can be combined to
These two solutions are one-half of a rotation, or π, apart so they can be combined to ![]() In degrees, this is 45° + 180°n, n ∈ I.
In degrees, this is 45° + 180°n, n ∈ I.
Read “Example 3” on pages 209 and 210 of the textbook. Pay attention to the relationship between the solutions over a particular domain and the general solution.
Self-Check 4
Complete questions 2, 5.f., 9, 10, and 14 on pages 211 and 212 of the textbook. Answer
- trigonometric equation
- general solution
1.9. Connect
Module 4: Foundations of Trigonometry
Complete the Lesson 5 Assignment that you saved in your course folder at the beginning of the lesson. Show work to support your answers.
![]() Save your work in your course folder.
Save your work in your course folder.
Project Connection
You are now ready to complete the next step of Module 4 Project: The Ferris Wheel. Complete Part 1: Activity 4.
![]() Save your work in your course folder.
Save your work in your course folder.
1.10. Lesson 5 Summary
Module 4: Foundations of Trigonometry
Lesson 5 Summary

F1online/Thinkstock
In previous math courses you explored how to solve trigonometric ratios from 0° to 360°. In this lesson you solved equations using radians and reciprocal trigonometric ratios for all angles.
You also learned to solve more complex trigonometric equations. You used skills learned previously to isolate the trigonometric term (e.g., sin θ, cos θ, tan θ). You then used the unit circle to obtain exact values of the angle. Your calculator can also be used to give approximate values. Read questions carefully to know what is required.
A general solution gives all possible solutions for an equation. To determine a general solution, find the solutions in one positive rotation and then determine other solutions using coterminal angles. A general solution may be written in the form θ = ___ + ___ nπ, n ∈ I. More than one expression is often required to express a general solution. In Lesson 6 you will begin to explore visual representations of trigonometric functions.
In upcoming lessons you will learn to apply this new understanding to solve problems that involve cyclic behaviour, such as amusement park rides.