Lesson 1
| Site: | MoodleHUB.ca 🍁 |
| Course: | Math 30-1 SS |
| Book: | Lesson 1 |
| Printed by: | Guest user |
| Date: | Tuesday, 9 December 2025, 11:16 PM |
Description
Created by IMSreader
1. Lesson 1
Module 2: Radical Functions
Lesson 1: Radical Functions and Transformations
Focus

iStockphoto/Thinkstock
Police officers use mathematics to analyze car accident scenes. Investigators are able to determine what likely happened without even seeing the actual accident. To determine the vehicle’s speed before the collision, investigators may use the formula ![]() where S is the speed of the vehicle, L is the length of the skid marks, and f is the coefficient of friction (determined by the road surface). By looking at the formula, can you describe the relationship between speed and the length of skid marks? Would a graph of this function help you to more easily see the relationship?
where S is the speed of the vehicle, L is the length of the skid marks, and f is the coefficient of friction (determined by the road surface). By looking at the formula, can you describe the relationship between speed and the length of skid marks? Would a graph of this function help you to more easily see the relationship?
In Lesson 1 you will look at graphing functions that include radical signs.
Lesson Outcomes
At the end of this lesson, you will be able to
- sketch the graph of radical functions
- state the domain and range of radical functions
- apply transformations to radical functions
Lesson Questions
You will investigate the following questions:
- How can radical functions be graphed?
- How are graphs of radical functions used to analyze real-life situations?
Assessment
Your assessment may be based on a combination of the following tasks:
- completion of the Lesson 1 Assignment (Download the Lesson 1 Assignment and save it in your course folder now.)
- course folder submissions from Try This and Share activities
- additions to Glossary Terms and Formula Sheet
- work under Project Connection
Self-Check activities are for your own use. You can compare your answers to suggested answers to see if you are on track. If you have difficulty with concepts or calculations, contact your teacher.
Remember that the questions and activities you will encounter provide you with the practice and feedback you need to successfully complete this course. You should complete all questions and place your responses in your course folder. Your teacher may wish to view your work to check on your progress and to see if you need help.
Time
Each lesson in Mathematics 30-1 Learn EveryWare is designed to be completed in approximately two hours. You may find that you require more or less time to complete individual lessons. It is important that you progress at your own pace, based on your individual learning requirements.
This time estimation does not include time required to complete Going Beyond activities or the Module Project.
Materials and Equipment
- graph paper
1.1. Launch
Module 2: Radical Functions
Launch
Do you have the background knowledge and skills you need to complete this lesson successfully? Launch will help you find out.
Before beginning this lesson, you should be able to
- identify restrictions on variables in radical expressions
- determine the value of square roots
- determine the inverse of a function
1.2. Are You Ready?
Module 2: Radical Functions
Are You Ready?
Complete these questions. If you experience difficulty and need help, visit Refresher or contact your teacher.
- Identify any restrictions on the variable in the following expressions.
- Determine the value of the following:
- Determine the equation of the inverse function of the function f(x) = 8x2, x ≥ 0. Answer
If you answered the Are You Ready? questions without difficulty, move to Discover.
If you found the Are You Ready? questions difficult, complete Refresher.
1.3. Refresher
Module 2: Radical Functions
Refresher
Go to Radical at the Mathematics Glossary website to review the definition of radical.
The video titled “Domain of a Function” provides a review of restrictions on the variable in radical expressions.
For a review of square roots of value, view the video titled “Understanding Square Roots.”
The video “Function Inverses Example 2” provides a review of the inverse of a quadratic function.
Go back to the Are You Ready? section and try the questions again. If you are still having difficulty, contact your teacher.
1.4. Discover
Module 2: Radical Functions
Discover
Air resistance causes objects falling to Earth to fall at different rates. If air resistance is removed, all objects drop at the same rate. The video “The Hammer and Feather” shows two objects falling in a vacuum (i.e., there is no air resistance).
Try This 1

© justinkendra/20827683/Fotolia
For objects falling near the surface of Earth, the function d = 5t2 approximately models the time, t, in seconds, for an object to fall a distance, d, in metres, if the resistance caused by air can be ignored.
-
- Identify any restrictions on the domain of the function d = 5t2. Why are these restrictions necessary?

- What is the range of the function?
- Create and complete a table similar to the following for the function d = 5t2.
t d - Create a graph showing the distance fallen as a function of time.
- Identify any restrictions on the domain of the function d = 5t2. Why are these restrictions necessary?
- Determine the equation of the inverse function of d = 5t2.
- Create and complete a table of values similar to the following, and then graph the inverse function.1
t d
![]() Save your responses in your course folder.
Save your responses in your course folder.
Share 1
With a partner or in a group, compare and describe the original function and the inverse function in terms of domain, range, and shape of graph.
![]() If required, save a record of your discussion in your course folder.
If required, save a record of your discussion in your course folder.
1 Adapted from Pre-Calculus 12. Whitby, ON: McGraw-Hill Ryerson, 2011. Reproduced with permission.
1.5. Explore
Module 2: Radical Functions
Explore
The inverse function from Try This 1 was ![]() this is a radical function.
this is a radical function.
Read “Link the Ideas” on page 63 of the textbook for a description of radical functions.
In Try This 2 you will see how radical functions can be represented using tables of values and graphs.
Try This 2
Graph ![]()
- What restrictions are on x in the function
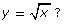
- Make a table of values. Are some values of x easier to use than others? Carefully choose the values of x and record these values in a table like the following. Calculate the y-values and record them.
x y 0 0 - Use Grid Paper Template, which is also available in the Toolkit. Sketch the graph.
- State the domain and range of the graph. Why do you think the domain is restricted?
![]() Save your responses in your course folder.
Save your responses in your course folder.
1.6. Explore 2
Module 2: Radical Functions
In Try This 2 you graphed the simplest radical function possible: ![]() Did you notice the distinct shape that you graphed? You may remember this shape from Try This 1 in Discover. You have now seen two radical functions with this distinct shape. This shape is sometimes describes as one-half of a parabola opening to the right. The domain of the function is {x|x ≥ 0, y ∈ R} because you cannot take the square root of a negative number. The range of the function is {y|y ≥ 0, y ∈ R}.
Did you notice the distinct shape that you graphed? You may remember this shape from Try This 1 in Discover. You have now seen two radical functions with this distinct shape. This shape is sometimes describes as one-half of a parabola opening to the right. The domain of the function is {x|x ≥ 0, y ∈ R} because you cannot take the square root of a negative number. The range of the function is {y|y ≥ 0, y ∈ R}.
Radical functions can be much more complex than the function you graphed in Try This 2. The general form of a radical function can be written as ![]() Do you see the similarities in this form to the general form for functions used in Module 1?
Do you see the similarities in this form to the general form for functions used in Module 1?
In Try This 3 you will investigate how the graph of radical functions changes in response to changes in the parameters a, h, and k of the general form of the function.
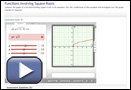
Try This 3
Open “Functions Involving Square Roots.”
Select the “Show domain” and “Show range” boxes in the gizmo.
This gizmo begins with a graph of ![]() Check that your graph, the domain, and the range from Try This 2 match this graph.
Check that your graph, the domain, and the range from Try This 2 match this graph.
- Use the slider to change the value of a, and record your answers in a chart like the following.

a-value
Function
Domain
Range
Transformation of Graph and State the Stretch Factor
Sketch or Image
1 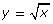
{x|x ≥ 0, x ∈ R}
{y|y ≥ 0, y ∈ R}
none 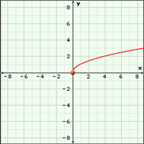
Screenshot reprinted with
permission of ExploreLearning.Positive value:
________
Negative value:
________
-
Set the a-value back to 1. Use the slider and change the value of h, and record your answers in a chart like the following.

h-value
Function
Domain
Range
Transformation of Graph and State the Value of the Translation
Sketch or Image
0 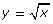
{x|x ≥ 0, x ∈ R}
{y|y ≥ 0, y ∈ R}
none 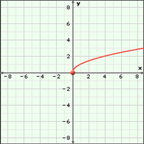
Screenshot reprinted with
permission of ExploreLearning.Positive value:
________Negative value:
________ - Set the h-value back to zero. Use the slider, change the value of k, and record your answers in a chart like the following.
k-value
Function
Domain
Range
Transformation of Graph and State the Value of the Translation
Sketch or Image
0 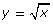
{x|x ≥ 0, x ∈ R}
{y|y ≥ 0, y ∈ R}
none 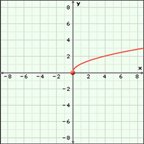
Screenshot reprinted with
permission of ExploreLearning.Positive value:
________Negative value:
________
Open Multiple Transformations. Click on “Quadratic” to deselect it, and click on “Square root” to select this type of function.

- Change the a, b, h, and k sliders to explore what happens to the graph when these values are changed. In a chart like the following, summarize how the parameters a, b, h, and k transform the graph given in the general form
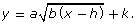
Parameter Value > 0 Value < 0 a b h k
![]() Save your responses in your course folder.
Save your responses in your course folder.
1.7. Explore 3
Module 2: Radical Functions
In Try This 3 you may have noticed that the parameters a, b, h, and k from the general form ![]() affect the graph of the radical equation in the following ways.
affect the graph of the radical equation in the following ways.
| Parameter | Value > 0 | Value < 0 |
| a | Vertical stretch of graph of |
Vertical stretch of graph of |
| b | Horizontal stretch of graph of |
Horizontal stretch of graph of |
| h | Graph of |
Graph of |
| k | Graph of |
Graph of |
Self-Check 1
- Complete the four questions at the bottom of “Functions Involving Square Roots.” Check your answers.
![]()
- Complete questions 2.a., 2.c., and 3 on page 72 of the textbook. Answers
Now that you have seen how radical functions can be transformed by different parameters, you will use this understanding to graph transformed radical functions. The following animated examples show two different methods that can be used to graph radical functions using transformations. Do you prefer one of the methods?
Method 1: Transform the Graph Directly
Go to Graphing Radical Functions by Transforming the Graph.
Method 2: Map Individual Points
Go to Graphing Radical Functions by Mapping Points.
If you would like to review some more examples about how the two methods are used to graph radical functions, read “Example 2” on pages 65 to 67 of the textbook.
Self-Check 2
1.8. Explore 4
Module 2: Radical Functions
Why did the applet used in Try This 3 use the form ![]() and not the form
and not the form ![]()
Look at an example of two radical functions to help understand how the a and b parameters can both be used to describe stretches of radical functions.
Try This 4
You will look at the graphs of the function ![]() and
and ![]() to see how these two functions are related.
to see how these two functions are related.
- Describe how to transform the graph of
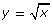 to produce the graph of the function
to produce the graph of the function 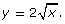
- Describe how to transform the graph of
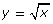 to produce the graph of the function
to produce the graph of the function 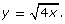
- Graph each of the two functions
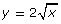 and
and 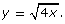 Use a graphing calculator or graphing program; or graph them by hand.
Use a graphing calculator or graphing program; or graph them by hand. - Are the two functions
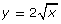 and
and 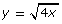 equivalent? Explain your reasoning.
equivalent? Explain your reasoning.
![]() Save your work in your course folder.
Save your work in your course folder.
1.9. Explore 5
Module 2: Radical Functions
Radical functions can be written as having a vertical stretch or a horizontal stretch. In Try This 4 you looked at the radical functions ![]() and
and ![]() and discovered that the graphs of these two functions are the same. When you look at the functions, you can see how the second function can be rearranged to be the same as the first function.
and discovered that the graphs of these two functions are the same. When you look at the functions, you can see how the second function can be rearranged to be the same as the first function.
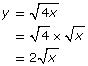
You can compare these functions to the function ![]() and describe the function
and describe the function ![]() as having a vertical stretch by a factor of 2.
as having a vertical stretch by a factor of 2.
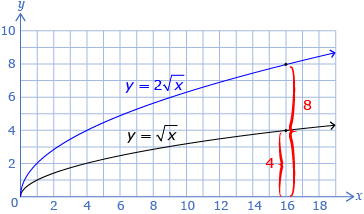
When you compare ![]() to
to ![]() you can describe the transformation as a horizontal stretch by a factor of
you can describe the transformation as a horizontal stretch by a factor of ![]()
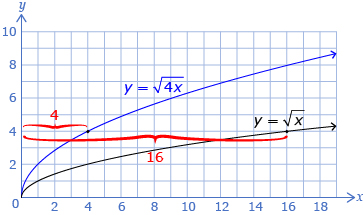
Even though the stretches are different, the resulting graphs are the same. Note: When analyzing radical functions, any stretch can be described as either a vertical stretch or a horizontal stretch.
Self-Check 3
- Consider the function
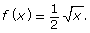
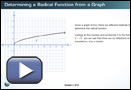
Up to this point, you have graphed radical functions using transformations. Now you will look at a graph and determine the radical function. View Determining a Radical Function from a Graph, which shows an example of how to write the radical function from a graph.
If you would like to see another example of determining a radical function from a graph, read through “Example 3” on pages 68 and 69 in the textbook.
Self-Check 4
1.10. Explore 6
Module 2: Radical Functions
Radical functions are used in different applications. Following is an example of how radical functions are used in physics.
Try This 5
After an accident, police determine the speed at which the car had been moving by applying a simple radical formula, ![]() The formula can be used to approximate the speed, v, in miles per hour, of a car that has left a skid mark of length, L, in feet.
The formula can be used to approximate the speed, v, in miles per hour, of a car that has left a skid mark of length, L, in feet.
- Describe the transformations required to produce the function
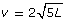 from the function
from the function 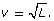
- Graph the function
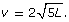
- State the domain and range. What do these values mean in the context of this question?
- Use the graph to determine how far a car will skid at 65 mph and at 100 mph.
If you would like to see another example of an application of a radical function, read through “Example 4” on pages 70 and 71 of the textbook.
Self-Check 5
Complete “Your Turn” on page 71 of the textbook. Answers
For a summary of graphing radical functions, you may choose to watch the video titled “Graphs of Square Root Functions.” If you feel comfortable graphing radical functions, you might prefer to skip the video.
Add the following formula to your copy of Formula Sheet:
1.11. Connect
Module 2: Radical Functions
Complete the Lesson 1 Assignment that you saved in your course folder at the beginning of the lesson. Show work to support your answers.
![]() Save your responses in your course folder.
Save your responses in your course folder.
Project Connection
You are ready to start working on the module project. Go to Module 2 Project: Pendulums, and read over all project requirements to become familiar with what you will be doing and how you will be assessed. Complete the first step of the project, Part 1: Transformation of a Radical Function.
1.12. Lesson 1 Summary
Module 2: Radical Functions
Lesson 1 Summary

iStockphoto/Thinkstock
In this lesson you saw how radical functions can be used in a variety of applications, including accident-scene investigations. You graphed radical functions and then answered questions using the graph and you determined the equation of a radical function from a given graph.
A radical function is a function where the variable is part of the radicand. The base radical function of ![]() has the shape of half of a parabola opening to the right. The domain is {x|x ≥ 0, x ∈ R} and the range is {y|y ≥ 0, y ∈ R}. You can graph radical functions by using transformations of the base function
has the shape of half of a parabola opening to the right. The domain is {x|x ≥ 0, x ∈ R} and the range is {y|y ≥ 0, y ∈ R}. You can graph radical functions by using transformations of the base function ![]() Using the form
Using the form ![]() you can describe the transformations of the base function
you can describe the transformations of the base function ![]()
| Parameter | Value > 0 | Value < 0 |
| a | Vertical stretch of graph of |
Vertical stretch of graph of |
| b | Horizontal stretch of graph of |
Horizontal stretch of graph of |
| h | Graph of |
Graph of |
| k | Graph of |
Graph of |
You can also determine the domain and range of any radical function using the ideas of transformations.
In Lesson 2 you will study how the graphs of a function and the square root of the same function are related.