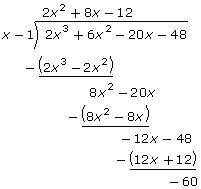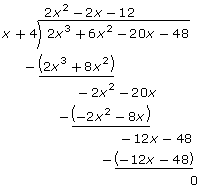Lesson 2
| Site: | MoodleHUB.ca 🍁 |
| Course: | Math 30-1 SS |
| Book: | Lesson 2 |
| Printed by: | Guest user |
| Date: | Tuesday, 9 December 2025, 11:17 PM |
Description
Created by IMSreader
1. Lesson 2
Module 3: Polynomial Functions
Lesson 2: Factoring Polynomials
Focus
You may look at the mountain range in the image and words like majestic, rugged, or wilderness might come to mind. How about the word polynomial?

Stockbyte/Thinkstock
Part of the contour of the peaks can be represented by a polynomial of degree 3.

adapted from Stockbyte/Thinkstock
In lesson 1 you saw how useful the expanded and factored forms of polynomial functions are for identifying end behavior and x- and y-intercepts. Up until now, you have been given the factored form for any polynomial of degree 3 or higher.
In this lesson you will learn how to determine the equivalent factored forms of cubic and higher-degree functions like the one modelling the mountain range.
Lesson Outcome
At the end of this lesson you will be able to factor polynomials of degree 3 and higher.
Lesson Questions
You will investigate the following questions:
- How is polynomial division related to numeric division?
- How do you know when a number or binomial is a factor of another number or polynomial?
Assessment
Your assessment may be based on a combination of the following tasks:
- completion of the Lesson 2 Assignment (Download the Lesson 2 Assignment and save it in your course folder now.)
- course folder submissions from Try This and Share activities
- additions to Glossary Terms and Formula Sheet
1.1. Discover
Module 3: Polynomial Functions
Discover
In elementary school you learned about the relationship between division and multiplication. For every division statement, there is a corresponding multiplication statement. Here are some examples:
| Division Statement | Corresponding Multiplication Statement |
| 6 ÷ 3 = 2 | 6 = 3 × 2 |
| 13 ÷ 5 = 2, remainder 3 | 13 = 5 × 2 + 3 |
| 16 ÷ 5 = 3, remainder 1 | 16 = 5 × 3 + 1 |

© WavebreakmediaMicro/37963742/Fotolia
The concepts and processes for factoring polynomials are very similar to the concepts and processes for factoring numbers. So, you will first reacquaint yourself with factoring numbers.
Although the ideas of factors may seem simple, there are some fundamental concepts that require exploration. Try This 1 and Share 1 will explore these concepts in more detail.
Try This 1
- What are the factors of 21?
- How do you know 5 is not a factor of 21?

![]() Save your responses in your course folder.
Save your responses in your course folder.
Share 1
With a partner or in a group, discuss the following question based on your responses to Try This 1:
What pattern do you see in the remainder when numbers are divided by factors versus non-factors?
![]() If required, save a record of this discussion in your course folder.
If required, save a record of this discussion in your course folder.
Writing division and multiplication statements may be helpful.
1.2. Explore
Module 3: Polynomial Functions
Explore
In Share 1 you may have concluded that factors of a number divide “evenly” into the number. For instance, 2 divides evenly into 16, but 5 does not. A more formal way to say this follows:
- When a number is divided by one of its factors, the remainder is zero.
- When a number is divided by a non-factor, the remainder is not zero.
The following examples illustrate this fact.
| Division Statement | Multiplication Statement | Conclusion |
| 15 ÷ 2 = 7, remainder 1 | 15 = 2 × 7 + 1 | Because the remainder is non-zero, 2 is not a factor of 15. |
| 15 ÷ 3 = 5, remainder 0 | 15 = 3 × 5 + 0 | Because the remainder is zero, 3 is a factor of 15. |
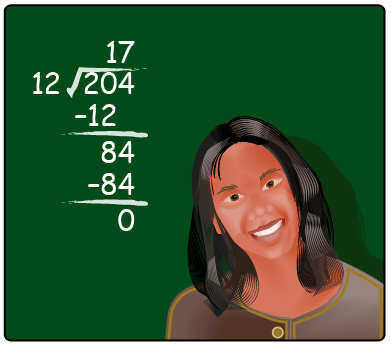
The idea that dividing a number by one of its factors results in a remainder of zero also applies to polynomials. So, how do you divide polynomials?
You may have learned “long division” of numbers in elementary school. The same process can also be used with polynomials.
Watch Polynomial Long Division to see how long division of polynomials is related to long division of numbers.

In the polynomial long division you just watched, both long-division questions resulted in non-zero remainders. This indicates that neither solution was a factor.
The result of dividing a polynomial can be written as a statement in the form ![]()
Read “Link the Ideas” and work through “Example 1” on page 120 of the textbook to learn more about this form and how it is used to express the division result. As you read, pay attention to how the restrictions on the variable are determined and how you can verify the solution.
1.4. Explore 3
Module 3: Polynomial Functions
So far in this lesson, you have used long division to divide polynomials by a binomial. If the binomial is a factor, the long division allows you to determine a second factor. The following example shows how this process can be used to fully factor a polynomial and then use the factored form to sketch the corresponding graph.
Example: Factor and then Sketch f(x) = 2x3 + 6x2 − 20x − 48
Try dividing f(x) by x − 1:
The remainder is not zero, so x − 1 is not a factor of 2x3 + 6x2 − 20x − 48. |
Try dividing f(x) by x + 4:
The remainder is zero, so x + 4 is a factor of 2x3 + 6x2 − 20x − 48. |
Now you can rewrite f(x) as f(x) = (x + 4)(2x2 − 2x − 12). But you can go further; 2x2 − 2x − 12 can also be factored:
2x2 − 2x − 12 = 2(x + 2)(x − 3)
The fully factored form of f(x) is f(x) = 2(x + 4)(x + 2)(x − 3).
You now have two equivalent forms of this function:
Expanded: f(x) = 2x3 + 6x2 − 20x − 48
Factored: f(x) = 2(x + 4)(x + 2)(x − 3)
f(x) is a cubic polynomial with a positive leading coefficient, so you know the graph starts in quadrant 3 and ends in quadrant 1. The y-intercept is −48. The equivalent factored form tells you there are x-intercepts at −4, −2, and 3.
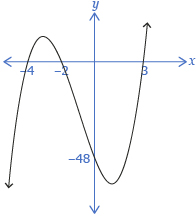

iStockphoto/Thinkstock
In the previous example the binomials x − 1 and x + 4 were tested to see whether or not they were factors of a cubic polynomial. It was a lot of work to do the long division just to discover that x − 1 was not a factor.
You need a better way to see whether or not a binomial is a factor—long division is far too much work for that task. Try This 2 will help you see patterns that can be used to reduce the effort for determining factors of a polynomial.
Try This 2
Complete questions 4 to 8 on page 119 of the textbook.
![]() Save your responses in your course folder.
Save your responses in your course folder.
1.5. Explore 4
Module 3: Polynomial Functions
You may have noticed a pattern in Try This 2 that mathematicians call the remainder theorem. The theorem simply states that when a polynomial is divided by the binomial x − a (where a is a particular number), the remainder will be the number obtained when a is substituted into the polynomial for x.
The formal way of stating this is when a polynomial in x, P(x), is divided by a binomial of the form x − a, the remainder will be P(a).1
Put together the following facts:
- Division resulting in a zero remainder tells you that you have a factor.
- The remainder when P(x) is divided by x − a is P(a).
Combining these facts results in what mathematicians call the factor theorem: x − a is a factor of a polynomial in x, P(x), if and only if P(a) = 0.2
In the following textbook example, you will see how the factor theorem can be used to identify factors by determining the remainder.
Read “Link the Ideas” on page 127 and “Example 1” on page 128 of the textbook. As you read, pay special attention to the sign of a substituted into the polynomials. For example, since the factor theorem states that the divisor must be in the form of x − a (note the minus sign), if −2 is the a-value, the corresponding divisor is x − (−2), which is normally written x + 2.
Remember that the factor theorem states that the divisor must be in the form x − a (note the minus sign). The way to write x + 4 in this form is to write x − (−4); therefore, the a-value is −4.
Going back to the example you read before Try This 2, f(x) = 2x3 + 6x2 − 20x − 48, it can quickly be determined that x − 1 is not a factor without doing tedious long division.
Similarly, it can quickly be determined that x + 4 is a factor; therefore, long division could be performed to find another factor of the polynomial.
Self-Check 2
![]()
- Complete questions 7 and 8 on page 124 of the textbook. Answer
- Complete questions 2.a., 2.c., 2.e. 3.a., 3.c., and 3.e. on page 133 of the textbook. Answer
1.6. Explore 5
Module 3: Polynomial Functions
When you are looking for a factor of a polynomial, how do you know what binomials to try?
In Try This 3 you will explore patterns that will help you determine which factors to try when you are trying to factor a polynomial.
Try This 3
-
- Use the factor theorem to determine if the following binomials are factors of the polynomial. Record your results in a table similar to the one that follows.
- Use the polynomials and factors listed in the table to determine the a-value of each factor. The first polynomial is already completed.
Polynomial Constant Term Factors x – a
a P(x) = x3 + 2x2 − 5x − 6 −6 x − 2 2 x + 1 −1 x + 3 −3 P(x) = x3 + x2 − 10x + 8 8 x − 1 x − 2 x + 4 P(x) = x4 + 2x3 − 13x2 − 14x + 24 24 x − 1 x − 3 x + 2 x + 4
- Compare the value of the constant term in each polynomial to the value of a, and describe any patterns you find.

- Try the pattern you discovered in question 2 and state the possible values of a for the polynomial P(x) = x3 − 6x2 + 5x + 12.
1.7. Explore 6
Module 3: Polynomial Functions
In Try This 3 you may have found that, when you are looking for a factor of a polynomial, you can try values that are factors of the constant term of the polynomial.
This is called the integral zero theorem. This theorem states that if x − a is a factor of a polynomial function P(x) with integral coefficients, then a is a factor of the constant term of P(x).1
Coming back to the example f(x) = 2x3 + 6x2 − 20x − 48, the factors of the constant term (−48) are ±1, ±2, ±3, ±4, ±6, ±8, ±12, ±16, ±24, and ±48; so these are the numbers to test as a-values.
Self-Check 3
Complete questions 4.a., 4.c., and 4.e. on page 133 of the textbook. Answer
1 Adapted from Pre-Calculus 12. Whitby, ON: McGraw-Hill Ryerson, 2011. Reproduced with permission.
1.8. Explore 7
Module 3: Polynomial Functions
A lot of new information has been introduced in this lesson. Here is a summary of how the information fits together.
| Example | Mathematical Justification |
| In order to sketch f(x) = 2x3 + x2 – 13x + 6, you need to create an equivalent factored form. | The factors correspond to x-intercepts. |
Test for factors:
f(1) = −4
f(−1) = 18
f(2) = 0 x − 2 is a factor of f(x) because f(2) = 0. |
The remainder theorem tells you that f(a) = the remainder when f(x) is divided by x − a.
The factor theorem tells you to look for values of a such that f(a) = 0. The integral zero theorem tells you to try factors of the constant term of f(x). (In this example, 6.) |
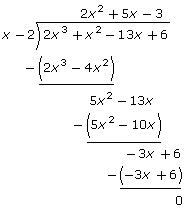 |
Perform division to determine a second factor. |
| f(x) = (x − 2)(2x2 + 5x − 3) | This equivalent factored form can be written using f(x) = (x − a)Q(x) + R, where Q(x) is the quotient and R is the remainder. |
| f(x) = (x − 2)(x + 3)(2x − 1) | The equivalent factored form of 2x2 + 5x − 3 is (x + 3)(2x − 1). |
The graph of f(x) will have x-intercepts at 2, −3, and
|
These are the values that make each factor equal to zero, thus making f(x) = 0. |
1.9. Explore 8
Module 3: Polynomial Functions
![]()
Self-Check 4
Complete questions 5.a., 5.c., 5.d., and 10 on page 134 of the textbook.
Add the following terms to your copy of Glossary Terms:
- factor theorem
- integral zero theorem
- polynomial division
- remainder theorem
Add the following formula to your copy of Formula Sheet:
![]()
1.10. Connect
Module 3: Polynomial Functions
Complete the Lesson 2 Assignment that you saved in your course folder at the beginning of the lesson. Show work to support your answers.
![]() Save your responses in your course folder.
Save your responses in your course folder.
Project Connection
There is no Project Connection in this lesson.
1.11. Lesson 2 Summary
Module 3: Polynomial Functions
Lesson 2 Summary
In this lesson you learned how to factor polynomials of degree 3 or higher. You learned
- polynomial long division
- the remainder theorem: when a polynomial in x, P(x), is divided by a binomial of the form x − a, the remainder will be P(a)
- the factor theorem: x − a is a factor of a polynomial in x, P(x), if and only if P(a) = 0
- the integral zero theorem: if x − a is a factor of a polynomial function P(x) with integral coefficients, then a is a factor of the constant term of P(x)
In the next lesson you will learn to solve polynomial equations. You will relate solutions to equations to the factors of polynomials and x-intercepts of their graphs.
Adapted from Pre-Calculus 12. Whitby, ON: McGraw-Hill Ryerson, 2011. Reproduced with permission.