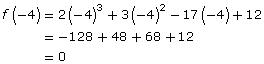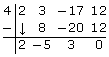Lesson 3
| Site: | MoodleHUB.ca 🍁 |
| Course: | Math 30-1 SS |
| Book: | Lesson 3 |
| Printed by: | Guest user |
| Date: | Tuesday, 9 December 2025, 11:17 PM |
Description
Created by IMSreader
1. Lesson 3
Module 3: Polynomial Functions
Lesson 3: Solving Polynomial Equations
Focus

iStockphoto/Thinkstock
Designers may describe curves using polynomials, but polynomials can be used to help plan materials for a project. To produce a final product, a designer could use polynomials to describe the materials required to cover a specific area. Could a polynomial function be used to describe the amount of material required to produce a quilt?
In this lesson you will solve polynomial equations of degree 3 and higher. As part of the process, you will learn mathematically equivalent, but faster, methods for determining possible factors of polynomials and performing polynomial division.
Lesson Outcomes
At the end of this lesson you will be able to
- use the zero-product property when solving polynomial equations
- use a faster method for determining possible factors of polynomials
- divide polynomials using synthetic division
Lesson Questions
You will investigate the following questions:
- How do you solve polynomial equations involving polynomials of degree 3 or higher?
- How are solutions to equations, factors of polynomials, and x-intercepts of graphs related to one another?
Assessment
Your assessment may be based on a combination of the following tasks:
- completion of the Lesson 3 Assignment (Download the Lesson 3 Assignment and save it in your course folder now.)
- course folder submissions from Try This and Share activities
- additions to Glossary Terms
- work under Project Connection
1.1. Launch
Module 3: Polynomial Functions
Launch
Do you have the background knowledge and skills you need to complete this lesson successfully? Launch will help you find out.
This lesson relies heavily on the following skills from Lesson 2:
- division of polynomials by binomials
- using the integral zero and factor theorems to determine binomial factors of polynomials
1.2. Discover
Module 3: Polynomial Functions
Discover

iStockphoto/Thinkstock
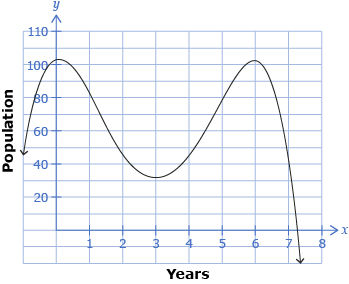
Isabel is a researcher studying whooping crane populations in a particular area. She has determined that, due to natural fluctuations between predators and the whooping cranes, the population can be modelled by the following function, where p is the population after x years:
p(x) = −x4 + 12x3 − 37x2 + 6x + 101
She has determined that this function will be valid for the next 7 yr.
In 1945, there were just 15 whooping cranes in North America, and the species was declared endangered in 1971.
Isabel would like to determine when the population will be 45 whooping cranes. One way to solve this problem is graphically, by drawing a horizontal line at 45 and determining where the line crosses the population curve.
Based on this graph, it appears that the population will be 45 after 2, 4, and 7 yr.
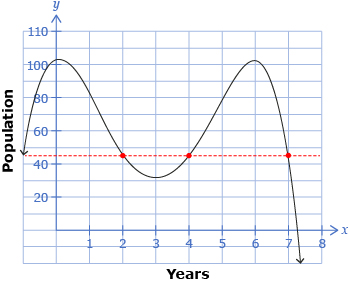
However, Isabel remembered how much fun she had learning about polynomials in Mathematics 30-1, so she decided to solve the problem algebraically. This corresponds to solving the equation p(x) = 45.
−x4 + 12x3 − 37x2 + 6x + 101 = 45
As a first step in learning how to solve this equation, complete Try This 1.
Try This 1
Solve the following quadratic equations. Make note of any similarities and differences in how you solved the equations.
- w2 − 3w − 10 = 0
- w2 + w − 9 = 3
Share 1
With a partner or in a group, share your solutions from Try This 1. How was your first step in solving the first equation different from the first step in solving the second equation?
![]() If required, save a record of your discussion in your course folder.
If required, save a record of your discussion in your course folder.
1.3. Explore
Module 3: Polynomial Functions
Explore
In Try This 1 you may have concluded that in order to solve polynomial equations, one side of the equal sign must be zero. When one side of the equal sign is zero, the zero-product property can be used. (If the product of 2 or more numbers is zero, then one or more of the numbers must be zero.)
Based on this information, Isabel decided to subtract 45 from both sides of her equation to get an equivalent equation.
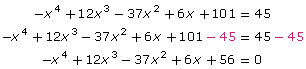
In order to use the zero-product property, −x4 + 12x3 − 37x2 + 6x + 56 needs to be factored.
How to Factor Polynomials
Step 1: For any polynomial, f(x)
- the remainder theorem tells you that f(a) = the remainder when f(x) is divided by x − a
- the factor theorem tells you to look for values of a such that f(a) = 0
- the integral zero theorem tells you to try factors of the constant term of f(x) for values of a
Step 2: Use the factor theorem to determine one factor of f(x).
Step 3: Perform polynomial division to determine a second factor.
Step 4: This equivalent factored form can be written as f(x) = (x− a)Q(x) + R, where Q(x) is the quotient and R is the remainder.
Step 5: Repeat until all factors have been identified.
In Lesson 1 you learned that the x-intercepts of a polynomial’s graph correspond to the polynomial’s factors. You used the factors to determine the x-intercepts. You can also use this process in reverse: use the x-intercepts to determine potential factors.
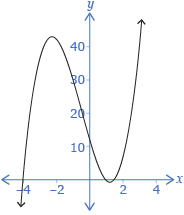
Here is the graph of the function f(x) = −x4 + 12x3 − 37x2 + 6x + 56.
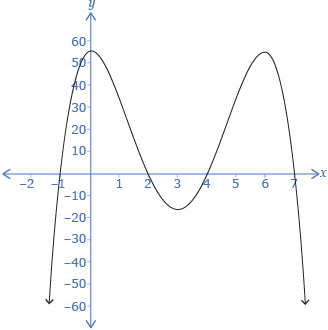
Share 2
With a partner or in a group, discuss why f(x) = −x4 + 12x3 − 37x2 + 6x + 56 was graphed instead of p(x) = −x4 + 12x3 − 37x2 + 6x + 101.
![]() If required, save a record of your discussion in your course folder.
If required, save a record of your discussion in your course folder.
1.4. Explore 2
Module 3: Polynomial Functions
Looking at the graph, it appears that x = 7 is an x-intercept. If that is true, that would mean x − 7 is a factor. So, test x − 7 using the factor theorem.
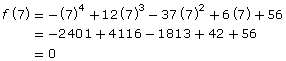

© Elenathewise/7542025/Fotolia
Just because it looks like x = 7 is an x-intercept, doesn’t mean that it is. Maybe the x-intercept is very close to 7 (like 7.001)—you would not be able to tell this from the graph. As a result, you must test what might be a factor using the factor theorem.
In this case you have determined that x − 7 is a factor. Isabel needs to perform the following division to determine another factor:
That is going to be a lot of work. Fortunately, there is a faster, mathematically equivalent process, called synthetic division. Watch Synthetic Division to see how the process works.
Self-Check 1
Complete questions 4.a., 4.b., and 4.c. on page 124 of the textbook.
Try This 2
Back to Isabel and the whooping cranes. Previously it was determined that x − 7 is a factor of −x4 + 12x3 − 37x2 + 6x + 56. Use long division or synthetic division, whichever you prefer, to determine another factor. Continue factoring until you have written −x4 + 12x3 − 37x2 + 6x + 56 as the product of four binomial factors.
![]() Save your responses in your course folder.
Save your responses in your course folder.
1.5. Explore 3
Module 3: Polynomial Functions
The equivalent factored expression you should have created in Try This 2 is −1(x − 7)(x + 1)(x − 4)(x − 2).
Substituting this into the equation at the beginning of the Explore section results in the following equation that can be used to determine when the whooping crane population is 45:
−1(x − 7)(x + 1)(x − 4)(x − 2) = 0
Try This 3
Use your knowledge of the zero-product property to solve the equation −1(x − 7)(x + 1)(x − 4)(x − 2) = 0. ![]()
- Using the idea of the zero-product property, what should each factor of the polynomial equation −1(x − 7)(x + 1)(x − 4)(x − 2) = 0 equal?
- Solve for x in the equation −1(x − 7)(x + 1)(x − 4)(x − 2) = 0.
- Which solutions for x are reasonable answers to the question involving the population of whooping cranes over time?
![]() Save your responses in your course folder.
Save your responses in your course folder.
1.6. Explore 4
Module 3: Polynomial Functions
You should have concluded that x = 7, 4, 2, and −1 are solutions to the equation. The whooping crane population will be 45 after 2, 4, and 7 years. Since Isabel is looking forward and not backward, −1 is not used.
Many steps were used to solve this problem. Here is a summary of how to solve polynomial equations.
| Example | Mathematical Justification |
| Solve 2x3 + 3x2 − 17x + 7 = −5. | Your teacher asked you to solve this. |
| 2x3 + 3x2 − 17x + 12 = 0 | Add 5 to both sides to create an equivalent equation where the zero-product property can be used. |
| The factors of 12 are ±1, ±2, ±3, ±4, ±6, ±12. | The integral zero theorem says to check factors of the constant term using the factor theorem. |
Graph f(x) = 2x3 + 3x2 − 17x + 12:
|
Rather than testing all of the factors of 12, graph the function and look for x-intercepts, because x-intercepts correspond to factors. |
Test for a factor of x + 4.
|
It appears that x = −4 is an x-intercept. This would correspond to a factor of x − (−4), which is normally written as x + 4. The factor theorem says that x − a is a factor of P(x) if P(a) = 0. |
Perform (2x3 + 3x2 − 17x + 12) ÷ (x + 4).
2x3 + 3x2 − 17x + 12 = (x + 4)(2x2 − 5x + 3) |
x + 4 is a factor, so divide by this factor to determine another factor.
This example uses synthetic division, but you can use long division (from Lesson 2) if you prefer. |
2x2 − 5x + 3 = (2x − 3)(x − 1) 2x3 + 3x2 − 17x + 12 = (x + 4)(2x − 3)(x − 1) |
The quadratic can also be factored. |
| (x + 4)(2x − 3)(x − 1) = 0 | Rewrite the equation using this equivalent factored form so the zero-product property can be used. |
x + 4 = 0
2x − 3 = 0 x − 1 = 0 |
Apply the zero-product property. |
| Solve. These are the solutions to the original equation.
|
1.7. Explore 5
Module 3: Polynomial Functions
Self-Check 2
![]()
- Complete questions 1.a. and 2.a. on page 147 of the textbook. Answer
- Solve the polynomial equation 2x3 − 5x2 − x + 10 = 4 algebraically. Answer
You will need to remember the following definitions in order to complete Try This 4.
zeros of a polynomial: values of the variable that make the polynomial equal to zero; for example, the zeros of the polynomial p(x) = (x − 1)(x + 2) are x = 1 and x = −2
roots of an equation: values of the variable that make the left side of the equation equal to the right side of the equation
In this module you worked with polynomials in expanded and factored form, polynomial equations, and graphs of polynomial functions. In Try This 4 and Share 3 you will investigate relationships among zeros, roots, and x-intercepts.
Try This 4
Refer to question 2 of Self-Check 2 to answer the following questions.
- How is the original equation 2x3 − 5x2 − x + 10 = 4 from question 2 of Self-Check 2 related to the equation 2x3 − 5x2 − x + 6 = 0?
- Using technology, graph f(x) = 2x3 − 5x2 − x + 6. How are the x-intercepts of the graph of f(x) = 2x3 − 5x2 − x + 6 related to the roots of the equation?
- How are the roots of the equation related to the zeros of the polynomial p(x) = 2x3 − 5x2 − x + 6?
![]() Save your responses in your course folder.
Save your responses in your course folder.
Share 3
With a partner or in a group, summarize the relationship between the zeros of the polynomial, the roots of the equation, and the x-intercepts of the graph of the polynomial.
![]() If required, save a summary of your discussion in your course folder.
If required, save a summary of your discussion in your course folder.
1.8. Explore 6
Module 3: Polynomial Functions
In Try This 4 and Share 3 you may have discovered that the following values are identical when given a polynomial equation with one side equal to zero:
- the zeros of the polynomial
- the roots of the equation
- the x-intercepts of the graph of the polynomial
These relationships are illustrated in Zeros, Roots, x-intercepts.
Having zero on one side of the equation is crucial. If the equation had been something like (2x − 3)(x + 1)(x − 2) = 7 (note the 7 instead of 0), the zeros of the polynomial on the left side ![]() would not be the same as the root of the equation (x = 2.7481…)
would not be the same as the root of the equation (x = 2.7481…)
Self-Check 3
![]()
- Complete questions 3.a., 3.b., and 5 on page 148 of the textbook. Answers
- Complete question 12 on page 150 of the textbook. Answer
- At the beginning of the lesson, the idea of using polynomials to determine the amount of material required for a project was discussed. You will now use a polynomial to determine the dimenstions of a wall hanging. Complete question 18 on page 151 of the textbook. Answers
Add the following terms to your copy of Glossary Terms:
- synthetic division
- zeros of a polynomial
- roots of an equation
1.9. Connect
Module 3: Polynomial Functions
Complete the Lesson 3 Assignment that you saved in your course folder at the beginning of the lesson. Show work to support your answers.
![]() Save your responses in your course folder.
Save your responses in your course folder.
Project Connection
Go to Module 3 Project: Graphic Design Using Polynomials and complete Part 2 and Conclusion.
![]() Save your responses in your course folder.
Save your responses in your course folder.
1.10. Lesson 3 Summary
Module 3: Polynomial Functions
Lesson 3 Summary
In this lesson you learned how to solve polynomial equations. In particular, you learned
- one side of the equation must be zero so the zero-product property can be used
- synthetic division of polynomials
- that there is a one-to-one correspondence among zeros of polynomials, x-intercepts of graphs, and roots of equations