Print bookPrint book

Lesson 3

Site: MoodleHUB.ca 🍁
Course: Math 30-1 SS
Book: Lesson 3
Printed by: Guest user
Date: Tuesday, 9 September 2025, 7:09 AM

Description

Created by IMSreader

Table of contents

1. Lesson 3

Mathematics 30-1 Module 4

Module 4: Foundations of Trigonometry

 

Lesson 3: The Unit Circle

 
Focus

 

This is a photo of water ripples formed as circles coming from a central point.

Photos.com/Thinkstock

How many circles can you count in the water ripple shown in the photograph? The circles are different sizes. How can you describe their sizes?

 

So far in this module you have learned about radian angle measure and arc length. You used proportions to determine the radian measure of an angle when given the angle in degrees. You also learned how to determine the length of an arc on a circle.



Many trigonometric problems can be simplified by referencing a circle with a particular radius. What radius do you think would make both radians and arc lengths easiest to work with?

 

 
This sketch shows an angle in standard position with the terminal arm in the third quadrant. An unknown radius is labelled on the initial arm.

 

Lesson Outcomes

 

At the end of this lesson you will be able to

  • derive the equation of the unit circle
  • determine the coordinates of points of intersection of an angle’s terminal arm and the unit circle
  • generalize the equation of a circle with centre (0, 0) and radius r
Lesson Questions

 

You will investigate the following questions:

  • How is an equation of a unit circle derived?
  • How are points on the unit circle determined?
Assessment

 

Your assessment may be based on a combination of the following tasks:

  • completion of the Lesson 3 Assignment (Download the Lesson 3 Assignment and save it in your course folder now.)
  • course folder submissions from Try This and Share activities
  • additions to Glossary Terms and Formula Sheet
Materials and Equipment

 

You will need

  • paper
  • scissors
  • tape
  • can or other cylinder
  • straight edge


1.1. Launch

Mathematics 30-1 Module 4

Module 4: Foundations of Trigonometry

 

Launch

 

Do you have the background knowledge and skills you need to complete this lesson successfully? Launch will help you find out.

 

Before beginning this lesson you should be able to

  • determine the sine, cosine, and tangent ratios for right triangles
  • determine the exact values of the sides of reference triangles 30°-60°-90° and 45°-45°-90°
  • rationalize denominators of rational numbers


1.2. Are You Ready?

Mathematics 30-1 Module 4

Module 4: Foundations of Trigonometry

 

Are You Ready?
 

Complete these questions. If you experience difficulty and need help, visit Refresher or contact your teacher.

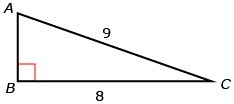
  1. Look at the triangle shown.

     
    This diagram shows a right triangle with hypotenuse of length 9 and one other side of length 8.

    1. Determine the unknown side of the triangle. Answer

    2. Determine the sine, cosine, and tangent ratios for the triangle. Leave your answers in the form of a ratio. Answer
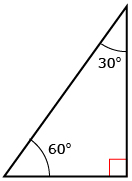
  2. A 30°-60°-90° triangle is shown.

     
    This diagram shows a right triangle. The other two angles are 60 degrees and 30 degrees.
    1. If the hypotenuse has a length of 2 and the length of the horizontal leg is 1, determine the exact value of the length of the vertical leg. Answer
    2. Determine the exact value of sin 30°. Answer
    3. Determine the exact value of sin 150°. Answer
  3.  
    1. Draw a triangle with angles 45°, 45°, and 90°. Answer
    2. If the hypotenuse has a length of determine the exact value of the length of the other two sides. Answer
    3. Determine the exact value of sin 45° and cos 45°. Answer
  4. Rationalize the denominators in the following fractions.
    1.  Answer
    2.  Answer

If you answered the Are You Ready? questions without difficulty, move to Discover.

 

If you found the Are You Ready? questions difficult, complete Refresher.



1.3. Refresher

Mathematics 30-1 Module 4

Module 4: Foundations of Trigonometry

 

Refresher

 

This is a play button that opens Mathematics 20-1 Learn EveryWare Module 2: Lesson 1 Summary.

Read the Mathematics 20-1 Learn EveryWare Module 2: Lesson 1 Summary to review sine, cosine, and tangent ratios.


This is a play button that opens Mathematics 20-1 Learn EveryWare Module 2: Lesson 3 Summary.

Read the Mathematics 20-1 Learn EveryWare Module 2: Lesson 3 Summary to review 30°-60°-90° and 45°-45°-90° triangles.


This is a play button that opens Using a 30-60-90 Triangle for a 150 Angle.

Watch Using a 30-60-90 Triangle for a 150° Angle to review using a 30°-60°-90° triangle to determine the exact values of sine and cosine ratio.


This is a play button that opens Pythagorean Theorem.

Read the definition and work with the applet in Pythagorean Theorem.


This is a play button that opens Rationalizing the Denominator.

Watch Rationalizing the Denominator.



Go back to the Are You Ready? section and try the questions again. If you are still having difficulty, contact your teacher.



1.4. Discover

Mathematics 30-1 Module 4

Module 4: Foundations of Trigonometry

 

Discover
 
Try This 1

 

This is a photo of two cylindrical cans. One is upright and the other is on its side.

iStockphoto/Thinkstock

You want to unwrap some information about the circumference of a tin can. You don’t want to cut the can, so you need to think of another way to unwrap the information. How does the circumference of a tin can relate to radian measures in a circle?


 

textbook

  1. Complete “Investigate Circular Number Lines” parts 1 to 7 on pages 180 and 181 of the textbook. Watch Investigate Circular Number Lines to see the steps explained.

     
    This is a play button that opens Investigate Circular Number Lines.
  2. Since each number line shows the circumference of the can and the circle to be 2π units, what assumption is being made about the length of the radius?1
  3.  
    1. Determine the coordinates for 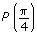. Start by marking the coordinates for all the points on the circle that are midway between the axes.

       
      This diagram shows a circle divided into 8ths with the centre marked O. The horizontal division on the right side is labelled P at zero equals 1, 0. The first division counterclockwise from this point is labelled pi divided by 4.
      Adapted from Pre-Calculus 12. Whitby, ON: McGraw-Hill Ryerson, 2011. Reproduced with permission.
    2. What is the only difference in the coordinates for these four points that are midway between the axes?

course folder Save your responses in your course folder.

 

Share 1

 

With a partner or in a group, compare your responses from Try This 1 questions 2 and 3 and the methods you used to determine the coordinates for the eight points.

 

course folder If required, save a record of your discussion in your course folder.

 

1 Source: Pre-Calculus 12. Whitby, ON: McGraw-Hill Ryerson, 2011. Reproduced with permission.

Draw a vertical line from point P to the horizontal axis. Use properties of the 45°-45°-90° triangle that you already know to determine the lengths of the sides of the triangle.


1.5. Explore

Mathematics 30-1 Module 4

Module 4: Foundations of Trigonometry

 

Explore

 

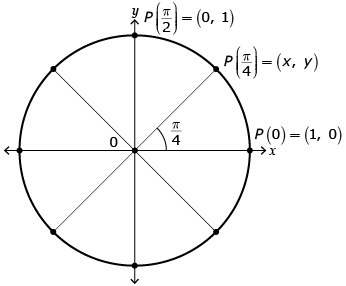
In Try This 1 you took a circle and divided it into sections that were multiples of  and You may have determined that the radius of the circle you made is 1 unit, since the distance around the circle, or the circumference, was 2π.

 

 


 

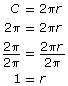
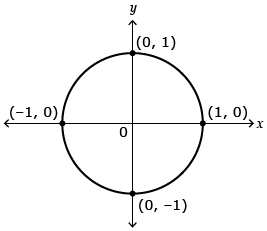
This is a sketch of a unit circle. The centre is at the origin and the points 1, 0; 0, 1; negative 1, 0; and 0, negative 1 are labelled on the circle.

Source: Adapted from Pre-Calculus 12. Whitby, ON: McGraw-Hill

Ryerson, 2011. Reproduced with permission.

A circle with a radius of 1 and the centre at the origin can be called a unit circle.

 

Now that you have found some values for points on a unit circle, you can derive an equation to represent all points on a unit circle. You will use the Pythagorean theorem.

 

Try This 2

 

Step 1: Draw a unit circle on an x- and y-axis. This means that you will draw a circle with a radius of 1 and the centre of the circle at the origin (0, 0).

 

Step 2: Label the centre of the circle O.

 

Step 3: Pick any point in quadrant 1 of the unit circle. Label the point P(x, y).

 

Step 4: Draw a line from point O to point P. What is the length of this line segment?

 

Step 5: Label OP on the diagram.

Step 6: Create a right-angle triangle by drawing a vertical line from point P to the x-axis. Label the point on the x-axis A.

  1. What is the length of line segment PA? Label this length.
  2. What is the length of line segment OA? Label this length.
  3. Since this is a right-angle triangle, use the Pythagorean theorem to write an equation that relates the lengths of OP, PA, and OA.

course folder Save your responses in your course folder.

 

Share 2

 

With a partner or in a group, discuss the following questions.

  1. Share the equation you wrote in Try This 2 question 3.
  2. Would your equation change if you chose a different point P?
  3. What would happen if point P were in quadrant 3? Would this change the lengths of PA and OA?

 course folder If required, save a record of your discussion in your course folder.

This will not be a number. Instead, a variable from the coordinate P(x, y) will describe this length.
This will not be a number. Instead, a variable from the coordinate P(x, y) will describe this length.

Your diagram should look something like this:

 

 

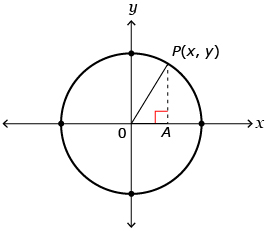
This is a diagram of a circle with its centre at the origin and point P(x, y) labelled in quadrant 1. A vertical line is drawn from P to the x-axis. The line is perpendicular to the x-axis.

Source: Pre-Calculus 12. Whitby, ON: McGraw-Hill
Ryerson, 2011. Reproduced with permission.

This is the radius of the circle.


1.6. Explore 2

Mathematics 30-1 Module 4

Module 4: Foundations of Trigonometry

 

In Try This 2 you derived the equation for the unit circle, x2 + y2 = 1. Any point that is on the unit circle will satisfy this equation.



textbook

Compare what you did in Try This 2 with the derivation of the equation for the unit circle on page 182 of the textbook. Note any differences and similarities you see.

The equation x2 + y2 = 1 only describes a circle that has a radius of 1; but you have seen that circles can have different radii, such as the circles in an archery target or the water ripples you saw in Focus. How can you write equations for circles with different radii?

 

 

This is a picture of an archery target.

 

Stockbyte/Thinkstock



textbook

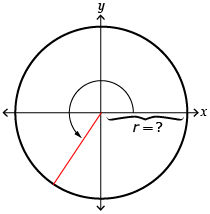
Read “Example 1” on page 182 of the textbook. Notice how the Pythagorean theorem is used to write the equation for a circle with a radius of 2.


Watch Equation of a Unit Circle to see how the Pythagorean theorem can be used to write the equation of a circle with centre (0, 0) at the origin and any radius length represented by r.

 

 
This is a play button that opens Equation of a Unit Circle.

 

Self-Check 1


textbook

Complete question 1.b. on page 186 of the textbook. Answer



1.7. Explore 3

Mathematics 30-1 Module 4

Module 4: Foundations of Trigonometry

 

When you are working with the unit circle, you know the equation for the circle is always x2 + y2 = 1. This is because the radius of the circle is 1. Could you determine if a point were on the unit circle if you knew both coordinates? Could you determine the x-coordinate if you knew the y-coordinate and that the point was on the unit circle?

 

Try This 3
  1. Is the point 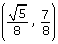on the unit circle?
  2. You will determine the y-coordinate for all points on the unit circle if the x-coordinate of the point is .
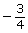    1. Draw a diagram indicating where this point could be located on the unit circle.
    2. Use the equation of the unit circle to help determine the y-coordinate.

course folder Save your responses in your course folder.

Substitute the x-coordinate into the equation x2 + y2 = 1, and then solve for y. Remember that when you take the square root of a number, the answer could be positive or negative.

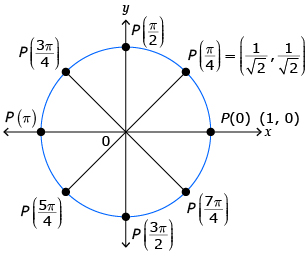
There is more than one point on the unit circle where the x-coordinate is . It's important that you get this answer correct. Check to see if your image matches the image shown here.

 

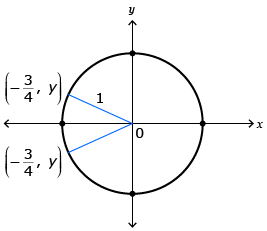
This is a picture of a circle on an x- and y-axis with the center at (0, 0) and radius of 1. There are two terminal arms, one in quadrant two and one in quadrant three. The two points that the terminal arms and circle intersect at are labelled negative 3 quarters and y.
Source: Pre-Calculus 12. Whitby, ON: McGraw-Hill Ryerson, 2011.
Reproduced with permission.

 



Coordinates that are on the unit circle must satisfy the equation of the unit circle, x2 + y2 = 1.

1.8. Explore 4

Mathematics 30-1 Module 4

Module 4: Foundations of Trigonometry

 

In Try This 3 you looked at how the equation of the unit circle, x2 + y2 = 1, could be used to determine if points were on the unit circle. You may have substituted both the x- and y-coordinates into the equation for the unit circle and determined if the two sides of the equation were equal.

 

In Try This 3 question 2 you were asked to determine the y-coordinate when given the x-coordinate. Your answer should have looked something like the solution shown here. There are two solutions because the x-coordinate can be negative in both quadrants 2 and 3.

 

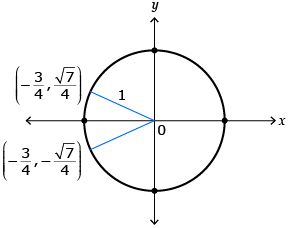
This is a sketch of a circle on an x- and y- axis with the centre at (0, 0) and a radius of 1. There are two terminal arms: one in quadrant two and one in quadrant three. The two points that the terminal arms and circle intersect at are labelled negative 3 quarters and the square root of 7 divided by 4; and negative 3 quarters and negative square root of 7 divided by 4.



textbook

Read “Example 2” on page 183 of the textbook. Note the following as you read:

  • The equation of the unit circle is used to determine the other coordinate.
  • Remember that when you take the square root of a number, the answer could be positive or negative.
  • Unless the quadrant is given in the question, it is important to determine the quadrants the coordinate could be in.
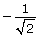  •   becomes  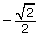at the end of the example. This is sometimes done so there are no radicals in the denominator. See the information on rationalizing denominators in Refresher if you need to review how this change is completed.

textbook
Self-Check 2

 

Complete questions 2.a., 2.f., 3.b., and 3.f. on pages 186 to 187 in the textbook. Answer

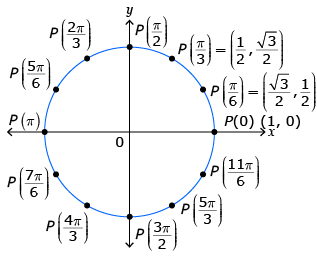
In Try This 1 you created two number lines that formed two circles. One circle divided into 8 equal parts, and one circle divided into 12 equal parts. In Share 1 you were asked to determine the coordinates for . You will use your answer to Try This 1 in Try This 4.

 

Try This 4

 

You will use Unit Circle Template to help organize the intersection points of terminal arms of angles and the unit circle. Print Unit Circle Template now.

  1. Fill in the central angle measurements for each terminal arm in the template using the circles you created in Try This 1. Remember that these circles were created by using a number line from 0 to 2π and then dividing the number line into 8 or 12 equal parts. Place each angle in the terminal-arm spaces on the template. The first quadrant has been completed for you.
  2. Fill in the x- and y-coordinates of the point of intersection of the terminal arm for the central angle 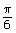 and the unit circle. Watch Finding Coordinates Example for help in determining the coordinate ( ___, ___ ) on your template.

     
    This play button opens Finding Coordinates Example.

 

textbook

  1. Use your knowledge of angles in all four quadrants to fill in all of the spaces in Unit Circle Template. Think about when x- and y-coordinates should be positive or negative.

    While answering question 3, read “Example 3” on pages 184 and 185 in the textbook. Notice that the angle 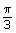can be placed in all four quadrants and then the coordinates determined.

course folder Save your responses in your course folder.

 

You will use your unit circle in future lessons of this module.

 

Share 3

 

With a partner or in a group, discuss the following questions.

  1. Examine the angles on your unit circle. Describe any patterns you see.

 

textbook

  1. Examine the coordinates on your unit circle. Complete question 11 on page 188 in your textbook.

course folder If required, save a record of your discussion in your course folder.



These are the two triangles that you can work with to help determine the coordinates. The given reference triangles have angles written as radians instead of degrees and have hypotenuses of  and 2, but the unit circle has a radius of 1. Using similar triangles you can create reference triangles with a hypotenuse of 1 to match the radius of the unit circle.

 

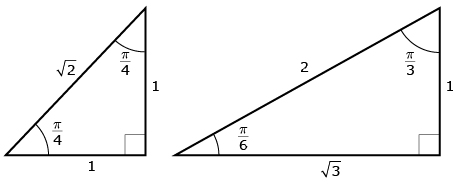
The diagram shows two triangles. The first triangle has angles pi divided by 4, pi divided by 4, and a right angle. The side length opposite both angles measuring pi divided by 4 is 1. The length of the hypotenuse opposite the right angle is the square root of 2.

1.9. Explore 5

Mathematics 30-1 Module 4

Module 4: Foundations of Trigonometry

 

In Try This 4 you created your own unit circle. Compare your unit circle to the one provided in The Unit Circle. Click on the 4, 8, and 12 buttons to see all of the values you completed in Try This 4.

 

 
This is a play button that opens The Unit Circle.

 

The applet can be used to determine the coordinates of a point on the circle given an angle of rotation. The applet can also be used to determine the angles of rotation in standard position when given the coordinates of the point on the unit circle.

 

Self-Check 3

 

Use your unit circle from Try This 4 to answer the following questions.

  1. If P(θ) is the point at the intersection of the terminal arm of angle θ and the unit circle, determine the coordinates of  on the unit circle as exact values. Answer
  2. Determine the central angle θ in the interval of  such that Answer

 

textbook

  1. Complete questions 4.b., 4.c., 4.g., 5.a., 5.e., and 6 on page 187 of the textbook. Answer
tip

You will want to keep the unit circle you created to use in upcoming lessons.

 

A copy of the unit circle will not be provided with the Diploma Exam. If you want to use the unit circle on the exam, you will need to remember a way to determine the angles and corresponding coordinates for the points on the unit circle. There are different strategies to do this. It is best to develop your own way to remember the patterns. You can search the Internet using the keywords “remembering the unit circle” for some ideas.



glossary

Add unit circle to your copy of Glossary Terms.

 

 




formula

Add the formula for the unit circle, x2 + y2 = 1, to your copy of Formula Sheet.



1.10. Connect

Mathematics 30-1 Module 4

Module 4: Foundations of Trigonometry

 

Connect

 

Lesson 3 Assignment


assessment

Complete the Lesson 3 Assignment that you saved in your course folder at the beginning of the lesson. Show work to support your answers.

 

course folder Save your responses in your course folder.

 

Project Connection

 

There is no Project Connection in this lesson.

 

Going Beyond

 

In this lesson you learned a lot about the unit circle. Your new understanding will be valuable as you continue your study of trigonometry. Another way to look at the unit circle is to unwrap the circle to form the graphs of the sine, cosine, and tangent functions. Try this out for yourself in ExploreLearning’s “Unit Circle.”

 

 

This is a play button that opens �Unit Circle.�

Screenshot reprinted with
permission of ExploreLearning

 



1.11. Lesson 3 Summary

Mathematics 30-1 Module 4

Module 4: Foundations of Trigonometry

 

Lesson 3 Summary

 

This is a picture of a colour wheel made of puzzle pieces.

© 3d_kot/35917383/Fotolia

The equation of the unit circle is x2 + y2 = 1 with its centre at (0, 0) and radius of 1. This equation can be derived from the Pythagorean theorem. This equation can be used to determine if a point is on the unit circle or to determine the value of the x- or y-coordinate when given one of the values.

 

You looked at specific points on the unit circle that correspond to eight or twelve equal parts of the circle. You wrote the coordinates of the specific points as exact values. Patterns can be used to help determine these points on the unit circle. The unit circle can be used to determine specific rotational angles when given the coordinates of a point and vice versa.

 

This is a unit circle divided into eight equal parts with each point labelled.

Source: Pre-Calculus 12. Whitby, ON: McGraw-Hill Ryerson, 2011. Reproduced with permission.

This is a unit circle divided into twelve equal parts with each point labelled.

Source: Pre-Calculus 12. Whitby, ON: McGraw-Hill Ryerson, 2011. Reproduced with permission.


In the next lessons you will see how the unit circle can be used to determine both angles and trigonometric ratios.