Lesson 3
| Site: | MoodleHUB.ca 🍁 |
| Course: | Math 30-1 SS |
| Book: | Lesson 3 |
| Printed by: | Guest user |
| Date: | Tuesday, 9 December 2025, 11:13 PM |
Description
Created by IMSreader
1. Lesson 3
Module 5: Trigonometry Applications and Identities
Lesson 3: Trigonometric Identities
Focus

red car: iStockphoto/Thinkstock; green car: iStockphoto/Thinkstock
Success in Formula 1 racing requires a powerful, lightweight, high-performance engine that is durable. For maximum speed and fuel efficiency, an aerodynamic design is used. The cockpit, also called the survival cell, is created out of carbon fibre and is designed with multiple safety features.
Suppose you own two race cars that are identical except for the colour. Would you expect the two cars to perform the same? Does it matter which car you race with? Is it reasonable to switch one car for the other and expect a similar result?
In this lesson you will learn about mathematical identities, which include expressions that look different but generally act the same.
Lesson Outcomes
At the end of this lesson you will be able to
- verify a trigonometric identity graphically and numerically
- determine non-permissible values for a trigonometric identity
- use the reciprocal, quotient, and Pythagorean identities to simplify an expression
- explain the difference between an identity and an equation
Lesson Questions
In this lesson you will investigate the following questions:
- How can you determine whether or not an expression is a trigonometric identity?
- How can trigonometric identities be used to simplify problems?
Assessment
Your assessment may be based on a combination of the following tasks:
- completion of the Lesson 3 Assignment (Download the Lesson 3 Assignment and save it in your course folder now.)
- course folder submissions from Try This and Share activities
- additions to Glossary Terms and Formula Sheet
1.1. Launch
Module 5: Trigonometry Applications and Identities
Launch
Do you have the background knowledge and skills you need to complete this lesson successfully? Launch will help you find out.
Before beginning this lesson you should be able to
- define the cosecant, secant, and cotangent ratios
- determine non-permissible values for a trigonometric function
1.2. Are You Ready?
Module 5: Trigonometry Applications and Identities
Are You Ready?
Complete these questions. If you experience difficulty and need help, visit Refresher or contact your teacher.
- Rewrite each of the following using one of the three primary trigonometric ratios.
- Determine the values for which each of the following is undefined.
If you answered the Are You Ready? questions without difficulty, move to Discover.
If you found the Are You Ready? questions difficult, complete Refresher.
1.3. Refresher
Module 5: Trigonometry Applications and Identities
Refresher
Review the information on six common trigonometric ratios in Module 4, Lesson 4.
Go back to the Are You Ready? section and try the questions again. If you are still having difficulty, contact your teacher.
1.4. Discover
Module 5: Trigonometry Applications and Identities
Discover
Try This 1
- Use technology to plot the curve y = cos θ over the domain −2π ≤ θ ≤ 2π. Make a sketch of this function.
- Use technology to plot the curve y = sin θ cot θ over the domain −2π ≤ θ ≤ 2π. Make a sketch of this function.
- What do you notice about the two graphs?
- Although the graphs appear similar, they are not exactly the same. Complete sin θ cot θ Table to determine the difference. Multiply sin θ by cot θ to determine sin θ cot θ in the table.
![]() Save your answers in your course folder.
Save your answers in your course folder.
Share 1
With a partner or group, discuss the following questions based on the information in Try This 1.
- When is the statement cos θ = sin θ cot θ true?
- Predict all real values of θ for which the statement cos θ = sin θ cot θ is false.
- When they are defined, are cos θ and sin θ cot θ ever unequal?
![]() If required, save a record of your discussion in your course folder.
If required, save a record of your discussion in your course folder.
1.5. Explore
Module 5: Trigonometry Applications and Identities
Explore
In Try This 1 you saw that y = cos θ and y = sin θ cot θ have the same values when both functions are defined. cos θ = sin θ cot θ is an example of a trigonometric identity. A trigonometric identity is a trigonometric equation that is true for all permissible values of the variable in the expressions on both sides of the equation.1
You have already experienced a number of trigonometric identities so far in this course, including reciprocal and quotient identities. Think of how they got their names.
Reciprocal Identities |
||
|
|
|
Quotient Identities |
|
|
|
It is often possible to predict whether a statement is an identity by verifying the statement numerically or graphically. Try This 2 explores this idea.
Try This 2
Consider the following equations:
![]()
- Do you expect either of the equations to be a trigonometric identity? Explain.
- Determine the non-permissible values for each equation.

- Attempt to verify each potential identity by checking that both 40° and
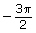 are solutions.
are solutions. 
- If you were to plot
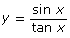 and y = cos x on the same graph and then plot
and y = cos x on the same graph and then plot 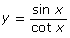 and y = cos x on the same graph, which two graphs would you expect to overlap one another?
and y = cos x on the same graph, which two graphs would you expect to overlap one another? - Plot the graphs in question 4 for domain −2π ≤ θ ≤ 2π. Was your prediction from question 4 correct?
![]() Save your answers in your course folder.
Save your answers in your course folder.
Share 2
With a partner or group, discuss the following questions based on your answers from Try This 2.
- Explain which of the two equations from Try This 2 you think is an identity.
- Looking back at the definition for a trigonometric identity and using the information in Try This 2, is it possible to be sure the equation is an identity? Explain.
![]() If required, save a record of your discussion in your course folder.
If required, save a record of your discussion in your course folder.
1 Source: Pre-Calculus 12. Whitby, ON: McGraw-Hill Ryerson, 2011. Reproduced with permission.
1.6. Explore 2
Module 5: Trigonometry Applications and Identities
In Try This 2 you checked an identity by showing that particular values make the identity true and that the expressions on both sides of the equal sign appear to have the same graphs. This check is called a verification. A verification does not prove that an equation is an identity because it is not possible to verify a trigonometric equation for every possible value.
To see an example of a verification, read “Example 1” on pages 291 to 293 of the textbook.
Self-Check 1
![]()
- Complete “Your Turn” from “Example 1” on page 293 of the textbook. Answer
- Complete questions 1, 2, and 5 on page 296 of the textbook. Answer
In Try This 2 you saw it was possible to verify an identity both graphically and numerically. In the next section you will use identities to simplify an expression.
Try This 3
Consider the expression
![]()
-
Determine non-permissible values for the expression.

- Use the reciprocal and quotient identities to simplify the expression to a single trigonometric function.

- Pick a permissible value of θ. Check that the original expression and the simplified expression are equal for this value.
- Use technology to graph both the original and simplified expressions.
![]() Save your answers in your course folder.
Save your answers in your course folder.
Share 3
With a partner or group, discuss the following questions based on your answers from Try This 3.
- What restrictions need to be placed on your simplified version of
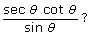
- Why is it necessary to include these restrictions?
- If you write that the simplified expression equals the original expression, is this an identity? Explain.
![]() If required, save a record of your discussion in your course folder.
If required, save a record of your discussion in your course folder.
1.7. Explore 3
Module 5: Trigonometry Applications and Identities
In Try This 3 you may have noticed that identities can be used to simplify expressions. A possible solution for Try This 3 is shown in Simplifying a Trigonometric Expression.
If you would like to see another example of using trigonometric identities to simplify expressions, read “Example 2” on pages 293 and 294 of the textbook. If you don't think you need to see another example, move ahead to Self-Check 2.
Self-Check 2
![]()
- Complete “Your Turn” from “Example 2” on page 294 of the textbook. Answer
- Complete questions 3, 4.a., and 4.b. on page 296 of the textbook. Answer
So far you have seen how to verify an identity and how to use identities to simplify expressions. In the next section, you will attempt to predict an identity beginning with a geometric representation.
Try This 4
From Module 4, you know that a point where the terminal arm of angle θ intersects the unit circle can be represented by (cos θ, sin θ), as shown in the diagram.
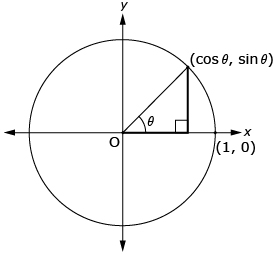
- Sketch the diagram shown and label the length of each side of the triangle.
- Use the Pythagorean theorem, a2 + b2 = c2, to predict a relationship between sine and cosine.

- Verify your prediction numerically and graphically.

- The identities 1 + tan2 θ = sec2 θ and 1 + cot2 θ = csc2 θ can also be predicted from a geometric representation similar to the one shown.
- Verify 1 + cot2 θ = csc2 θ numerically and graphically.
- Multiply each term in 1 + tan2 θ = sec2 θ by cos2 θ and simplify. What do you notice?
![]() Save your answers in your course folder.
Save your answers in your course folder.
1.8. Explore 4
Module 5: Trigonometry Applications and Identities
In Try This 4 you may have found that sin θ and cos θ are related by the identity sin2 θ + cos2 θ = 1 by drawing a diagram similar to the diagram shown. You also saw that 1 + tan2 θ = sec2 θ and 1 + cot2 θ = csc2 θ. As such, they are identities. These are called Pythagorean identities because each can be derived from the Pythagorean theorem, a2 + b2 = c2.
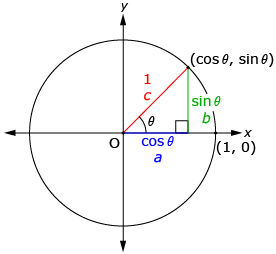
Watch “Pythagorean Identity Derivation” to see another derivation of these identities.
Read “Example 3” on page 295 of the textbook. Pay attention to how the identity is verified numerically.
Self-Check 3
- Complete the activity in “Simplifying Trigonometric Expressions."
![]()
- Complete questions 4.c., 7, 11, 13, and 14 on pages 296 to 298 of the textbook. Answer
1.9. Explore 5
Module 5: Trigonometry Applications and Identities
Add the following terms to your copy of Glossary Terms:
- verification
- trigonometric identity
- reciprocal identity
- quotient identity
- Pythagorean identity
Add the following formulas to your copy of Formula Sheet:
- sin2 θ + cos2 θ = 1
- 1 + tan2 θ = sec2 θ
- 1 + cot2 θ = csc2 θ
1.10. Connect
Module 5: Trigonometry Applications and Identities
Complete the Lesson 3 Assignment that you saved in your course folder at the beginning of this lesson. Show work to support your answers.
![]() Save your responses in your course folder.
Save your responses in your course folder.
Project Connection
There is no Project Connection in this lesson.
1.11. Lesson 3 Summary
Module 5: Trigonometry Applications and Identities
Lesson 3 Summary

Photos.com/Thinkstock
In Focus you read about two race cars that were identical in every way other than colour. This analogy was used to describe trigonometric identities, equations with sides that look different but generally act the same. An identity is a mathematical equation that is true for any permissible value. In this lesson you worked with Pythagorean and reciprocal identities as well as some other less common identities. It is possible to verify an identity both graphically and numerically when given a potential identity.
Identities can be used to simplify some expressions; if one side of the identity appears in an expression, the other side of the identity can replace it. When simplifying using an identity, any restrictions on the identity also apply to the simplified expression.
In the next lesson you will learn some new trigonometric identities and use identities to help solve trigonometric equations.