Lesson 5
| Site: | MoodleHUB.ca 🍁 |
| Course: | Math 30-1 SS |
| Book: | Lesson 5 |
| Printed by: | Guest user |
| Date: | Tuesday, 9 December 2025, 10:35 PM |
Description
Created by IMSreader
1. Lesson 5
Module 5: Trigonometry Applications and Identities
Lesson 5: Proving Trigonometric Identities
Focus

iStockphoto/Thinkstock
When a person decides to buy a vehicle, or a mechanic needs to fix a vehicle, that person will often reference the technical specifications for that vehicle. Specifications give details of things like vehicle size, parts, cost, and performance. But before the specifications are written, the car must go through a design process. Engineers spend a lot of time and thought trying to make the car appealing and functional.
An identity is like the specifications of a vehicle. An identity is a ready tool that a user can expect to give reliable information without a lot of thought. Just like a car must be designed before the specifics can be used, an identity must be proven before the identiry is used; the identity must go through a testing procedure to show it will always work properly. This testing procedure is called a proof.

Hemera/Thinkstock
Lesson Outcome
At the end of this lesson you will be able to prove a trigonometric identity.
Lesson Questions
In this lesson you will investigate the following questions:
- How can a trigonometric identity be proven?
- Why is it necessary to prove an identity?
Assessment
Your assessment may be based on a combination of the following tasks:
- completion of the Lesson 5 Assignment (Download the Lesson 5 Assignment and save it in your course folder now.)
- course folder submissions from Try This and Share activities
- additions to Glossary Terms
- work under Project Connection
1.1. Discover
Module 5: Trigonometry Applications and Identities
Discover
Try This 1
Consider the possible identity ![]() = x + 150.
= x + 150.
- Verify
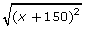 = x + 150 for x = −81, 0, and 176.
= x + 150 for x = −81, 0, and 176. - Verify
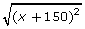 = x + 150 graphically for −10 < x < 10.
= x + 150 graphically for −10 < x < 10. - Is
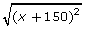 = x + 150 an identity?
= x + 150 an identity? - Try using x = −200 to verify
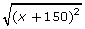 = x + 150. Does your answer to question 3 change?
= x + 150. Does your answer to question 3 change?
![]() Save your answers in your course folder.
Save your answers in your course folder.
Share 1
With a partner or group, discuss the following questions based on Try This 1.
- What limitations are there to verifying an identity numerically or graphically?
- It would be impossible to verify an identity like this for all possible inputs. How could you determine whether an identity is true for all defined values?
![]() If required, save a record of your discussion in your course folder.
If required, save a record of your discussion in your course folder.
1.2. Explore
Module 5: Trigonometry Applications and Identities
Explore
In Try This 1 you saw there are limitations to verifying an identity numerically and graphically. It is impossible to test every possible value for the variable in most potential identities. This leads to the idea of a mathematical proof. A proof is an argument that shows how you know a statement is true. The statement is called a theorem once the statement has been proven. The theorem can then be used to solve problems or prove other statements. Complete Try This 2 to explore the proof of a trigonometric identity.
Try This 2
Consider the potential identity ![]() .
.
- Determine the non-permissible values for the potential identity.


-
- Verify the identity for
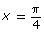 and −1.5.
and −1.5. - Verify the identity graphically.
- Verify the identity for
- Show that
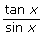 simplifies to
simplifies to 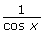 .
. - Show that sec x simplifies to
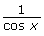 .
.
The answers to questions 3 and 4 together are a proof of the identity ![]() = sec x for all permissible values. This means you know
= sec x for all permissible values. This means you know ![]() is true for all permissible values of x.
is true for all permissible values of x.
- Try to solve
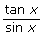 = sec x for x. What do you notice?
= sec x for x. What do you notice?
![]() Save your answers in your course folder.
Save your answers in your course folder.
Share 2
With a partner or group, discuss the following questions based on the information from Try This 2.
- When is the identity
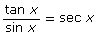 valid?
valid? - Why do the answers to questions 3 and 4 of Try This 2 prove that
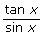 = sec x is an identity?
= sec x is an identity? - Why doesn’t the answer to question 5 of Try This 2 prove that
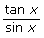 = sec x is an identity?
= sec x is an identity?
1.3. Explore 2
Module 5: Trigonometry Applications and Identities
In Try This 2 you showed that it is possible to express each side of ![]() in the equivalent form
in the equivalent form ![]() Reducing each side to a common expression is a common style of proof used for trigonometric identities. In question 5 of Try This 2, you tried to solve the equation
Reducing each side to a common expression is a common style of proof used for trigonometric identities. In question 5 of Try This 2, you tried to solve the equation ![]() and probably reduced it to something like 1 = 1 or 0 = 0.
and probably reduced it to something like 1 = 1 or 0 = 0.
Although solving an identity gives a true statement, this is not a proof. Consider the equation ![]() from the beginning of the lesson. It is also possible to simplify this to something true, but you know it is not an identity because
from the beginning of the lesson. It is also possible to simplify this to something true, but you know it is not an identity because ![]() reduces to |x + 150|, not x + 150.
reduces to |x + 150|, not x + 150.
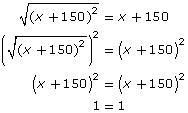
Read “Example 1” on pages 310 and 311 of the textbook to see a comparison of verifying an identity and proving an identity.
Self-Check 1
Complete “Your Turn” from “Example 1” on page 311 of the textbook. Answer
1.4. Explore 3
Module 5: Trigonometry Applications and Identities
Proving an identity does not follow a set pattern; each proof is unique. Here are some strategies that may be useful.
- Only manipulate one side at a time.
- Begin with the more complex side; it is often easier to simplify than to expand.
- Use known identities to make substitutions.
- Try changing all trigonometric ratios to sines and cosines.
- When second-degree trigonometric functions are used (sin2 x, tan2 x), consider Pythagorean identities.
- When the inputs for the functions are different (cos 2x, cos x), consider double-angle, sum, or difference identities.
- Try factoring an expression.
- Try expanding an expression.
- If fractions are used, try writing each side as a single fraction.
- Try multiplying the numerator and denominator by the conjugate of an expression. This can be helpful if 1 ± sin x or 1 ± cos x appears as part of a fraction. (The conjugate of A + B is A − B.)
The most important suggestion of all is DON’T GIVE UP. You will rarely write a proof correctly on your first try. Proving an identity will often require multiple attempts, a lot of scrap paper, and a bit of luck—none of which are shown in examples of proofs. Be patient.
Complete Try This 3 with a group if possible, but alone if necessary.
Try This 3
Consider the identity csc x(1 + sin x) = 1 + csc x.
- What values of x are not permissible for this identity?
- Which strategies do you think may be used to prove the identity?

- Try using one or more of the strategies you discussed in question 2 to prove the identity.
-
How many different proofs are possible? Explain.
-
How do you know when you are finished a proof?
![]() Save your responses in your course folder.
Save your responses in your course folder.
Share 3
Compare your proof to the proofs of other students. Your comparisons can include considerations like length, difficulty, clarity, and the strategy used.
![]() If required, save your responses and a record of your discussion in your course folder.
If required, save your responses and a record of your discussion in your course folder.
Review the list of strategies provided just before Try This 3.
1.5. Explore 4
Module 5: Trigonometry Applications and Identities
There are many different ways of writing the proof of an identity correctly; however, the proof style used in this lesson always ends with the left side the same as the right side. Two possible proofs are shown in Example Proof 1A and Example Proof 1B. Compare these proofs to your proof.


Self-Check 2
Complete question 2 on page 314 of the textbook. Answer
The next identity has double angles in it. Complete Try This 4 with a group if possible, but alone if necessary.
Try This 4
Consider the identity ![]() .
.
- Which side of the equation do you feel is more complex?
- Which strategies do you think may be used to prove the identity?

-
Try using one or more of the strategies you discussed in question 2 to prove the identity.
-
Compare your proof to a partner’s.
- Compare your proof from Try This 4 to Example Proof 2.
![]() Save your responses and a record of your discussion in your course folder.
Save your responses and a record of your discussion in your course folder.
Remember, there are many correct ways to write a proof.
Review the list of strategies provided just before Try This 3.
1.6. Explore 5
Module 5: Trigonometry Applications and Identities
Self-Check 3
![]()
- Complete “Your Turn” from “Example 2” on pages 311 and 312 of the textbook. Answer
- Complete questions 7.a., 8, 10.a., 11.a., and 13 on pages 314 and 315 of the textbook. Answer
The following identity is a bit harder to prove if you don’t see a particular step. Complete Try This 5 with a group if possible, but alone if necessary.
Try This 5
Consider the identity ![]() .
.
- Determine the non-permissible values for the identity.
- Which strategies do you think will be useful when trying to prove this identity?

-
Prove the identity.
- When is it useful to multiply the numerator and denominator of a fraction by a conjugate?
![]() Save your responses and a record of your discussion in your course folder.
Save your responses and a record of your discussion in your course folder.
Share 4
Compare your proof to the proofs of other students. Your comparison can include considerations like length, difficulty, clarity, and the strategy used.
![]() If required, save your responses and a record of your discussion in your course folder.
If required, save your responses and a record of your discussion in your course folder.
Review the list of strategies provided just before Try This 3.
1.7. Explore 6
Module 5: Trigonometry Applications and Identities
![]()
- Complete “Your Turn” from “Example 4” on page 313 of the textbook. Answer
- Complete questions 3.b., 3.c., 10.b., 10.c., and 15 on pages 314 and 315 ofthe textbook. Answer
Add the following terms to your copy of Glossary Terms:
- mathematical proof
- theorem
1.8. Connect
Module 5: Trigonometry Applications and Identities
Complete the Lesson 5 Assignment that you saved in your course folder at the beginning of this lesson. Show work to support your answers.
![]() Save your responses in your course folder.
Save your responses in your course folder.
Project Connection
You are now ready to apply your understanding of proving trigonometric identities. Go to Module 5 Project: Pushing the Limits of Vehicle Performance and complete Activity 2: Part 2. Complete any remaining parts of your project.
![]() Save your responses in your course folder. Submit your completed Module 5 Project to your teacher.
Save your responses in your course folder. Submit your completed Module 5 Project to your teacher.
Going Beyond

top left: iStockphoto/Thinkstock; top right: Hemera/Thinkstock;
bottom left: iStockphoto/Thinkstock;
bottom right: iStockphoto/Thinkstock
Mathematics is a critical part of human creativity. Like art, mathematics has its own structure, logic, and meaning. Like music, mathematics has harmony and dissonance. Like literature, mathematics has metaphor, ambiguity, and mystery. It has history. Mathematics has a sense of outcome and a feeling of rightness.
Mathematics possesses not only precision, but beauty, especially in the form of an elegant proof. Your experience with this lesson tells you that there are many ways to complete a proof, so what makes one proof ordinary and another elegant?
An elegant proof
- uses a minimum of assumptions
- is unusually succinct
- derives a result in a surprising way
- is based on new and original insights
- can be easily generalized to solve a family of similar problems
Care needs to be taken when reading proofs. It is often possible to follow flawed logic to an absurd conclusion. Consider the following, which claims to prove that 2 = 1.
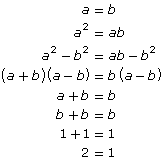
Comment on the validity of this “proof.”
1.9. Lesson 5 Summary
Module 5: Trigonometry Applications and Identities
Lesson 5 Summary
In this lesson you learned about mathematical proofs, which are at the core of mathematics. A proof is just an argument showing that a statement must be true. Once you know the statement is always true, you can use the statement in future scenarios, such as simplifying expressions and solving other equations.
For the type of proof you learned in this lesson, the goal is to show that both sides of the identity are equal by manipulating each side independently until they are the same expression. There is no specific pattern for how to proceed with a given proof. A bit of luck, determination, and some intuition will help you complete a proof.
In the next module you will begin to explore exponents and their inverse, logarithms.