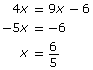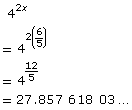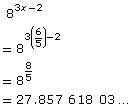Lesson 2
| Site: | MoodleHUB.ca 🍁 |
| Course: | Math 30-1 SS |
| Book: | Lesson 2 |
| Printed by: | Guest user |
| Date: | Tuesday, 9 December 2025, 11:17 PM |
Description
Created by IMSreader
1. Lesson 2
Module 6: Exponents and Logarithms
Lesson 2: Exponential Equations
Focus

iStockphoto/Thinkstock
Are you saving money for something special? People save money for many reasons, like for a new computer, post-secondary school, a new car, or a home. People can invest money in a bank or investment firm. You can calculate how much money you will save using formulas based on exponential equations.
In Lesson 1 you looked at graphing exponential functions. In this lesson you will look at how to solve exponential equations.
Lesson Outcomes
At the end of this lesson you will be able to
- determine the solution of an exponential equation in which the bases are powers of one another
- solve problems that involve loans, mortgages, and investments
Lesson Question
You will investigate the following question:
- How can exponential equations be used to solve problems involving growth and decay?
Assessment
Your assessment may be based on a combination of the following tasks:
- completion of the Lesson 2 Assignment (Download the Lesson 2 Assignment and save it in your course folder now.)
- course folder submissions from Try This and Share activities
- additions to Glossary Terms
1.1. Launch
Module 6: Exponents and Logarithms
Launch
Do you have the background knowledge and skills you need to complete this lesson successfully? Launch will help you find out.
Before beginning this lesson you should be able to
- simplify exponential expressions using exponent laws
- express values with base 2 or base 3
1.2. Are You Ready?
Module 6: Exponents and Logarithms
Are You Ready?
Complete the following questions. If you experience difficulty and need help, visit Refresher or contact your teacher.
- Simplify the following expressions, leaving the answer with positive exponents.
- Express each value as a power with base 2.
- Express each value as a power with base 3.
If you answered the Are You Ready? questions without difficulty, move to Discover.
If you found the Are You Ready? questions difficult, complete Refresher.
1.3. Refresher
Module 6: Exponents and Logarithms
Refresher
Use Exploring Laws of Exponents to review the exponent laws. Click on each of the exponent laws.
Review evaluating exponential expressions in “Exponent Rules 2.”
Go back to the Are You Ready? section and try the questions again. If you are still having difficulty, contact your teacher.
1.4. Discover
Module 6: Exponents and Logarithms
Discover
Try This 1
- Complete a table similar to the one shown by substituting the value of n into each exponential expression. Use your knowledge of exponent laws to rewrite each expression as a power with base 2.
n
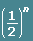
2n
4n
−2
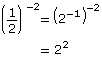
−1
0
1
2
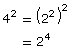
- For each exponential expression in the column for 2n, find the equivalent expression in the other columns.1
![]() Save your responses in your course folder.
Save your responses in your course folder.
Share 1
With a partner or group, discuss the following question based on your responses to Try This 1:
When you are given two exponential expressions, how can you determine if the expressions are equivalent?
![]() If required, save a record of your discussion in your course folder.
If required, save a record of your discussion in your course folder.
1 Adapted from Pre-Calculus 12. Whitby, ON: McGraw-Hill Ryerson, 2011. Reproduced with permission.
1.5. Explore
Module 6: Exponents and Logarithms
Explore
In Discover you rearranged exponential expressions to have the same base. For example, you may have found the following equivalent expression:
![]()
By rewriting all three expressions as base 2, you can see the expressions are all identical.
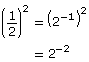
In Try This 1 you were changing the base of the powers so they were all base 2. In this lesson you will be changing powers to a different base. To do this you will have to use your knowledge of powers. For example, 64 can be written as base 2, base 4, or base 8.
If you are unsure of the exponent, you can check using your calculator.
To see an example of how to change the base of powers, read “Example 1” on page 360 of the textbook. Notice how laws of powers are used to simplify each expression.
Rewriting expressions with a common base allows you to compare the expressions and find equivalent expressions. It is very difficult to compare exponential expressions if they do not have the same base. Keep this important idea in mind as you complete Try This 2.
Try This 2
- Solve the equation 2x = 8 algebraically for x. Describe how you determined the value of x.

- Apply the method you used in question 1 to solve the following equations. For each equation, describe how you solved for the value of x.

- Solve for x in the equation 2x − 1 = 8.
- Solve for x in the equation 2x = 8x − 1.
![]() Save your responses in your course folder.
Save your responses in your course folder.
Share 2
With a partner or group, discuss the following question based on your solutions in Try This 2:
Describe the methods you used to solve for x. Did you use the same method for each question? Why or why not? Do you need a more efficient method to solve these questions?
![]() If required, save a record of your discussion in your course folder.
If required, save a record of your discussion in your course folder.
1.6. Explore 2
Module 6: Exponents and Logarithms
In Try This 2 you were working with exponential equations. 2x = 8x−1 is an exponential equation because the equation has a variable, x, in the exponent.
In Discover you may have changed the bases in an expression so they were the same on each side. This helped you compare and determine if the expressions were equal. You may have used a similar strategy to solve the exponential equations in Try This 2.
When the bases are the same on each side of an equation, the exponents on each side of the equation must be equal. This can be expressed by the property that if bx = by, then x = y and b ≠ −1, 0, 1.
For example, in Try This 2 you solved 2x = 8x−1.

To use this property to solve exponential equations, there must be only one power on each side of the equation and the bases of each power must be the same. At times, the exponent laws may need to be used to change the base of a power.
Read “Example 2” part a on page 360 of the textbook. Notice that two methods are shown. Method 1 solves the equation by changing bases, and Method 2 uses graphing to solve the equation. Solving exponential equations using a graphical method is valid, but the focus for this lesson is on using an algebraic approach to solve exponential equations.
Self-Check 1
- Complete “Your Turn” at the end of “Example 1” on page 360 of the textbook. Answer
- Complete “Your Turn” part a at the end of “Example 2” on page 361 of the textbook. Answer
- Complete question 4.c. on page 364 of the textbook. Answer
- Refer to the property, if bx = by, then x = y and b ≠ −1, 0, 1. Explain why there is a restriction that b ≠ −1, 0, 1. Answer
1.7. Explore 3
Module 6: Exponents and Logarithms
In Self-Check 1 you practised changing the base of a power. In Try This 3 you will try to use this skill to solve exponential equations.
Try This 3
Complete the following questions to solve the equation 42x = 83x−2.
- How can you write 4 and 8 as powers with the same base?

- Write 42x as a power with the base you chose in question 1. What exponent law did you use to simplify the expression?
- Write 83x−2 as a power with the base you chose in question 1. What exponent law did you use to simplify the expression?
- Equate your answers from questions 2 and 3. Since both sides of the equation are single powers with the same base, the exponents must be equal. Set the exponents equal to each other and solve for x.
- Check if your answer is correct.

- Use a graphical method to solve the equation 42x = 83x−2. Describe the process you used.
![]() Save your responses in your course folder.
Save your responses in your course folder.
1.8. Explore 4
Module 6: Exponents and Logarithms
Your work from Try This 3 might have looked something like this:
42x = 83x−2 |
|
||||||
(22)2x = (23)3x−2 |
Change 4 and 8 to a powers with base 2. |
||||||
|
Apply the power of a power exponent law and multiply the exponents together. Don’t forget to use the distributive property when multiplying a binomial. |
||||||
|
There is a single power on each side of the equation. The exponents are equal. |
||||||
|
Verify. You could substitute the value for x into the original equation to check your solution. |
||||||
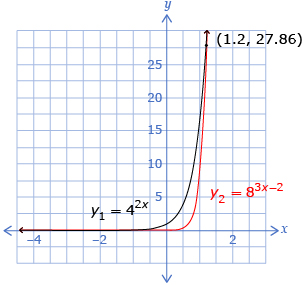 |
You could use a graphical method to determine the value of x.
The x-value of the intersection point is 1.2, so the solution is x = 1.2, or |
||||||

Jupiterimages/Comstock/Thinkstock
You may remember from Lesson 1 that radioactive material decay is measured in half-life. Half-life is the amount of time it takes for half of a radioactive material to decay. In the example Solving an Exponential Equation, the half-life of Sodium-24 is used to find out how long it will take for the material decay to ![]() of its original mass. In order to find the solution, powers will be changed to the same bases. Notice how there are two choices as to what base can be used.
of its original mass. In order to find the solution, powers will be changed to the same bases. Notice how there are two choices as to what base can be used.
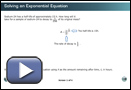
When entering powers into your calculator, use brackets around the exponent. For example, to enter 32x−3 into your calculator, type 3, ^(this is the exponent button), bracket, 2x − 3, bracket.
Self-Check 2
![]()
- Complete “Your Turn” part b at the end of “Example 2” on page 361 of the textbook. Answer
- Complete question 9 on page 364 of the textbook. Answer
- Complete question C2 on page 365 of the textbook. Answer
In Try This 3 you solved an exponential equation where the base of each power could be expressed with a common base. How would you solve an equation where a common base could not be found?
Try This 4
- The exponential equation 3x = 4 cannot be solved using the method used in Try This 3. Why is this?
- Try different strategies to solve the equation. Verify the solution of each strategy by substitution.
![]() Save your responses in your course folder.
Save your responses in your course folder.
1.9. Explore 5
Module 6: Exponents and Logarithms
You may have used a guess-and-check strategy or even a graphing strategy to find the solution to Try This 4. The following example problem, Compound Interest with Different Bases, uses both strategies. Compare these to the method you used to solve Try This 4.
In future lessons you will explore another method used to solve exponential equations with different bases.
Self-Check 3
![]()
- Complete question 6.d. on page 364 of the textbook. Answer
- Complete “Your Turn” at the end of “Example 3” on page 363 of the textbook. Answer
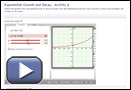
- Complete questions 1 to 5 in “Exponential Growth and Decay - Activity A.”
Add exponential equation to your copy of Glossary Terms.
1.10. Connect
Module 6: Exponents and Logarithms
Complete the Lesson 2 Assignment that you saved in your course folder at the beginning of the lesson. Show work to support your answers.
![]() Save your responses in your course folder.
Save your responses in your course folder.
Project Connection
There is no Project Connection in this lesson.
1.11. Lesson 2 Summary
Module 6: Exponents and Logarithms
Lesson 2 Summary

iStockphoto/Thinkstock
In this lesson you explored how to solve exponential equations.
You learned that when there is a single power on each side of the equal sign and the bases are the same, the exponents are equal. You needed to change the bases of the powers to a common base for some questions.
Another method was to guess and check. This method was useful when the bases could not be changed to a common base.
You can use substitution or graphing to check or verify your solution.
You explored how the compound interest formula could be used to determine how long you would need to invest money in order to have the money grow to a certain amount.
In future lessons you will learn an algebraic method for solving exponential equations when the bases do not share a common base.