Lesson 5
| Site: | MoodleHUB.ca 🍁 |
| Course: | Math 30-1 SS |
| Book: | Lesson 5 |
| Printed by: | Guest user |
| Date: | Tuesday, 9 September 2025, 3:03 PM |
Description
Created by IMSreader
1. Lesson 5
Module 6: Exponents and Logarithms
Lesson 5: Laws of Logarithms
Focus
iStockphoto/Thinkstock
In this module you have learned about logarithms and how they relate to an exponential expression. In the past, you have worked with expressions that have more than one power. You have used the laws of powers to simplify multiple powers in an expression. Do you think there are laws of logarithms that can be used to simplify an expression with multiple logarithms? How would these be related to the laws of powers?
Logarithmic scales are helpful when working with values that are very large or very small. In the case of the pH scale, the values are very small. How can taking the logarithm of a value help determine the pH of a substance?
Lesson Outcomes
At the end of this lesson you will be able to
- demonstrate an understanding of the product, quotient, and power laws of logarithms
- apply the laws of logarithms to determine equivalent logarithmic expressions
Lesson Question
You will investigate the following question:
- How can the product, quotient, and power laws of logarithms be applied?
Assessment
Your assessment may be based on a combination of the following tasks:
- completion of the Lesson 5 Assignment (Download the Lesson 5 Assignment and save it in your course folder now.)
- course folder submissions from Try This and Share activities
- additions to Formula Sheet
- work under Project Connection
1.1. Launch
Module 6: Exponents and Logarithms
Launch
Do you have the background knowledge and skills you need to complete this lesson successfully? Launch will help you find out.
Before beginning this lesson you should be able to
- change radicals to powers with rational exponents and vice versa
- solve inequalities
1.2. Are You Ready?
Module 6: Exponents and Logarithms
Are You Ready?
Complete the following questions. If you experience difficulty and need help, visit Refresher or contact your teacher.
- Write the following expressions as powers with rational exponents and simplify where possible.
- Write the following expressions as radicals.
-
Solve the following inequalities.
If you answered the Are You Ready? questions without difficulty, move to Discover.
If you found the Are You Ready? questions difficult, complete Refresher.
1.3. Refresher
Module 6: Exponents and Logarithms
Refresher
Source: Khan Academy
(
BY-NC-SA 3.0)
Watch “Rational Exponents and Exponent Laws” for an example of changing a radical to a power.
Source: Khan Academy
( BY-NC-SA 3.0)
Watch “Radical Equivalent to Rational Exponents” for an example of expressing a power as a radical.
Source: Khan Academy
( BY-NC-SA 3.0)
View “Solving Inequalities” for an example of solving a linear inequality.
Review how to solve quadratic inequalities in Mathematics 20-1 Learn EveryWare Module 4 Lesson 8 Summary.
Go back to the Are You Ready? section and try the questions again. If you are still having difficulty, contact your teacher.
1.4. Discover
Module 6: Exponents and Logarithms
Discover
In previous lessons you simplified exponential expressions by applying the exponent laws. In this lesson you will see how the exponent laws can be related to logarithms.
Try This 1
Complete “Investigate the Laws of Logarithms” questions 1 to 3 on pages 392 to 393 of the textbook.
Save your responses in your course folder.
Share 1
With a partner or group, discuss question 5 on page 393 of the textbook based on your responses in Try This 1.
If required, save a record of your discussion in your course folder.
1.5. Explore
Module 6: Exponents and Logarithms
Explore
In Try This 1 you may have determined the following patterns. They are called the laws of logarithms.
LAWS OF LOGARITHMS |
||
Law of Logarithms |
Law Expressed Mathematically |
Comparison Between Law of Logarithm and Law of Powers |
Product Law of Logarithms |
logb (M × N) = logb M + logb N |
(bm)(bn) = bm+n
logb (M × N) = logb M + logb N
Note that multiplying terms in a logarithm or powers is equal to the sum of the logarithms or exponents. |
Quotient Law of Logarithms |
|
Note that dividing terms in a logarithm or powers is equal to the difference between the logarithms or exponents. |
Power Law of Logarithms |
logb (Mn) = nlogb M |
logb (Mn) = nlogb M
Note that a power in a logarithm or a power to a power is equal to the product of the power and the logarithm or the exponents of the power. |
Open Properties of Logarithms to see how the laws of logarithms can be derived. Choose the Tutorial button (
), and then select The Product Law of Logarithms. Work your way through the activities.
1.6. Explore 2
Module 6: Exponents and Logarithms
To see the proofs of the product, quotient, and power laws of logarithms, read “Link the Ideas” on pages 394 to 395 of the textbook. Notice how each logarithmic law is proved using the exponent laws.
In Try This 2 you will look at using the laws of logarithms to evaluate an expression.
iStockphoto/Thinkstock
Try This 2
Evaluate the expression 
using the laws of logarithms.
- Write
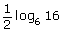as a logarithm with no coefficient. 
- Write log6 18 − log6 2 as a single logarithm.
- Use your answers from questions 1 and 2 to write the original expression as a single logarithm, and then simplify the expression.
- Try to evaluate
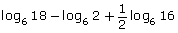using your calculator. Can this be easily done on your calculator? If you did use your calculator, did you get the same answer?
To enter logarithms into your calculator, use the LOG button. Some calculators let you enter the base of the logarithm using this button. For other calculators, the LOG button is the common logarithm with base 10. On these calculators, to enter log2 8, you need to use the change-of-base identity for logarithms. The identity states
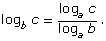
To write log2 8 as a logarithm of base 10, the expressions would become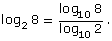
On your calculator you would enter LOG (8) ÷ LOG (2). Remember, when no base is indicated, it is assumed to be base 10.
Save your responses in your course folder.
1.7. Explore 3
Module 6: Exponents and Logarithms
In Try This 2 you used laws of logarithms to determine the value of a logarithmic expression. You may have simplified the logarithmic expression 
using the following process:
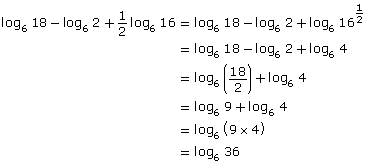
Rewrite log6 36 in exponent form to solve.
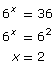
Therefore 
On some calculators it is easy to enter this expression to determine the value. On other calculators it takes longer to enter and it may be easier to evaluate using the laws of logarithms.
For another example, read “Example 2” on page 396 of the textbook.
Self-Check 1
1.8. Explore 4
Module 6: Exponents and Logarithms
In Try This 2 you used the laws of logarithms to simplify logarithms of numbers. Could the laws of logarithms be applied to logarithmic expressions with variables?
Try This 3
-
- Use the laws of logarithms to expand the expression
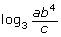, and write it in terms of individual logarithms. - Explain the process used and the laws of logarithms you used.
- Use the laws of logarithms to expand the expression
-
- Write the expression
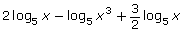as a single logarithm. - Explain the process used and the laws of logarithms you used.
- State any restriction on the variable.
- Write the expression
- How are the processes used in questions 1 and 2 similar or different?
Save your responses in your course folder.
1.9. Explore 5
Module 6: Exponents and Logarithms
In Try This 3 you looked at expanding and simplifying logarithmic expressions. You may have expanded the expression as follows:
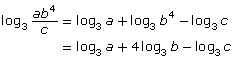
You may have simplified the expression as follows:
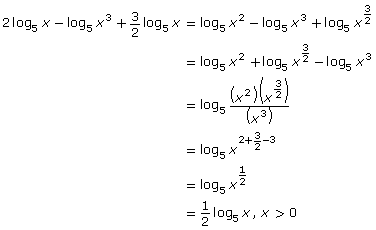
Remember, expressions of the form log x are only defined for x > 0.
Read “Example 1” on page 395 of the textbook. As you read through the example, determine whether the order in which you apply the different laws of logarithms would change the solution.
Read “Example 3” on page 397 of the textbook. Notice how inequalities are set up to determine the restrictions on x. If you need to review how to solve quadratic inequalities, see the Refresher section of this lesson.
Carefully follow the laws of logarithms used in this lesson.
For example,
log (x + y) ≠ log x + log y; instead, log x + log y = log (xy)
(log x)(log y) ≠ log(xy); instead, log(xy) = log x + log y
Self-Check 2
1.10. Explore 6
Module 6: Exponents and Logarithms
You have practised using the laws of logarithms to simplify expressions. You can also use the laws to help you simplify problems. In Try This 4 you will use what you have learned to solve a problem with a logarithmic scale.
Try This 4
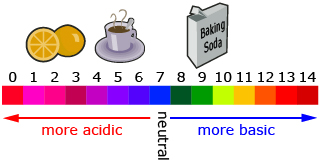
The pH scale is a logarithmic scale that is used to communicate the acidity or alkalinity of a solution. To determine the pH of a solution, the equation used is pH = − log [H+], where [H+] is the concentration of hydrogen ions measured in moles per litre (mol/L). The square brackets around [H+] indicate concentration. Refer to the image to see pH values for some common substances. Also make note of the pH values that describe acidic, neutral, and basic substances.
- What would be the pH of vinegar that has the following concentration of hydrogen ions: [H+] = 0.006 31 mol/L.
- Coffee has a pH of 5.4. How many times as acidic as coffee is vinegar?
- A lemon-flavoured pop has a pH of 2.8. A cola-flavoured pop is 3 times as acidic as the lemon-flavoured pop. What is the pH of the cola-flavoured pop?
Save your responses in your course folder.
Logarithmic scales are useful when you have a very large range of values. In the pH scale, the concentration of hydrogen ions has a very large range between solutions. Many logarithmic scales are base 10, so this means that an increase of 1 on the scale is actually a factor of 10. For example, a pH of 4 is 10 times more acidic than a pH of 5.
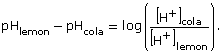
1.11. Explore 7
Module 6: Exponents and Logarithms
© Schlierner/37737907/Fotolia
Dr. Soren Sorensen (1868–1939) developed the pH scale to have a universal measurement of the acidity of solutions. There are different explanations of what the term pH represents, but some people believe that pH stands for power of hydrogen.
In Try This 4 you looked at the pH scale, which is another example of a logarithmic scale. View Solving pH Scale Problems to see a possible method that could be used to solve the questions in Try This 4.
The decibel scale is a logarithmic scale used to measure sound intensity. As you read through the following example, make note of the similarities and differences between this scale and the pH scale. Read “Example 4” on pages 398 to 399 of the textbook.
Self-Check 3
- Complete question 13 on page 401 of the textbook. Answer
- Complete question 16 on page 402 of the textbook. Answer
Add the following formulas to your copy of Formula Sheet.
- logb (M × N) = logb M + logb N
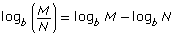
- logb (Mn) = nlogb M
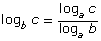
1.12. Connect
Module 6: Exponents and Logarithms
Complete the Lesson 5 Assignment that you saved in your course folder at the beginning of the lesson. Show work to support your answers.
Save your responses in your course folder.
Project Connection
You are ready to apply your understanding of the relationship between a function and the square root of the function. Go to Module 6 Project: Movie Money, and complete Part 2.
Save your responses in your course folder.
1.13. Lesson 5 Summary
Module 6: Exponents and Logarithms
Lesson 5 Summary
In this lesson you explored the laws of logarithms. You used numeric values to determine what the laws should be and, then, looked at how the laws could be derived. You studied the following laws:
- product law of logarithms:
logb (M × N) = logb M + logb N - quotient law of logarithms:
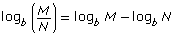
- power law of logarithms:
logb (Mn) = nlogb M
The laws of logarithms can be used to evaluate logarithmic expressions as well as expand or simplify logarithmic expressions.
You also saw how logarithmic scales are used. You solved problems involving the decibel scale and the pH scale.
Using the laws of logarithms to expand or simplify logarithmic expressions will be helpful in the next lesson. In Lesson 6 you will solve logarithmic equations.