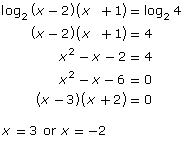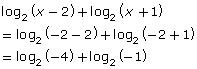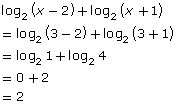Lesson 6
| Site: | MoodleHUB.ca 🍁 |
| Course: | Math 30-1 SS |
| Book: | Lesson 6 |
| Printed by: | Guest user |
| Date: | Monday, 8 September 2025, 8:22 PM |
Description
Created by IMSreader
1. Lesson 6
Module 6: Exponents and Logarithms
Lesson 6: Logarithmic and Exponential Equations
Focus
iStockphoto/Thinkstock
Do you have a savings account, RESP, or other type of investment? Do you enjoy watching your money grow and gain interest? If you have a car loan, credit card, or other borrowed money, you might have experienced interest in a different way! Whether you are calculating your interest on investments or your interest charges on loans, you will be using formulas that contain exponents.
In Lesson 2 you solved exponential equations in which the bases of the powers were the same and the exponents could be equated. When a common base of the powers could not be found, the equations were much more difficult to solve. How can you solve any exponential equation algebraically?
In this lesson you will explore how to solve equations that include logarithms and how logarithms will help solve exponential equations.
Lesson Outcomes
At the end of this lesson you will be able to
- solve logarithmic equations and verify the solution
- solve exponential equations when the bases are not powers of one another
- solve a problem by modelling a situation with an exponential or logarithmic equation
Lesson Question
You will investigate the following question:
- How can logarithmic or exponential equations be solved?
Assessment
Your assessment may be based on a combination of the following tasks:
- completion of the Lesson 6 Assignment (Download the Lesson 6 Assignment and save it in your course folder now.)
- course folder submissions from Try This and Share activities
- additions to Glossary Terms and Formula Sheet
- work under Project Connection
1.1. Discover
Module 6: Exponents and Logarithms
Discover
There are many applications of exponential and logarithmic functions. In most cases, the expressions in the equations are difficult to write in the same base, so you need to find a way to solve these equations algebraically. In Try This 1 you will review how to solve equations with the same base. Later in the lesson you will learn how to solve equations that can’t be easily rewritten with the same base.
Try This 1
Use the equation 2 log x = log 25 to answer the following questions.
- Apply the power law of logarithms to the left side of the equation.
- Explain how you can solve the resulting equation algebraically.
- Determine two values of x that satisfy the equation from question 2. Are both solutions valid?
- Describe how you can solve the equation graphically.
- Use your method to solve the equation graphically.1
Save your responses in your course folder.
Share 1
With a partner or group, compare your answers from questions 3 and 5 of Try This 1. Explain any differences.
If required, save a record of your discussion in your course folder.
1 Adapted from Pre-Calculus 12. Whitby, ON: McGraw-Hill Ryerson, 2011. Reproduced with permission.
1.2. Explore
Module 6: Exponents and Logarithms
Explore
In Try This 1 you were solving logarithmic equations. A logarithmic equation is an equation in which there is a logarithm of a variable. You may have found that when a logarithmic equation is in the form logc L = logc R, where the left side and right side each contain a single logarithm with the same base, the logarithms can be removed.
- If logc L = logc R, where c, L, R > 0 and c ≠ 1, then L = R.
Read “Link the Ideas” on page 406 of the textbook. Notice that a proof of the preceding property is provided.
In Try This 2 you will use this property: if logc L = logc R, then L = R. You will explore how to solve a more difficult logarithmic equation.
Try This 2
Use the logarithmic equation log2 (x − 2) + log2 (x + 1) = 2 for the following questions.
- Using a law of logarithms, write the left side of the equation as a single logarithm.
- Use your answer from question 1 and write the equation with the single logarithm on the left side and “equal to 2” on the right side. Change the equation to exponential form and solve for x.
- Write the right side of the equation as a single logarithm. This logarithm should have the same base as the logarithm on the left side and the logarithm should equal 2.
- Use your answers from questions 1 and 3 to solve the equation for x.
- How could you check to see if your answers are correct?
- Are all of your solutions correct? Explain your answer.
- Explain why the logarithm of a negative number is undefined.
Save your responses in your course folder.
1.3. Explore 2
Module 6: Exponents and Logarithms
In Try This 2 you may have used the product law to write the left side of the equation as a single logarithm.
log2 (x − 2)(x + 1) = 2
There is more than one method you could use to solve this equation.
Method 1: Change to Exponential Form |
Method 2: Change the Right Side |
|
Since 2 = log2 22 or 2 = log2 4, 2 = log2 4 replaces the right side.
|
The same solutions are found using Method 1 or Method 2. Are these solutions correct?
Determine the restriction from the original equation, log2 (x − 2) + log2 (x + 1) = 2. Remember from Lesson 5 that the logarithm of a negative number is undefined.
Always check to see if the solutions are defined for the equation.
The solutions found algebraically are x = −2 and x = 3. The solution x = −2 must be extraneous since it is a restricted value. Therefore, x = 3 is the solution.
You can also verify your solutions by substituting each into the original equation and checking whether the left side of the equation equals the right side of the equation.
Substitute x = −2.
| LS | RS |
|
2 |
Left Side ≠ Right Side
Since the logarithm of a negative number is undefined, the solution x = −2 is extraneous.
Substitute x = 3.
| LS | RS |
|
2 |
Left Side = Right Side
So, the solution is x = 3.
Read “Example 1” on pages 406 to 408 of the textbook. Notice the following while reading:
- Part a, Method 2 shows a graphical solution. This is a way to solve, but the focus of this lesson is on using algebraic methods to solve equations.
- Part b shows two methods. One method changes both sides of the equation to logarithms, and the second method changes the equation to exponential form. Which method do you prefer?
Self-Check 1
- Complete “Your Turn” at the end of “Example 1” on page 408 of the textbook. Answer
- Complete questions 4.a., 4.c., and 6 on page 413 of the textbook. Answer
- Complete question 12 on page 414 of the textbook. Answer
- Complete the numerical response question Solving Logarithmic Equations.
In Lesson 2 you examined how to solve exponential equations. In some cases the bases were powers of one another, and in other cases the bases were not powers of one another. When the bases were not powers of one another, you estimated different values and then checked to see which solution was correct.
Do you think there is a more efficient way to solve exponential equations in which the bases are not powers of one another?
In Try This 3 you will investigate two different methods that can be used to solve exponential equations.
Try This 3
Complete questions 4 to 8 from “Part B: Explore Exponential Equations” on pages 405 to 406 of the textbook.
Save your responses in your course folder.
Share 2
With a partner or group, share your responses to Try This 3, and then discuss the following question:
Which method could be considered the more “universal” method or the method that would work most consistently for any exponential equation? Discuss advantages and disadvantages for this method.
If required, save a record of your discussion in your course folder.
1.4. Explore 3
Module 6: Exponents and Logarithms
In Try This 3 you may have noticed that logarithms can be used to solve exponential equations. Logarithms are especially helpful where the exponential equations contain bases that are not powers of one another and a common base cannot be found.
Remember these important points when solving exponential equations:
- Take the logarithm of each side of the equation and then use the property if A = B, then logc A = logc B, where c, A, B > 0 and c ≠ 1.
- The base of the logarithm used is often base 10, but any base can be used as long as the bases on each side of the equation are the same.
- Once the logarithm has been applied, the laws of logarithms can be used to simplify the equation and solve for the variable.
There are two methods that can be used for some equations. One method is to take the logarithm of each side of the equation. The other method that may be used is to convert the exponential equation to logarithmic form. This second method works when there is a variable as an exponent on only one side of the equation.
Read “Example 2” on pages 408 to 409 of the textbook. Notice the following points when reading:
- There are two methods that could be used in part a of the example. Only one method is shown for parts b and c.
- Each value was checked to verify that the solution is correct.
- The answers were rounded to two decimal places. The answer above the approximate solution is considered the exact value of the solution.
Self-Check 2
- Complete “Your Turn” at the end of “Example 2” on page 409 of the textbook. Answer
- Complete the matching activity Solving Exponential Equations Using Logarithms.
1.5. Explore 4
Module 6: Exponents and Logarithms
In Try This 4 you will explore how exponential equations can be used to solve problems involving investments and credit cards.
Try This 4
Hemera/Thinkstock
Answer the following questions using the compound interest formula A = P(1 + i)n, where
- A is the future value
- P is the present value
- i is the interest rate per compounding period, as a decimal
- n is the number of compounding periods
Scenario 1
Eoghan (pronounced Ewan) receives a gift of $500 and decides to invest in a GIC (guaranteed investment certificate) that earns 5.5% per year, compounded semi-annually. Determine how long it will take for Eoghan’s GIC to be worth $700 by answering the following questions.
- Determine the following variables, and identify the unknown variable.
- A
- P
- i
- n
- Substitute the values from question 1 into the formula A = P(1 + i)n. Solve for the unknown variable.
- Use your answer from question 2 to determine how many years it will take for the GIC to be worth $700.
iStockphoto/Thinkstock
Scenario 2
Jia used a credit card to purchase an $850 tablet computer. The interest rate charged on overdue balances is 18% per year, compounded daily. Answer the following questions to determine how many days Jia’s payment is overdue if the amount owed on her credit card is $875.
- Use the compound interest formula to determine the following variables. Make sure to identify the unknown variable.
- A
- P
- i
- n
-
Substitute the values from question 4 into the formula A = P(1 + i)n. Solve for the number of days the balance is overdue.
- Compare the procedures you used to solve questions 2 and 5. What stayed the same and what changed in the two procedures?
Save your responses in your course folder.
Comstock/Thinkstock
The Diners Club, introduced in 1950, was the first universal credit card. Today, many adults have at least one credit card. In fact, to rent a car, you must have a credit card. There is an element of risk to a financial institution in extending credit to individuals. Many credit cards charge a high interest rate on balances not paid after a month. These interest rates are usually compounded daily.
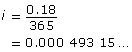
1.6. Explore 5
Module 6: Exponents and Logarithms
In Try This 4 you may have noticed that the compound interest formula can be used to determine how long it would take for an amount of money to increase thanks to compound interest. In Scenario 1 you may have determined that it would take about 6.5 yr for the amount of money Eoghan invested to increase to $700.
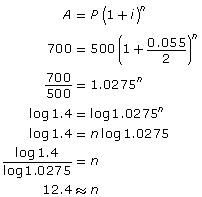
The number of compounding periods is approximately 12.4. The interest is compounded semi-annually, which means there would be 2 compounding periods each year. So, the number of years would be 12.4 ÷ 2 = 6.2, or approximately 6.2 yr. To be sure the value is at least $700, the money would have to remain invested for 6.5 yr, when interest is compounded again.
The question involving the credit card would use a similar procedure, except that the credit card interest is compounded daily. The different compounding period would change how i is calculated, and n would be in days. In Scenario 2 you should have found that Jia’s payment was about 59 d overdue.
Many real-world applications can be modelled using an exponential equation. The form 
where b > 0, can be used to model a situation. Open 
where b > 0, and roll over each variable to explore the equation. Note that t often represents time as in this demonstration; however, it is also possible to use this form of equation when t represents something other than time.
1.7. Explore 6
Module 6: Exponents and Logarithms
Read “Example 4” on page 411 of the textbook. Notice the following points when reading:
- There is no formula given in the question. The formula was determined using the form
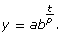
- The original amount of C-14 was not required to solve this problem.
- This problem could also have been solved using the method of converting from exponential to logarithmic form.
- p and t are in the same units—years.
- b < 0 because the question is about decay.
Self-Check 3
- Complete “Your Turn” at the end of “Example 4” on page 411 of the textbook. Answer
- Complete questions 14, 16, and 17 on pages 414 and 415 of the textbook. Answer
At some point in your life you will likely want to buy a home. Most people need a loan to purchase a home. This loan is called a mortgage. In order to qualify for a mortgage in Canada, you need to have a down payment of 5%, and you need to prove that you can pay your bills.
The financial institution that issues the mortgage will determine how much money you can borrow based on your ability to repay the mortgage. If you cannot repay the mortgage, the financial institution can seize your other assets, including money in savings accounts, cars you own, and so on.
Add logarithmic equation to your copy of Glossary Terms.
Add the following formulas to your copy of Formula Sheet.
- A = P(1 + i)n
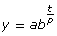
1.8. Connect
Module 6: Exponents and Logarithms
Complete the Lesson 6 Assignment that you saved in your course folder at the beginning of the lesson. Show work to support your answers.
Save your responses in your course folder.
Project Connection
You are ready to apply your understanding of the relationship between a function and the square root of the function. Go to Module 6 Project: Movie Money. Complete Part 3 and Conclusion.
Save your responses in your course folder.
You will submit your work from the Module 6 Project to your teacher once you have completed the project.
1.9. Lesson 6 Summary
Module 6: Exponents and Logarithms
Lesson 6 Summary
In this lesson you explored how to solve logarithmic and exponential equations.
To solve a logarithmic equation, apply the laws of logarithms to express the left side and the right side of the equation as a single logarithm. You can then use the property if logc A = logc B, then A = B, where c, A, B > 0 and c ≠ 1.
To solve an exponential equation where the bases are not powers of one another, you can use the property if A = B, then logc A = logc B, where c, A, B > 0 and c ≠ 1.
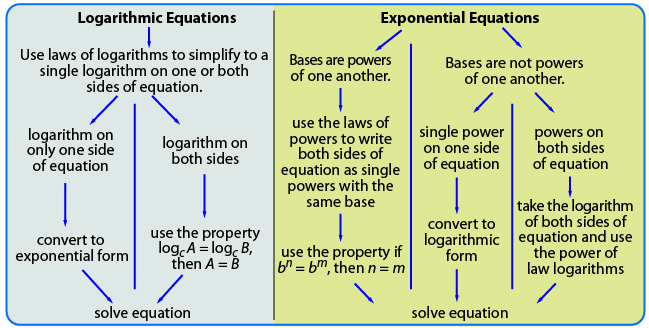
Check that solutions satisfy the original equation. Remember that the logarithm of a number ≤ 0 is undefined.
There are real-world situations that can be modelled with an exponential or logarithmic equation. Some applications involve finances, such as investments and loans. Other applications can be found in science, such as radioactive decay. Many exponential equations can be expressed in the form 