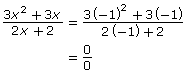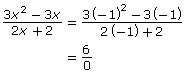Lesson 2
| Site: | MoodleHUB.ca 🍁 |
| Course: | Math 30-1 SS |
| Book: | Lesson 2 |
| Printed by: | Guest user |
| Date: | Saturday, 27 December 2025, 3:31 AM |
Description
Created by IMSreader
1. Lesson 2
Module 7: Rational Functions and Function Operations
Lesson 2: Analyzing Rational Functions
Focus

© Sandra van der Steen/
14821564/Fotolia
When preparing goods for transport, the cost of packaging is one factor to consider. Typically, packaging in bulk is cheaper. Can you think of some reasons for this?
One measure of efficiency of packaging is the volume-to-surface-area ratio of the container. This ratio increases as the size of the container increases. This means that if you double the volume, you will require less than double the amount of packaging if the package shape remains the same. This is one reason packaging in bulk is cheaper. While modelling the volume-to-surface-area ratio, you will see that more than one type of “break” is possible in the graph of a function.
In this lesson you will explore how some rational functions can have discontinuities that are not asymptotes.
Lesson Outcomes
At the end of this lesson you will be able to
- describe what a discontinuity is
- explain the difference between an asymptote and a point of discontinuity and determine when each will occur
Lesson Question
You will investigate the following question:
- How can you determine when a discontinuity will occur in a function and what kind of discontinuity it will be?
Assessment
Your assessment may be based on a combination of the following tasks:
- completion of the Lesson 2 Assignment (Download the Lesson 2 Assignment and save it in your course folder now.)
- course folder submissions from Try This and Share activities
- additions to Glossary Terms
1.1. Discover
Module 7: Rational Functions and Function Operations
Discover

iStockphoto/Thinkstock
Try This 1
Suppose you are working with a vegetable cannery to design aluminum can dimensions. You have been asked to work specifically with the volume-to-surface-area ratio. The company has asked that all cans have a height of 11.5 cm so that the cans will fit on shelves properly.
-
- Give a function, V(r), that gives the volume as a function of the radius of the can.

- Give a function, S(r), that gives the surface area as a function of the radius.

- The volume-to-surface-area ratio as a function of height can be written as
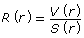 . Expand this expression using the functions from question parts a. and b.
. Expand this expression using the functions from question parts a. and b. 
- Simplify the function R(r) by cancelling common factors, and determine any non-permissible values for R(r).

- Give a function, V(r), that gives the volume as a function of the radius of the can.
-
- Describe what happens to the volume-to-surface-area ratio as r increases and the height is kept at 11.5 cm.

- Explain how much the volume-to-surface-area ratio should influence the can dimensions selected.
- Describe what happens to the volume-to-surface-area ratio as r increases and the height is kept at 11.5 cm.
-
- r = 0 and r = −11.5 are non-permissible values for R(r). Ignoring physical limitations, explain where each of these values comes from.
- Complete a table like the following for the values near the two non-permissible values:
r R(r) r R(r) −0.1 −11.6 −0.01 −11.51 −0.001 −11.501 0 indeterminate −11.5 undefined 0.001 −11.499 0.01 −11.49 0.1 −11.4 - Explain what happens to the value of R(r) as r approaches each non-permissible value.
- Calculate the value of the numerator and denominator when R(r) is indeterminate and when R(r) is undefined. Use this information to predict the difference between an indeterminate and an undefined value.
-
- Graph
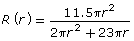 and
and 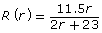 using technology.
using technology. - Can you tell where the undefined value at r = −11.5 occurs just by looking at either graph?
- Can you tell where the indeterminate value at r = 0 occurs just by looking at either graph?
- What value does
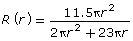 give for r = 0? What restriction should be placed on
give for r = 0? What restriction should be placed on 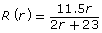 ?
?
- Graph
![]() Save your responses in your course folder.
Save your responses in your course folder.
πr is a factor common to the numerator and denominator:
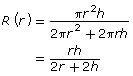
1.2. Explore
Module 7: Rational Functions and Function Operations
Explore
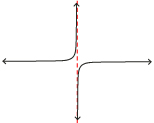
In Try This 1 you saw that the rational function ![]() contained two non-permissible values at r = 0 and r = −11.5. Both of these values created a discontinuity in the graph of the function; that is, you couldn’t draw the graph without lifting your pencil. One of these discontinuities showed up as an asymptote. You have seen these many times before. The other discontinuity showed up as a “missing” point on the function. This missing point is called a point of discontinuity or a hole and is usually represented with an open circle on the graph.
contained two non-permissible values at r = 0 and r = −11.5. Both of these values created a discontinuity in the graph of the function; that is, you couldn’t draw the graph without lifting your pencil. One of these discontinuities showed up as an asymptote. You have seen these many times before. The other discontinuity showed up as a “missing” point on the function. This missing point is called a point of discontinuity or a hole and is usually represented with an open circle on the graph.
If the function ![]() is simplified to
is simplified to ![]() , the restriction r ≠ 0 needs to be placed on the function to maintain the original restrictions.
, the restriction r ≠ 0 needs to be placed on the function to maintain the original restrictions.
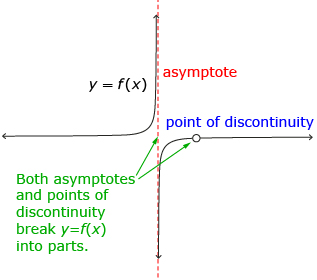

The graph of this rational function does not appear to have any
points of discontinuity; however, by checking the table of values,
you can see that −2 is a point of discontinuity.
Although some graphing software will show where points of discontinuity occur when a rational function is graphed, many graphing calculators do not. It is up to the user to determine where these points occur and to interpret the graph correctly.
If a graphing calculator shows a table of values for a function, this can sometimes be used to determine where a point of discontinuity is. Typically the y-value corresponding to the non-permissible x-value will show some type of error message.
1.3. Explore 2
Module 7: Rational Functions and Function Operations
In Try This 2 you will further explore when asymptotes occur and when points of discontinuity occur.
Try This 2
Consider the following two rational functions:
-
- Determine the non-permissible value for f(x) and g(x).
- Graph f(x) and g(x) using technology and make a sketch of the graphs.
- Use your graphs to complete a table like the following.
f(x) g(x) Non-permissible Value Description of Graph at Non-permissible Value Description of Graph Near Non-permissible Value
- Try to explain why a point of discontinuity occurs in f(x) and an asymptote occurs in g(x).
-
- Factor the numerator and denominator for both functions using common factors.
- Cancel any factors that appear in both the numerator and denominator.
- Revise your explanation for question 2, if necessary.
![]() Save your responses in your course folder.
Save your responses in your course folder.
Share 1
With a partner or group, compare, share, and discuss your responses to Try This 2. Based on your discussion, develop a general statement describing how to determine if a non-permissible value is indeterminate or undefined. How does this relate to factors in the numerator and denominator?1
![]() If required, save a record of your discussion in your course folder.
If required, save a record of your discussion in your course folder.
1 Source: Pre-Calculus 12. Whitby, ON: McGraw-Hill Ryerson, 2011. Reproduced with permission.
1.4. Explore 3
Module 7: Rational Functions and Function Operations
The main difference between the two functions in Try This 2 is that the non-permissible value for one produced a point of discontinuity and the other produced an asymptote.
| When a factor that occurs in both the numerator and denominator is equal to 0 | When a factor that occurs only in the denominator is equal to 0 | |
| Function | ||
| Non-permissible Values | x = −1
|
x ≠ −1
|
| Type of Non-permissible Value | indeterminate | undefined |
| Appearance on Graph | hole or point of discontinuity
|
asymptote
|
| Factored Form | 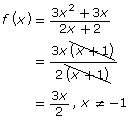 |
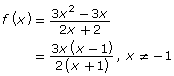 |
Common Factors
|
Yes, a factor in the numerator and in the denominator causes a hole. | No, a factor only in the denominator causes an asymptote. |

A formal definition of division is ![]() if and only if a = bc. A division by 0 fails this definition. If you begin with
if and only if a = bc. A division by 0 fails this definition. If you begin with ![]() , then a = 0c also needs to be true—it is not for any a ≠ 0. This is why a division by 0 is usually said to be undefined.
, then a = 0c also needs to be true—it is not for any a ≠ 0. This is why a division by 0 is usually said to be undefined.
An exception occurs when a = 0. This gives ![]() , or 0 = 0c, which is true for any c. By this definition,
, or 0 = 0c, which is true for any c. By this definition, ![]() is equal to any value.
is equal to any value. ![]() is often referred to as indeterminate.
is often referred to as indeterminate.
You do not need to understand indeterminate values for this course. You only need to recognize that indeterminate values will cause points of discontinuity to appear on the graph of a rational function.
1.5. Explore 4
Module 7: Rational Functions and Function Operations
Self-Check 1
![]()
- Complete “Your Turn” from “Example 2” on page 449 of the textbook. Answer
- Complete questions 1, 2.a., 2.b., and 3 on page 451 of the textbook. Answer
So far, you have looked at what happens if a factor occurs in both the numerator and denominator and if a factor occurs just in the denominator of a rational function. In Try This 3 you will look at what happens when a factor is only in the numerator.
Try This 3
Consider the rational function ![]() .
.
-
- What factor occurs only in the numerator?
- What factor occurs only in the denominator?
- What factor occurs in both the numerator and denominator?
- Using the information from question 1, predict where a point of discontinuity and an asymptote will occur on the graph of y = f(x).
-
- Graph y = f(x) to check your predictions from question 2.
- What occurs on the graph when the factor that is only in the numerator is equal to 0?

-
- Predict whether the event you found in question 3.b. always occurs when a factor is in the numerator but not the denominator.
- Explain how you can further test this prediction.
- Use your strategy to test your prediction.
- Use “General Form of a Rational Function” to check your predictions from question 4.

- Use “General Form of a Rational Function” from question 5 to graph the following functions. State the x-intercepts for each function.
- How does the prediction you made in question 4 relate to the intercepts you found in question 6?
![]() Save your responses in your course folder.
Save your responses in your course folder.
Share 2
With a partner or group, discuss the following question based on the information from Try This 3:
How can you explain the phenomenon of determining the x-intercept using ideas from earlier in this course or previous courses?
![]() If required, save a record of your discussion in your course folder.
If required, save a record of your discussion in your course folder.
1.6. Explore 5
Module 7: Rational Functions and Function Operations
In Try This 3 you may have noticed that an x-intercept occurs when a factor that only occurs in the numerator is equal to 0. This is because this makes the entire numerator 0, and, therefore, the function 0.
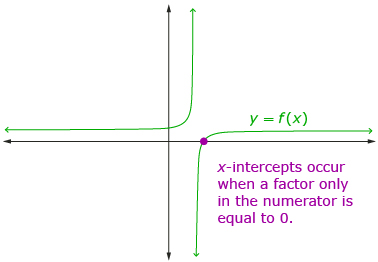
Read “Example 3” on pages 449 and 450 of the textbook. Pay attention to how asymptotes, points of discontinuity, and x-intercepts are used to help match the equations to their graphs.
Self-Check 2
- Add another column to the summary table you saw just after Try This 2. The first row of your table will look like this:
When a factor that occurs in both the numerator and denominator is equal to 0 When a factor that occurs only in the denominator is equal to 0 When a factor that occurs only in the numerator is equal to 0 Function 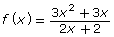
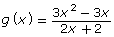
Functions will vary. An example is provided.
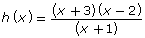
Complete the last column to describe what happens if there is a factor that occurs only in the numerator. Answer
![]()
- Complete “Your Turn” from “Example 3” on page 450 of the textbook. Answer
- Complete questions 4, 5, 8.a., 8.b., and 11 on pages 452 and 453 of the textbook. Answer
- discontinuity
- point of discontinuity
- hole
1.7. Connect
Module 7: Rational Functions and Function Operations
Complete Lesson 2 Assignment that you saved in your course folder at the beginning of this lesson. Show work to support your answers.
![]() Save your responses in your course folder.
Save your responses in your course folder.
Project Connection
There is no Project Connection in this lesson.
1.8. Lesson 2 Summary
Module 7: Rational Functions and Function Operations

Lesson 2 Summary
In this lesson you explored what happens on the graph of a rational function when it has a factor equal to 0 that occurs only in the numerator, only in the denominator, and in both the numerator and the denominator. If the 0 is only in the numerator, an x-intercept occurs. If the 0 is only in the denominator, an asymptote occurs. If the 0 shows up in both the numerator and denominator, a point of discontinuity occurs.
In the next lesson you will explore how the characteristics of a rational function can be used to sketch the function’s graph.