Lesson 4
| Site: | MoodleHUB.ca 🍁 |
| Course: | Math 30-1 SS |
| Book: | Lesson 4 |
| Printed by: | Guest user |
| Date: | Saturday, 27 December 2025, 3:36 AM |
Description
Created by IMSreader
1. Lesson 4
Module 7: Rational Functions and Function Operations
Lesson 4: Adding and Subtracting Functions
Focus

Hemera/Thinkstock
Pumping gas, travelling a toll road, buying a car, using an airport: tax is everywhere and must be calculated into the cost of transportation. The Goods and Services Tax, or GST, is a visible tax in Canada. When you purchase most goods or services in Canada, you have to pay for the item or service as well as the GST. Do you calculate the tax on something you buy in one or two steps? Is it possible to give a rule that explains how any percentage tax can be calculated? Can you think of a rule that shows the change in the amount paid if the tax rate changes?
In this lesson you will explore how multiple functions can be combined using addition or subtraction.
Lesson Outcomes
At the end of this lesson you will be able to
- add and subtract functions
- determine the domain and range of the sum or difference of functions
Lesson Question
You will investigate the following question:
- How can functions be added or subtracted?
Assessment
Your assessment may be based on a combination of the following tasks:
- completion of the Lesson 4 Assignment (Download the Lesson 4 Assignment and save it in your course folder now.)
- course folder submissions from Try This and Share activities
- additions to Formula Sheet
1.1. Launch
Module 7: Rational Functions and Function Operations
Launch
Do you have the background knowledge and skills you need to complete this lesson successfully? Launch will help you find out.
Before beginning this lesson you should be able to
- write function notation
- determine points of a function
- represent a function as an equation, graph, or table of values
1.2. Are You Ready?
Module 7: Rational Functions and Function Operations
Are You Ready?
Complete these questions. If you experience difficulty and need help, visit Refresher or contact your teacher.
- Write y = 3x2 − 4x + 5 in function notation. Answer
- A football leaves a field goal kicker’s foot at 64 ft/s. The distance, D(t), in feet, that the football is above the field at any time, t, in seconds, is given by the function D(t) = −16t2 + 64t.
- Create a table of values, being careful to pick appropriate values of t. (It does not make sense to use negative values for time in this context.) Answer
- From the table of values, create a graph of the function. Answer
- What is the maximum height that the football reaches? At what time does that occur? How did you figure that out? Answer
- How would you express the point (4, 0) in function notation, and what do the values of the point indicate in the context of the problem? Answer
If you answered the Are You Ready? questions without difficulty, move to Discover.
If you found the Are You Ready? questions difficult, complete Refresher.
1.3. Refresher
Module 7: Rational Functions and Function Operations
Refresher
Watch “Introduction to Functions.”
Go back to the Are You Ready? section and try the questions again. If you are still having difficulty, contact your teacher.
1.4. Discover
Module 7: Rational Functions and Function Operations
Discover
Try This 1
In 2008, the GST rate in Canada was reduced from 7% to 5%.
| Cost of Item ($) | Amount Paid Before Tax ($) | 5% GST ($) | 7% GST ($) | Total Cost with 5% GST ($) | Total Cost with 7% GST ($) | Difference in Tax Amount ($) |
| 1 | 1 | 0.05 | 0.07 | 1.05 | 1.07 | 0.02 |
| 2 | 2 | 0.10 | 0.14 | 2.10 | 2.14 | 0.04 |
| 3 | 3 | 0.15 | 0.21 | 3.15 | 3.21 | 0.06 |
| 4 | 4 | 0.20 | 0.28 | 4.20 | 4.28 | 0.08 |
| 5 | 5 | 0.25 | 0.35 | 5.25 | 5.35 | 0.10 |
- Explain how the values in each of the columns can be determined.
-
- Explain a two-step process that can be used to determine the Total Cost with 5% GST from the cost of the item.
- Explain a one-step process to determine the Total Cost with 5% GST from the cost of the item.
- Explain a one-step process that can be used to determine the Difference in Tax Amount.
- Why might you be interested in using a one-step process instead of a multi-step process for these calculations?
- Open Calculating Tax.
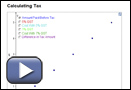
- Select to show only the plots for Amount Paid Before Tax, 5% GST, and Cost with 5% GST.
- Explain how the Cost with 5% GST points can be determined from the Amount Paid Before Tax points and the 5% GST points.
- Select to show only the 5% GST, 7% GST, and Difference in Tax Amount points. Explain how the Difference in Tax Amount points can be determined from the 5% GST points and the 7% GST points.
![]() Save your responses in your course folder.
Save your responses in your course folder.
Share 1
With a partner or group, discuss the following question based on the information from Try This 1:
Suppose f(x) and g(x) represent the amount of tax paid on x dollars of goods purchased. How could you represent the difference in the amount paid for these two tax rates?
![]() If required, save a record of your discussion in your course folder.
If required, save a record of your discussion in your course folder.
1.5. Explore
Module 7: Rational Functions and Function Operations
Explore
In Try This 1 you explored how some values related to GST can be determined. For some of the values, you added or subtracted previously calculated values.
For example, to determine the difference in the amount of tax, you may have
-
determined the amount of tax at 7% (0.07x)

iStockphoto/Thinkstock
- determined the amount of tax at 5% (0.05x)
- subtracted the two amounts (0.07x − 0.05x = 0.02x)
It is possible to use function notation to describe this process. Let
- x be the amount purchased
- f(x) be the amount of tax paid at 7%
- g(x) be the amount of tax paid at 5%
- h(x) represent the difference between the two amounts
You can then write h(x) = f(x) − g(x), which is sometimes written as h(x) = (f − g)(x). In this scenario,
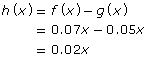
The advantage to writing the difference of the two functions as one function in function notation is that it allows you to make more general statements. For example, you can define p(x) and q(x) as the amounts of tax paid on a purchase of x dollars, and then define r(x) as the difference. This means you can write r(x) = p(x) − q(x) without even knowing how p(x) and q(x) can be determined!
Just as you could subtract two functions, it is also possible to add two functions. You could write the sum of the two functions as h(x) = f(x) + g(x), which can also be written h(x) = (f + g)(x).
In Try This 2 you will explore how specific functions can be added.
Try This 2
Consider the functions f(x) = x2 + x and g(x) = 3x − 1.
- Use the functions noted to complete the following table.
x f(x) g(x) 

−5 −2 0 2 5 -
- Substitute f(x) = x2 + x and g(x) = 3x − 1 into h(x) = f(x) + g(x).
- Use the resulting expression to determine h(x) when x = −5, −2, 0, 2, and 5.
- Substitute f(x) = x2 + x and g(x) = 3x − 1 into p(x) = f(x) − g(x).
- Use the resulting expression to determine p(x) when x = −5, −2, 0, 2, and 5.
- How did the values you determined in questions b. and d. relate to the values you determined in the table in question 1?
- Suggest a general rule for adding or subtracting functions that are written as equations.
![]() Save your responses in your course folder.
Save your responses in your course folder.
1.6. Explore 2
Module 7: Rational Functions and Function Operations
Although any symbol can be used to represent a function or variable, some letters are more likely to be used than others. It is common in mathematics to pick particular letters for different jobs. This can make reading the math a bit easier because it can give you a clue to what the letter represents. Here are some common uses of lowercase Latin letters.
| a, b, c, d | parameters (unspecified constants) |
| e | Euler’s number (2.718…) |
| f, g, h | functions |
| i | the imaginary unit (i2 = −1), integer variable |
| j, k | integer variables |
| l | avoided because it looks like a 1 |
| m, n | integer variables |
| o | avoided because it looks like a 0 |
| p | unspecified prime number, polynomial function |
| q | unspecified quotient, polynomial function |
| r | unspecified remainder, variable that is a radius |
| s | variable that is an arc length or speed |
| t | variable that is a time |
| u, v, w, x, y, z | variables that are real numbers |
In addition, many capital letters, Greek letters, and other symbols have typical uses. The context will also give clues to how different symbols are used.
In Try This 2 you may have found that adding and subtracting functions is quite simple. You just add or subtract them!
In Try This 2 you saw that if f(x) = x2 + x and g(x) = 3x − 1, then
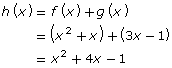 |
and | 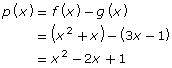 |
For some additional examples of how functions can be added or subtracted, read “Example 1” on pages 476 and 477 of the textbook or “Example 2” on pages 478 and 479.
Self-Check 1
Complete questions 1.a., 1.d., 2.a., 2.d., 3.a., 3.c., 9.b., 9.c., 10.a., and 11.d. on pages 483 and 484 of the textbook. Answer
1.7. Explore 3
Module 7: Rational Functions and Function Operations
It is possible to predict what the graph of a function that was produced by adding or subtracting two other functions will look like. Try This 3 explores this idea.
Try This 3
Consider the following two functions:
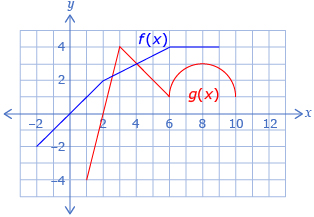
- Predict what graphs of the functions h(x) = (f + g)(x) and p(x) = (f − g)(x) will look like.
- Use the graphs of f(x) and g(x) to complete a table like the following.

x f(x) g(x) h(x) = (f + g)(x) p(x) = (f − g)(x) q(x) = (g − f)(x) −2 −2 undefined −1 −1 undefined 0 0 undefined 1 1 −4 
2 2 0 3 2.5 4 4 3 3 5 3.5 2 6 4 1 7 4 2.7 8 4 3 9 4 2.7 10 undefined 1 - Either print the Printable Template or make a sketch of the information. Then use this data to sketch h(x), p(x), and g(x).
-
- Describe a strategy you could use to graph h(x) given the graphs of f(x) and g(x).
- Describe a strategy you could use to graph p(x) given the graphs of f(x) and g(x).
-
- Describe how the domain and range of f(x) and g(x) are related to the domain and range of h(x), p(x), and q(x).
- Describe the relationship between the graph of p(x) and the graph of q(x).
![]() Save your responses in your course folder.
Save your responses in your course folder.
Share 3
With a partner or group, discuss the following question based on your graphs created in Try This 3:
Describe a rule to determine the domain of r(x) using s(x) and t(x) if r(x) = s(x) + t(x).
![]() If required, save a record of your discussion in your course folder.
If required, save a record of your discussion in your course folder.
1.8. Explore 4
Module 7: Rational Functions and Function Operations
In Try This 3 you may have noticed that it is possible to add or subtract functions using only their graphs. Watch Adding Functions to see two added functions. Compare this strategy to your strategy.
Subtracting functions follows a nearly identical process, except that the y-values are subtracted instead of being added.
Read “Example 3” on pages 480 to 481 of the textbook to see an example of how functions can be added by using their graphs. Compare the method of adding the y-coordinates of corresponding points to the methods you have seen so far.
To see how the sum of two functions is affected by manipulating the individual functions, try Adding and Subtracting Functions, which gives the function (f + g)(x) = f(x) + g(x) and allows you to manipulate f(x) and g(x) to see how (f + g)(x) changes. Try both the addition and subtraction functions.
Self-Check 2
1.9. Explore 5
Module 7: Rational Functions and Function Operations
The addition or subtraction of functions can be used to solve problems that include adding or subtracting values defined by functions. Try This 4 explores a financial example involving adding and subtracting functions.
Try This 4

iStockphoto/Thinkstock
Suppose that you make two investments, each of $1000. The first investment is in a savings account so that you can access the money if necessary. The second one is in a savings bond that you do not plan to redeem until the bond has matured. The savings account pays an interest rate of 3% per annum, and the bond pays an annual rate of 5%. Assume that the interest is compounded annually and that the value of either investment can be determined for any time, t. Both investments will be removed after 8 yr. ![]()
-
- Give the equation of a function S(t) that represents the value of the savings investment after t years.

- Give the equation of a function B(t) that represents the value of the bond investment after t years.
- Give the equation of a function S(t) that represents the value of the savings investment after t years.
-
- Give the equation of a function T(t) that represents the total value of the investments after t years.
- Give the equation of a function D(t) that represents how much more money is invested in bonds than in the bank account after t years.
-
- Determine T(6) and D(6). Explain what each value represents.
- Determine a time when one investment is worth $100 more than the other.

- Determine a time when the investments are worth $2500 together.

- Determine the domain and range of each of the four functions.
![]() Save your responses in your course folder.
Save your responses in your course folder.
1.10. Explore 6
Module 7: Rational Functions and Function Operations
In Try This 4 you may have noticed that it is sometimes easier to use the addition or subtraction of functions to solve a problem. For example, to determine the time when one investment is worth $100 more than another, you could use
![]()
Then you can estimate a solution to 100 = 1000(1.05)t − 1000(1.03)t. Without this function, you would have likely needed to guess and check using B(t) and S(t).
For an example of an application of subtracting functions, read “Example 4” on pages 481 and 482 of the textbook.
Self-Check 3
- Complete “Your Turn” from “Example 4” on page 482 of the textbook. Answer
- Complete question 14 on page 485 of the textbook. Answer
- (f + g)(x) = f(x) + g(x)
- (f − g)(x) = f(x) − g(x)
1.11. Connect
Module 7: Rational Functions and Function Operations
Complete the Lesson 4 Assignment that you saved in your course folder at the beginning of this lesson. Show work to support your answers.
![]() Save your responses in your course folder.
Save your responses in your course folder.
Project Connection
There is no Project Connection in this lesson.
1.12. Lesson 4 Summary
Module 7: Rational Functions and Function Operations
Lesson 4 Summary
In this lesson you saw that it is possible to add and subtract functions. The notation h(x) = f(x) + g(x) is equivalent to h(x) = (f + g)(x), and h(x) = f(x) − g(x) is equivalent to h(x) = (f − g)(x). To add functions using their graphs, add the y-coordinates for any x-coordinate. Similarly, to subtract functions using their graphs, subtract the y-coordinates for any x-coordinate.
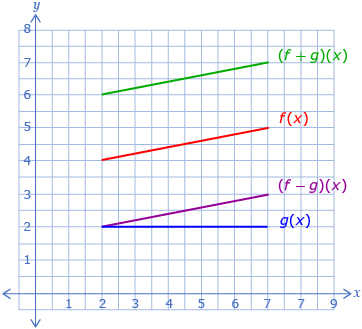
In Lesson 5 you will learn how to multiply and divide functions.