Lesson 1
| Site: | MoodleHUB.ca 🍁 |
| Course: | Math 30-1 SS |
| Book: | Lesson 1 |
| Printed by: | Guest user |
| Date: | Tuesday, 9 December 2025, 11:28 PM |
Description
Created by IMSreader
1. Lesson 1
Module 8: Permutations, Combinations, and the Binomial Theorem
Lesson 1: Fundamental Counting Principle
Focus

Comstock/Thinkstock
One of the ways people are identified is by phone numbers. In the not-too-distant past, one phone number was often associated with an entire family. Now, however, many people possess individual cellphones and their own unique phone numbers.
Prior to 1999, the area code for the entire province of Alberta was 403. In 1999, the southern half of the province retained the 403 area code, and the northern half was assigned the new area code of 780. In September 2008, Alberta added another area code, 587, across the province as available phone numbers were again running out. By adding another area code there is a potential for nine million more phone numbers.
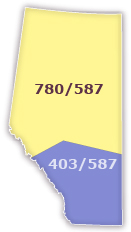
Adapted from base map
© Map Resources
Can you think why people in Alberta continue to need more phone numbers? By the end of this lesson you will be able to show that a new area code does indeed amount to nine million new phone numbers.
Determining the number of ways things may occur is a branch of mathematics called combinatorics. This branch is used in many ways: from designing a computer network to coding your garage door opener to determining the chances of winning the lottery.
Lesson Outcomes
At the end of this lesson you will be able to
- use the fundamental counting principle to solve problems
- use a new notation, called factorial notation, to determine the number of arrangements of items
Lesson Questions
You will investigate the following questions:
- How can you use the fundamental counting principle to determine the number of outcomes in a given problem?
- What is factorial notation and when is it used to solve problems?
Assessment
Your assessment may be based on a combination of the following tasks.
- completion of the Lesson 1 Assignment (Download the Lesson 1 Assignment and save it in your course folder now.)
- course folder submissions from Try This and Share activities
- additions to Glossary Terms and Formula Sheet
- work under Project Connection
Self-Check activities are for your own use. You can compare your answers to suggested answers to see if you are on track. If you are having difficulty with concepts or calculations, contact your teacher.
Remember that the questions and activities you will encounter provide you with the practice and feedback you need to successfully complete this course. You should complete all questions and place your responses in your course folder. Your teacher may wish to view your work to check on your progress and to see if you need help.
Time
Each lesson in Mathematics 30-1 LearnEveryware is designed to be completed in approximately two hours. You may find that you require more or less time to complete individual lessons. It is important that you progress at your own pace, based on your individual learning requirements.
This time estimation does not include time required to complete Going Beyond activities or the Module Project.
1.1. Discover
Module 8: Permutations, Combinations, and the Binomial Theorem
Discover

iStockphoto/Thinkstock
If your Personal Identification Number (PIN) consists of four digits, how long do you think it would take a thief to hack your number? In theory there are 10 000 possible PINs available but, in reality, most banks have restrictions on what digits may be used. Most bank machines only allow three attempts to get the correct PIN, so there is only a 0.06% chance of a thief getting the correct number before the machine locks the crook out.
Try This 1
Abdy received a new chip-enabled credit card. In order to activate the card, Abdy has to choose a PIN. Abdy has several PINs: one for his bank card, one to unlock his telephone, and some for his other credit cards. To make it easier to remember all his pass codes, Abdy always uses an arrangement of his birth date for his PIN. Abdy was born on January 7, 1996. Because of his birth date, Abdy always uses a 1 or a 7 for the first digit, a 9 or a 6 for the second digit, a 1 or a 7 for the third digit, and, finally, a 9 or a 6 for the last digit.
Using Abdy’s restrictions, how many different four-digit PINs are possible? ![]()
![]() Save your responses in your course folder.
Save your responses in your course folder.
Share 1
With a partner or in a group, discuss the following.
- How many PINs are possible?
- Was there a more efficient way used by one of the group members for determining the number of PINs rather than writing them all out?
- Apply the most efficient method you discussed to show how 10 000 possible four-digit PINs can be created when any digit from 0 to 9 can be used in any order.
![]() If required, save a copy of your discussion in your course folder.
If required, save a copy of your discussion in your course folder.
One possible way to solve this problem is to write out all the possible PINs. For example, one PIN could be 1676. You may decide on another appropriate strategy that you like better.
1.2. Explore
Module 8: Permutations, Combinations, and the Binomial Theorem
Explore
In Share 1, one of your group members may have suggested using a diagram to solve the PIN problem. The following diagram is called a tree diagram.
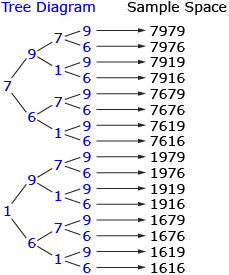
By counting the total number of terminal branches in the tree diagrams, you can see that Abdy has a choice of 16 different PINs. The list of all 16 possible PINs is called the sample space for this problem. The sample space is a list of all possible outcomes. You could also list all possible outcomes in an outcome table, such as the following one.
| First Digit | Second Digit | Third Digit | Fourth Digit |
| 7 | 9 | 7 | 9 |
| 7 | 9 | 7 | 6 |
| 1 | 9 | 7 | 9 |
| 1 | 9 | 7 | 6 |
| 7 | 6 | 7 | 9 |
| 7 | 6 | 7 | 6 |
| 1 | 6 | 7 | 9 |
| 1 | 6 | 7 | 6 |
| 7 | 9 | 1 | 9 |
| 7 | 9 | 1 | 6 |
| 1 | 9 | 1 | 9 |
| 1 | 9 | 1 | 6 |
| 7 | 6 | 1 | 9 |
| 7 | 6 | 1 | 6 |
| 1 | 6 | 1 | 9 |
| 1 | 6 | 1 | 6 |

die toss:Hemera/Thinkstock, coin toss: iStockphoto/Thinkstock
Read through Mathematics Glossary Tree Diagram to see how all possible outcomes of tossing a penny and rolling a die can be calculated by using a tree diagram. As you read, note that the order of tossing the penny or rolling the die does not affect the outcomes or sample space. Read the first example only in Mathematics Glossary Tree Diagram.
In Try This 2 you will find possible outcomes using tree diagrams and outcome tables. You will then determine an expression to calculate these outcomes.
Try This 2
Complete “Investigate Possible Arrangements” on pages 516 and 517 of the textbook.
![]() Save your responses in your course folder.
Save your responses in your course folder.
1.3. Explore 2
Module 8: Permutations, Combinations, and the Binomial Theorem
In question 4 of Try This 2 you were asked to make a conjecture about how you can use multiplication to determine the number of different possible outcomes.
To determine the total number of outfits possible, you will multiply the number of shirts by the number of pants and then multiply by the number of shoes or hats. In question 5 you need this product to be 1000 outfits. One possible solution is to have a choice of 10 shirts, 10 pairs of pants, and 10 pairs of shoes. The total number of outfits possible would be 10 × 10 × 10 = 1000.
For question 3.b. in Try This 2 you used a tree diagram to find the number of different outfits or outcomes. Your tree diagram may have looked similar to the diagram shown here.

This tree identified 16 different possible outfits from 4 pairs of pants, 2 shirts, and 2 hats. You may have noticed that you can also determine the total number of outfits possible by multiplying the number of pairs of pants by shirts and by hats: 4 × 2 × 2 = 16.
The fundamental counting principle tells you that if there are a ways to complete one task and b ways to complete another task, then there are a × b ways to complete the two tasks.
Think back to the example from Discover. For Abdy’s PIN, there were two choices for each space in the code. By using the fundamental counting principle, you can calculate the number of possible PINs.
2 × 2 × 2 × 2 = 16 possible PINs

Hemera/Thinkstock
If you would like to see another example of how a tree diagram and the fundamental counting principle are used to determine the number of outcomes, read through “Example 1: Method 1” on page 517 of the textbook.
1.4. Explore 3
Module 8: Permutations, Combinations, and the Binomial Theorem
Self-Check 1
-
Roger is choosing an outfit to wear for the day. He has a choice of 5 pairs of pants and 8 different shirts. How many different outfits can he choose? Answer

Jupiterimages/Brand X Pictures/Thinkstock
-
Use the following information to find the possible number of menu combinations.
The graduation council has been given the task of determining the menu for the graduation banquet. They have to select one salad, one main course, one side dish, one vegetable dish, and one dessert from the following choices.
salad: caesar, garden, tomato-herb, pasta
main course: chicken, beef, fish
side dish: rice, baked potato, mashed potato, French fries, pasta
vegetable: peas, corn, carrots, mixed vegetables, broccoli
dessert: cheesecake, pudding, ice cream, pie
Answer
-
How many routes are there from point A to point B if you always travel from left to right? Answer
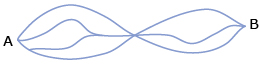
![]()
- Complete “Your Turn” on page 518 of the textbook. Answer
1.5. Explore 4
Module 8: Permutations, Combinations, and the Binomial Theorem
Try This 3

Purestock/Thinkstock
Ten children line up to go on the school bus. In how many ways can the children line up? Draw ten blanks to represent the ten places in line.
_ _ _ _ _ _ _ _ _ _
- How many possible children could be in the first spot in line?
- Now that one child has been placed first in line, how many possible children could be in the second spot?
- Finish determining the number of possibilities for each place in line.
- Use the fundamental counting principle to calculate the total number of ways the children can be lined up.

![]() Save your responses in your course folder.
Save your responses in your course folder.
1.6. Explore 5
Module 8: Permutations, Combinations, and the Binomial Theorem
As you realized in Try This 3, the fundamental counting principle can also be applied in situations where there are some choice restrictions. For example, if you want to determine the number of possible phone numbers, you need to know that you cannot use a zero as the first digit.
For many questions there is a more efficient way of calculating outcomes than drawing a tree diagram or creating an outcome table. In Try This 3 you investigated solving one problem by drawing blanks for the outcomes.

Courtesy of Alberta Motor Vehicles. Reproduced with permission
Another example to check out is how many license plates can be made with three letters (L) followed by three digits (D).
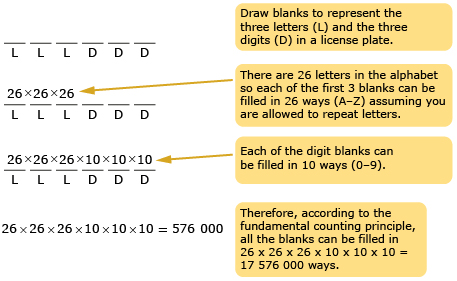
To view another example of using blanks to determine a solution, read "Example 1: Method 2" on page 518 of the textbook.
Self-Check 2

![]() Graham/25113263/flickr
Graham/25113263/flickr
Another way people are identified is by the license plate number on their vehicle. Historically, license plates in Alberta have consisted of three letters followed by three digits. Because the province is getting short of license plate numbers, Alberta is now changing the format to three letters followed by four digits. In 1997, Ontario switched from three digits followed by three letters to four letters followed by three digits.
- With a partner or in a group, determine how many more license plates are now available in Ontario with the fourth letter added. Answer
- You saw that the number of license plates in Alberta is 17 576 000 when the format is three letters followed by three digits. How many more license plates will be created in Alberta by adding the fourth digit? Answer
- Focus states that adding a new area code added a potential nine million more phone numbers in Alberta. How was this number calculated? Answer
![]()
- Do question 1 of “Check Your Understanding” on page 524 of the textbook. Answer
1.7. Explore 6
Module 8: Permutations, Combinations, and the Binomial Theorem
In Try This 3 you found that you could calculate the number of ways ten children could be lined up by finding the product of all consecutive natural numbers less than or equal to ten.
In mathematics there is a short-cut notation for the product of a positive integer, n, and all integers less than or equal to n. This short cut is called factorial notation and is denoted n!. Using factorial notation, the solution to Try This 3 would be that students can be lined up in 10! ways.
To learn more about how factorial notation works, work through Number of Arrangements. You will determine how many ways ten people can be arranged in the lineup. To begin, you will be asked to state how many people are available to fill the first spot in line. ![]()
Self-Check 3
- What is the value of 5!? Answer
- How can 6 × 5 × 4 × 3 × 2 × 1 be written using factorial notation? Answer
You have seen that 10! = 10 × 9 × 8 × 7 × 6 × 5 × 4 × 3 × 2 × 1.
If you let n = 10, then the expression can be written as the following:
n! = n × (n − 1) × (n − 2) × (n − 3) × (n − 4 ) × ( n − 5) × ( n − 6) × ( n − 7) × ( n − 8) × ( n − 9)
or
n! = n(n − 1)(n − 2)(n − 3)…(3)(2)(1)
Calculating the value of an expression involving factorial notation without a calculator can be time consuming. In Try This 4 you will look for patterns that might exist between subsequent expressions involving factorial notation.
Try This 4
- Complete the following table based on the information already available.
n!
n! in Expanded Form
Expression Involving n and
(n − 1)!Value of n!
1!
1
1
1
2!
2 × 1
2 × _!
2
3!
3 × 2 × 1
3 × _!
4!
_ × _ × _ × _
4 × _!
5!
_ × _ × _ × _ × _
5 × _!
6!
_ × _ × _ × _ × _ × _
6 × _!
7!
_ × _ × _ × _ × _ × _ × _
7 × _!
-
Describe the relationship between n! and (n − 1)!.
-
Create a general expression relating n!, n, and (n − 1)!.
![]() Save your responses in your course folder.
Save your responses in your course folder.
1.8. Explore 7
Module 8: Permutations, Combinations, and the Binomial Theorem
In Try This 4 you probably noticed that because n! represents the product of consecutive whole numbers, you can write a product in a variety of ways. For example, 10! can also be expressed as 10 x 9! or 10 x 9 x 8!.
Self-Check 4

iStockphoto/Thinkstock
Most calculators will have a factorial key, and usually the largest calculation they can do is 69! Try inputting 69! in your calculator and then see what happens when you try to enter 70!.
1.9. Explore 8
Module 8: Permutations, Combinations, and the Binomial Theorem
There are times when it is necessary to simplify factorial expressions. You will explore one way to simplify in Try This 5.
Try This 5
Find the value of ![]()
- Expand the numerator to show all the factors in 12!.
- Expand the denominator to show all the factors in 9!.
- Divide the numerator and denominator by any common factors.
- Calculate the solution by multiplying the remaining factors.
![]() Save your responses in your course folder.
Save your responses in your course folder.
1.10. Explore 9
Module 8: Permutations, Combinations, and the Binomial Theorem
As you may have noticed in Try This 5, writing out all the factors can take a long time. Here is another way you could simplify ![]()
Expanding the numerator and denominator gives you
As you can see, the expression in the brackets is the same as 9!. Therefore, you can write ![]() as
as ![]()
Dividing the numerator and denominator by the common factor of 9! leaves 12 x 11 x 10, or 1320.
Self-Check 5
Add factorial notation to your copy of Glossary Terms.
Add the following formulas or ideas to your copy of Formula Sheet:
- fundamental counting principle
- tree diagram
- factorial notation
1.11. Connect
Module 8: Permutations, Combinations, and the Binomial Theorem
Complete the Lesson 1 Assignment that you saved in your course folder at the beginning of this lesson. Show work to support your answers.
![]() Save your responses in your course folder.
Save your responses in your course folder.
Project Connection
You are ready to start working on Module 8 Project: Creating the Ultimate Password. Go to the Module 8 Project and read over all project requirements to become familiar with what you will be doing and how you will be assessed.
Complete Activity 1: Facts and Tips.
![]() Save your responses in your course folder.
Save your responses in your course folder.
1.12. Lesson 1 Summary
Module 8: Permutations, Combinations, and the Binomial Theorem
Lesson 1 Summary
In this lesson you learned how to determine the total number of outcomes in a sample space by using tree diagrams, outcome charts, and the fundamental counting principle. You also learned a short-cut notation called factorial notation. By using both the fundamental counting principle and factorial notation, you have seen that there are many ways to solve problems that involve arranging items and finding the possible number of arrangements.