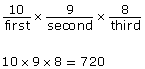Lesson 2
| Site: | MoodleHUB.ca 🍁 |
| Course: | Math 30-1 SS |
| Book: | Lesson 2 |
| Printed by: | Guest user |
| Date: | Tuesday, 9 December 2025, 11:17 PM |
Description
Created by IMSreader
1. Lesson 2
Module 8: Permutations, Combinations, and the Binomial Theorem
Lesson 2: Permutations
Focus

tag: iStockphoto/Thinkstock; SIN card: ![]() Creative Commons
Creative Commons
Attribution-Share Alike 3.0 Unported
One of your most important pieces of identification is your Social Insurance Number (SIN). This nine-digit number is used by the government to identify you.
The first digit in your SIN indicates the area of Canada where the card was issued. If the first digit is a 1, the number was issued in Atlantic Canada. Quebec gets 2 and 3, while 4 and 5 are for Ontario, 6 is for the Prairie provinces (Manitoba, Saskatchewan, and Alberta) and the Northwest Territories and Nunavut, 7 is for British Columbia and the Yukon, 9 is for temporary residents, and 8 and 0 are not used. Assuming there are no other restrictions, how many SINs are available to Alberta residents?
Lesson Outcomes
At the end of this lesson you will be able to
- determine the number of permutations of objects when
- not all objects are being arranged
- some objects are identical
- there are conditions on the permutations
- solve equations involving factorial notation
Lesson Questions
You will investigate the following questions:
- How can you determine the number of permutations when not all objects need to be arranged or some of the objects are identical?
- Are some counting methods more efficient than others in solving certain problems?
- How do you solve equations involving factorial notation?
Assessment
Your assessment may be based on a combination of the following tasks:
- completion of the Lesson 2 Assignment (Download the Lesson 2 Assignment and save it in your course folder now.)
- course folder submissions from Try This and Share activities
- additions to Glossary Terms and Formula Sheet
- work under Project Connection
1.1. Launch
Module 8: Permutations, Combinations, and the Binomial Theorem
Launch
Do you have the background knowledge and skills you need to complete this lesson successfully? Launch will help you find out.
Before beginning this lesson you should be able to factor quadratic equations of the form ax2 + bx + c = 0 where a = 1.
1.2. Are You Ready?
Module 8: Permutations, Combinations, and the Binomial Theorem
Are You Ready?
Solve the following equations. When solving quadratic equations you must rewrite the equation so that it equates to 0, and then factor the equation.
If you answered the Are You Ready? questions without difficulty, move to Discover.
If you found the Are You Ready? questions difficult, complete Refresher.
1.3. Refresher
Module 8: Permutations, Combinations, and the Binomial Theorem
Refresher
Watch the videos to review how to factor trinomials and solve quadratic equations.
“Factoring Trinomials 2” describes how to factor a trinomial with a non-1 leading coefficient.
“Solving Quadratic Equations 2” describes how to solve a quadratic equation by factoring.
Go back to the Are You Ready? section and try the questions again. If you are still having difficulty, contact your teacher.
1.4. Discover
Module 8: Permutations, Combinations, and the Binomial Theorem
Discover
You have used factorial notation to determine the number of permutations of n items taken n at a time, but what happens if you are only going to arrange some of the items?
Try This 1
Go to “Permutations.” You will explore the number of permutations when all items are chosen and when only some of the items are chosen.
- Change the “Number of Tiles in Box” and “Number of Draws from Box” to fill a chart similar to the following one. Use the “List” or “Tree” tab to view the possible permutations.
Number of Tiles in Box
Number of Draws from Box
Total Number of Possible Permutations
List Possible Permutations
2
2
2
AE, EA
2
1
2
A, E
3
3
3
2
3
1
4
4
Don’t list
4
3
Don’t list
4
2
Don’t list
4
1
5
5
Don’t list
5
4
Don’t list
5
3
Don’t list
5
2
Don’t list
5
1
-
Describe any patterns you noticed in the chart. Explain why the patterns might exist.
-
Would AEI and IEA each count as one possible permutation? Did the order the tiles were arranged in affect the number of possible permutations?

1.5. Explore
Module 8: Permutations, Combinations, and the Binomial Theorem
Explore

Jupiterimages/ Photos.com/Thinkstock
In Discover you saw different ways of calculating the number of permutations. The “Permutations” applet used lists, tree diagrams, and the fundamental counting principle. You also calculated the number of arrangements when you used all or some of the tiles.
In Lesson 1 you saw another way to calculate the number of permutations by drawing blanks to represent the problem.
In how many ways can horses finish first, second, and third if there are 10 horses in a race?
|
You can draw blanks to represent finishing first, second, and third. |
|
Assuming every horse is equally likely to win, you know the first position can be filled in ten ways. |
|
The second-place finisher could be any of the nine remaining horses. |
|
The third-place finisher could be any of the remaining eight horses. |
|
Applying the fundamental counting principle, the number of ways the first-, second-, and third-place positions could be filled is 10 × 9 × 8, or 720 different ways. |
Notice that the order of the finish is important. If three horses finish in the order A, B, and C, that order is a different result from a finish of C, B, and A, even though the arrangement contains all the same horses.
Try This 2
You know that if you’re trying to find the number of ways all ten horses could finish, it would be 10! = 10 × 9 × 8 × 7 × 6 × 5 × 4 × 3 × 2 × 1. Because you are only interested in the first three places, there is only 10 x 9 x 8. Is there a way to represent this information in factorial notation?
- Why are only three terms, 10 × 9 × 8, used to find the solution?
- 10 × 9 × 8 is no longer multiplied by the remaining factors, 7 × 6 × 5 × 4 × 3 × 2 × 1. What mathematical operation has to be performed on 7 × 6 × 5 × 4 × 3 × 2 × 1 so that the new product becomes 1?
- Write 7 × 6 × 5 × 4 × 3 × 2 × 1 in factorial notation.
- Write 10 × 9 × 8 as a quotient using factorial notation.

- Determine an expression for the denominator that uses the total number of horses, 10, and the number 3, which represents finding those that finished first, second, and third.
![]() Save your responses in your course folder.
Save your responses in your course folder.
Share 1
With a partner or group, share your solutions to questions 4 and 5. How do your quotients compare?
Based on your solution to question 5 in Try This 2, find a general expression for the number of permutations of n objects arranged r at a time.
![]() If required, save a record of this information in your course folder.
If required, save a record of this information in your course folder.
1.6. Explore 2
Module 8: Permutations, Combinations, and the Binomial Theorem

Hemera/Thinkstock
In Try This 2 you may have found that the problem can be represented by ![]()
In Try This 3 you will use the tile data you collected in Discover to work with the permutations formula.
Try This 3
- Retrieve your chart from Try This 1 and add one extra column,
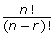 , to the chart as follows.
, to the chart as follows.
Number of Tiles in Box
Number of Draws from Box
Total Number of Possible Permutations
List Possible Permutations 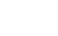
2
2
2
AE, EA
2
1
2
A, E
3
3
3
2
3
1
4
4
Don’t list
4
3
Don’t list
4
2
Don’t list
4
1
5
5
Don’t list
5
4
Don’t list
5
3
Don’t list
5
2
Don’t list
5
1
-
Determine which column represents n and which column represents r.

-
Complete the chart by calculating
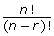 for the remaining rows. Show your work.
for the remaining rows. Show your work.
Special Note: 0! is defined as 1.
- In what instances could n! alone be used to calculate the number of permutations, and when must
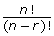 be used? Provide an example from the chart.
be used? Provide an example from the chart.
1.7. Explore 3
Module 8: Permutations, Combinations, and the Binomial Theorem
In Try This 3 you may have noticed that the ![]() column and the total number of possible permutations are the same. This formula provides you with a way to calculate the permutations without the need for tree diagrams or lists. In the next scenario you will see how blanks or the formula
column and the total number of possible permutations are the same. This formula provides you with a way to calculate the permutations without the need for tree diagrams or lists. In the next scenario you will see how blanks or the formula ![]() can be used to solve a problem.
can be used to solve a problem.
Consider the following scenario.
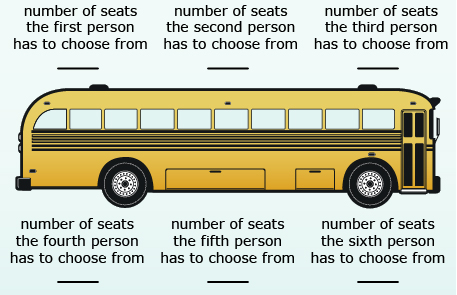
Six people are boarding an empty bus that has 30 seats. In how many different ways may the people be seated?
Solving the Problem Using Blanks
If you would like to solve this scenario by drawing blanks, draw your blanks for the elements that are most restricted. In this case there are fewer people on the bus than there are seats, so draw the blanks to represent each person. Then fill in the blanks with the number of seats the people may choose from.
iStockphoto/Thinkstock
Since the first person who gets on the bus has 30 seats to choose from, 30 is placed in the first blank. Now one seat is taken, so the second person has 29 seats to choose from, and so on.
When you complete this solution by filling in all six blanks, you get 30 × 29 × 28 × 27 × 26 × 25, or 427 518 000 ways.
Solving the Problem Using the Permutations Formula
In this example, n is 30 and represents the total number of seats; r is 6 and represents the number of people who choose a seat. You are finding the number of ways of choosing 6 items (r) from 30 items (n), which can be represented by
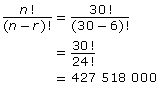
When you are presented with permutation questions, it is important to be able to identify n (the total number of objects there are to select from) and r (the number of objects being selected each time). Some questions will require you to do a little word deciphering to find these values. You can practise this deciphering as you solve the Self-Check problems.

Jupiterimages/Brand X Pictures/Thinkstock
Self-Check 1
- In how many ways can the president, vice-president, and secretary of a student council be selected from 30 people? Leave your answer in factorial form. Answer
- How many four-letter permutations can be formed from the word TRAVEL? State your answer in factorial notation and then evaluate the number of four-letter permutations. Answer
-
Consider the National Hockey League (NHL) playoffs. There are 15 teams in the Western Conference of the NHL. In how many ways can the conference quarterfinals be matched up? Keep in mind that in the quarterfinals the first-place team plays the eighth-place squad, second place plays seventh place, third place plays sixth place, and, finally, the fourth-place team plays the fifth-place finisher.

1.8. Explore 4
Module 8: Permutations, Combinations, and the Binomial Theorem

Hemera/Thinkstock
Drawing blanks and determining the number of ways they can be filled in works well when a small number of items is being arranged. But if a large number of items needs to be organized, drawing blanks can be a tedious and time-consuming method.
For example, 100 people line up for 50 audition spots on a talent show. In how many ways can the 50 audition spots be filled? You could draw 50 blanks and work to fill in the blanks, but you also know a formula that can be used to determine the number of permutations.
There are a total of 100 items, so n = 100.
From these 100 items only 50 are taken at a time, so r = 50.
Use the formula
If you recall, 69! is the largest factorial your calculator can calculate. To get around this issue, many graphing calculators are programmed to determine the number of permutations using a different notation, nPr, where
- n is still the total number of objects
- r is the number of objects you want in each arrangement
To calculate ![]() you would use 100P50 to calculate the number of permutations.
you would use 100P50 to calculate the number of permutations.
Investigate how to perform the permutation calculation on your calculator. You may need to reference the calculator’s guide or ask your teacher for assistance.
If the value of n and r are relatively small, you may solve nPr by simplifying the factorials.
Read part a. of “Example 2” on page 519 of the textbook.
The number of permutations of n objects taken r at a time is represented by nPr where 0 ≤ r ≤ n and ![]() Remember that 0! is defined as 1.
Remember that 0! is defined as 1.
Self-Check 2
Complete questions 2 and 4 from “Check Your Understanding” on page 524 of the textbook. Answer
1.9. Explore 5
Module 8: Permutations, Combinations, and the Binomial Theorem
Some permutation problems involve more than one case. When more than one case is involved, you must calculate the number of permutations in each case and add those numbers together. Here is an example involving cases.
Read “Example 5: Using Cases to Determine Permutations” on page 523 of the textbook. Notice that you add the number of permutations for each case.
View Permutations by the Case to see a full explanation of Example 5.

Self-Check 3
- Complete question 9 of “Check Your Understanding” from page 525 of the textbook. Answer
- Six people are going on a bus trip. They can use 2 buses, one for 12 passengers, and the other for 15 passengers. In how many ways may the people be arranged on one bus? Answer
Share 3
With a partner or in a group, discuss how the answer to Self-Check 3 would change if the passengers could use both buses and the 6 people could choose either bus.
1.10. Explore 6
Module 8: Permutations, Combinations, and the Binomial Theorem
Now that you have used the permutation formula, you may be asked to solve equations where n or r needs to be calculated. The ability to simplify and work with factorial expressions is important.
In Lesson 1 you practised expanding a factorial expression that included the variable n. The ability to expand factorial expressions helps to simplify expressions.
Simplify
Expand both the numerator and denominator.
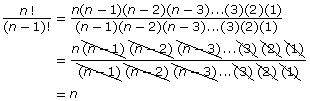
The only factor that did not divide out of the numerator and denominator was the n.
Self-Check 4
Simplify ![]() . Answer
. Answer
1.11. Explore 7
Module 8: Permutations, Combinations, and the Binomial Theorem
In Self-Check 4 you simplifed algebraic fractions involving factorial notation by dividing the numerator and the denominator by the same factors. For example,
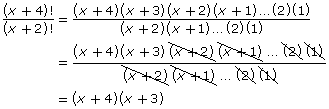
Or
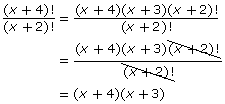
In a similar fashion you can simplify expressions with factorials to solve equations.
Solving a Factorial Equation shows you how to simplify an expression that includes factorials in order to solve an equation.

If you want to review another example of how to solve an equation that involves factorial notation, read part c. from “Example 2” on pages 519 and 520 of the textbook. In this example you will see how three different methods can be used to solve the equation. The method you have not yet seen is solving by graphing. Which method do you prefer?
Self-Check 5
- Solve for n.
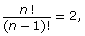 where n ∈ N. Answer
where n ∈ N. Answer
- Do “Your Turn” parts a. and c. on page 520 of the textbook. Answer
1.12. Explore 8
Module 8: Permutations, Combinations, and the Binomial Theorem
Watch “Solving Permutations 1” and “Solving Permutations 2” about how to solve nP2 = 6 and 8Pr = 56. Notice that in “Solving Permutations 2” the variable is in the denominator. Remember that when there is a variable in the denominator, non-permissible values are introduced.
You will now practise solving permutation equations where either n or r are not known.
Self-Check 6
Complete questions 7.a., 7.d., 22, and 23 from “Check Your Understanding” on pages 525 and 526 of the textbook. Answer
1.13. Explore 9
Module 8: Permutations, Combinations, and the Binomial Theorem
What happens if the items being arranged in a problem are not all different? Does this influence the number of permutations?
Sara and Mark are in math class and their teacher asks them to figure out how many different ways they can arrange the letters in their own names. Sara can only come up with 12 arrangements, but Mark can find 24 arrangements. They both have 4 letters in their name. Why did they get different answers? Is one student correct and one student incorrect?
Complete Try This 4 to explore why the same number of letters do not result in the same number of permutations.
Try This 4
A frequently used shorthand in texting is LOL. This acronym means “laughing out loud.”
- Using all letters from the phrase, form as many three-letter arrangements as possible.
- How many different arrangements do you see if you ignore the different colours in the arrangements?
- Why is there a difference between questions 1 and 2?
- What can you divide your answer from question 1 by to get the answer from question 2?
![]() Save your responses in your course folder.
Save your responses in your course folder.
1.14. Explore 10
Module 8: Permutations, Combinations, and the Binomial Theorem
In Try This 4 you probably noticed that when you ignore the different colours of the L letters, there are half as many permutations. There are three distinguishable permutations of the letters LOL.
You may have discovered the way to calculate the number of permutations of n objects where r objects are identical, s objects are identical, t objects are identical, and so on is![]() This formula is sometimes called the repetition formula.
This formula is sometimes called the repetition formula.
Now go back and think about the example with Sara and Mark. Why did they get different answers even though they have the same number of letters in their names?
Since she has the letter a twice in her name, Sara has 12 arrangements. She could find the number of arrangements by using the repetitions formula ![]() Mark has no repeating letters, so the number of arrangements he can find is 4!, or 24.
Mark has no repeating letters, so the number of arrangements he can find is 4!, or 24.
To review another example of how permutations with repeating objects can be calculated, go to page 521 of the textbook and read the question and solution for part a. of “Example 3.”
The idea of repeated elements can be used in other permutation problems. One permutation problem is Try This 5.
Try This 5
After their math class, Sara and Mark go to Mark’s house to study for their upcoming math test. They wonder if they can use the math they learned in class to figure out the number of routes they have to choose from to get from the school to Mark's house if they only travel east and south. Mark’s house is four blocks east and two blocks south of the school. Can you help them out?
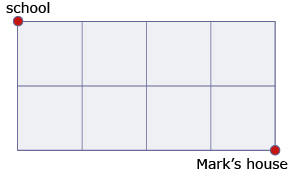
If you need some help to answer Try This 5, read part b. of “Example 3” on page 521 of the textbook.
1.15. Explore 11
Module 8: Permutations, Combinations, and the Binomial Theorem
Self-Check 7
Complete questions 8.b., 8.c., 17, and 21 from “Check Your Understanding” on pages 525 and 526 of the textbook. Answer
Add subset to your copy of Glossary Terms.
Add the following formulas to your copy of Formula Sheet:
- permutation formula
nPr where 0 ≤ r ≤ n and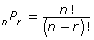
- repetition formula
The number of permutations of n objects when a objects are identical, b objects are identical, c objects are identical, and so on is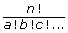 .
.
1.16. Connect
Module 8: Permutations, Combinations, and the Binomial Theorem
Complete the Lesson 2 Assignment that you saved in your course folder at the beginning of the lesson. Show work to support your answers.
![]() Save your responses in your course folder.
Save your responses in your course folder.
Project Connection
You are now ready to complete the next step of Module 8 Project: Creating the Ultimate Password.
Complete Activity 2: Creating Passwords.
![]() Save your responses in your course folder.
Save your responses in your course folder.
1.17. Lesson 2 Summary
Module 8: Permutations, Combinations, and the Binomial Theorem
Lesson 2 Summary
In this lesson you learned how to find the number of permutations of objects in several ways. These ways included making a list, drawing a tree diagram, drawing blanks, using the fundamental counting principle, and using the permutation formula, nPr. You learned that there are fewer permutations if there are identical items and that some methods of determining the number of permutations are better and more efficient than others depending upon the question posed.
In Lesson 3 you will learn about the number of choices of elements when order does not matter.