Mathematics 10-3 Module 6 Self Check

Module 6: Triangles and Other Polygons

Lesson 4

SC 4. Separate the triangles.

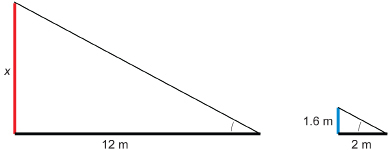
Are the triangles similar?

The two right triangles share an acute angle. Therefore, the triangles are similar.

Set up a proportion.

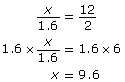
The height of the school is about 9.6 m.

SC 5. Are the right triangles similar?

Therefore, the triangles are similar.

Set up a proportion.

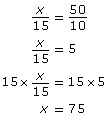
The width of the river is 75 m.

SC 6. There are four similar right triangles in the diagram. Let 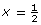the width of the balcony.

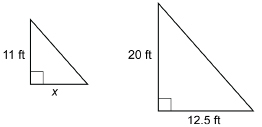
This illustration shows two right triangles with horizontal bases. The larger triangle has a base of 12.5 metres. The smaller triangle has a base of x metres. The right angles are at the left side of the triangles. The larger triangle has a vertical side of 20 feet. The smaller triangle has a vertical side of 11 feet. The upper angles of these triangles are the same.

Are the right triangles similar? The two right triangles share an acute angle. Therefore, the triangles are similar.

Set up a proportion.

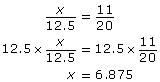
The chalet’s balcony width is 2 × 6.875 ft, or 13.75 ft.

SC 7.

This illustration shows two parallel line segments and two crossing segments that join them. The top parallel line has points A and B as the starting points for the second pair of line segments AD and BC. AD and BC cross at point E. Segment AE measures x inches. Segment ED measures 32 inches. Segment BE measures 12 inches. Segment EC measures 28 inches.

Do you need more practice using and reading symbols? If so, listen to the following statements read aloud:

“”
“”
“”

In

Since and 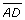is a transversal,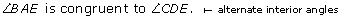

Therefore,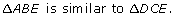
Set up a proportion.

Compare corresponding sides. Remember, corresponding sides lie opposite congruent angles.

Now x and 32 in are the measures opposite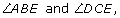 which are congruent.

So,

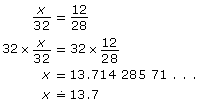
The missing side of the ironing board is approximately 13.7 in.

SC 8.

This illustration shows a right triangle with a horizontal base and a vertical side that measures 30 centimetres. A red square sits on the hypotenuse 20 centimetres from the lower end. A vertical segment is shown dropping from the box’s position on the hypotenuse. This vertical segment measures x centimetres.

Separate the triangles.

This illustration shows two triangles formed from the first triangle. One is a right triangle with a hypotenuse of 200 centimetres, and an angle marked with a single arc. The side opposite the marked angle measures 30 centimetres. The other triangle has a hypotenuse measuring 20 centimetres, and an angle marked with a single arc. The side opposite the marked angle measures x centimetres.

Set up a proportion.

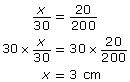
The timber is raised 3 cm off the ground.