Module 4: Lesson 8
Self-Check 3
Questions 5.a., 5.c., 6.b., and 6.d. on page 485 of the textbook
-
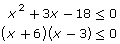
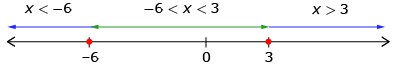
x < −6 −6 −6 < x < 3 3 x > 3 (x + 6) − 0 + + + (x – 3) − − − 0 + (x + 6)(x – 3) + 0 − 0 +
The solution is −6 ≤ x ≤ 3.
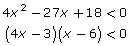
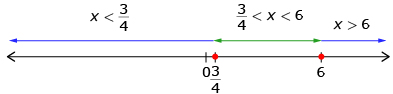
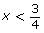
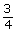
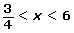
6 x > 6 (4x – 3) − 0 + + + (x – 6) − − − 0 + (4x – 3)(x – 6) + 0 − 0 +
The solution is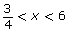 .
.
-
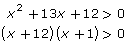
Case 1: positive × positive > 0
Case 2: negative × negative > 0
Case 1:
(x + 12) > 0 ∴ x > −12
The two red arrows meet up at x > −1, which is a solution.
(x + 1) > 0 ∴ x > −1

Case 2:
(x + 12) < 0 ∴ x < −12
The two red arrows meet up at x < −12, which is a solution.
(x + 1) < 0 ∴ x < −1

Therefore, the solution is x < −12 or x > −1.
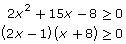
Case 1: positive × positive ≥ 0
Case 2: negative × negative ≥ 0
Case 1:
(2x − 1) ≥ 0 ∴
(x + 8) ≥ 0 ∴ x ≥ −8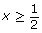
The red arrows meet up at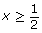 , which is a solution.
, which is a solution.

Case 2:
(2x − 1) ≤ 0 ∴
The red arrows meet up at x ≤ −8, which is a solution.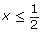
(x + 8) ≤ 0 ∴ x ≤ −8

Therefore, the solution is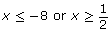 .
.