Lesson 8: Using Trigonometry to Find Missing Sides

Explore

Math 10C Module 1 Lesson 7

Module 1: Part 2 Trigonometry

Did You Know?

A tree farmer uses a clinometer to measure the angle between a horizontal line and the line of sight to the top of a tree. The farmer measures the distance to the base of the tree. Then the farmer uses the tangent ratio to calculate the height of the tree.

You have practiced finding the sine, cosine and tangent using triangles and by using your calculator. Let's use this knowledge to find missing sides in triangles.

Example

This shows a photo of the Muttart Gardens in Edmonton with right triangles drawn in the photo to show some possible lengths that could be calculated.

Finding Missing Sides

Consider one of the triangles in the picture above: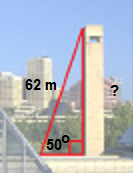

How could we find the height of the monument?

We know that sin is defined as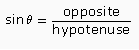

In this example, we know that the angle is 50^o, and the hypotenuse is 62 m.
The side opposite the 50^o is unknown so we can call it x.

If we replace this information in the equation we get

Now we need to think about how to solve for the unknown value x......
We need to get rid of the 62 in the denominator on the right. So since it is currently divided, we 'undo' the division by multiplying each side by 62.

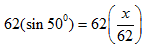
The 62's cancel on the right and we get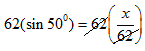

Now get a calculator out and finish
x = 62 x sin (50^o)
x = 47.5 m (Note we round to a reasonable number of decimals)

Pick a different triangle from the picture.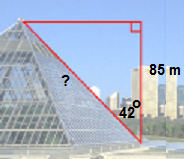

How would we find the slant height ( hypotenuse) of the glass pyramid?

Start by identifying what sides we are given or asked to find.
85m is the adjacent side and ? is the hypotenuse. We will call the unknown h.

So we could use cos to solve for the unknown.

Substitute in the values we know:

To solve this one, we will need to do two steps:
Step 1: Multiply each side by h to get rid of it in the denominator.

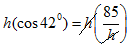
Step 2: Divide both sides by cos 42^o, so that the h is on the left by itself.

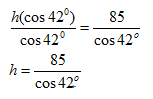
Grab your calculator and evaluate.

h = 85÷cos(42) enter
h = 114.4 m ( rounded again)

Self-Check

Now that you have some experience with using trigonometry to find missing sides, see how well you can answer the following questions.

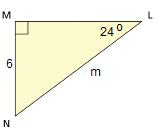
SC 1. In the following triangle, find the missing side m. Round to the nearest hundredth.

SC 2. In the following triangle, find the missing side c. Round to the nearest hundredth.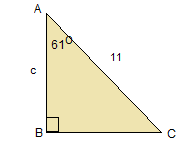

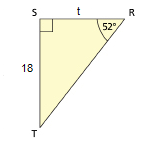
SC 3. Find the length of t in the following diagram. Round to the nearest hundredth.

SC4: Given the right triangle, XYZ, with <Z =90^o, <X = 22^o, and z = 14 cm, find x. Round to the nearest hundredth.

Compare your answers.