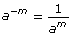Lesson 5: Integral Exponents
Module 2: Roots and Powers
 Watch and Listen
Watch and Listen
Use the “Negative Exponents” interactive to reinforce the discussion about negative exponents.
There are other ways of understanding negative exponents. The following chart presents two ways of verifying the result in the example using the laws of exponents.
|
Using the Quotient Law |
Using the Zero Exponent Law |
|
|
Two numbers are reciprocals of each other if their product is equal to 1. (for example, since
Therefore, |
The following examples show a practical way of thinking of negative exponents.
Example 1
Evaluate 2−3.
Solution
Look at
23 = 8
The reciprocal of 8 is 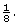
Therefore, 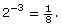
Example 2
Evaluate 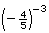
Solution
Look at
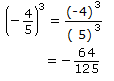
The reciprocal of 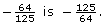
Therefore, 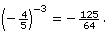
Example 3
Simplify 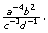
Solution
You can think of the expression as
![]()
![]()
 Tips
Tips
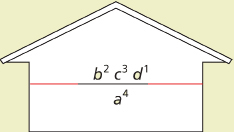
A fun way to think about negative exponents that can help you to simplify expressions easily is to view each power in the numerator and denominator as tenants in a house managed by you, the landlord.
In the case of the last example, there are four tenants: a−4 and b2 living upstairs, and c−3 and d−1 living downstairs.
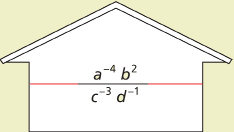
You can think of the sign of the exponents as a measure of how happy each tenant is with the surroundings. A positive exponent, as in the case of b2, means the tenant wants to stay put. A negative exponent, as in the case of a−4, c−3, and d−1, means the tenant is unhappy and looking to move to another floor.
As the landlord, you have the power to shuffle the tenants around. If you leave the powers with the positive exponents where they are (because they are happy tenants), and shuffle the powers with the negative exponents to either the denominator or the numerator (because they are unhappy in their present position), then you will get an equivalent expression with only positive exponents.
 Read
Read
Go to the textbook and work through the examples that deal with negative exponents. You will be focusing on questions that involve negative exponents, but you will also have to remember how to apply the other exponent laws you have previously learned. As you work through each step, try to identify the exponent law being applied.
Foundations and Pre-calculus Mathematics 10 (Pearson)
Read “Example 1: Evaluating Powers with Negative Integer Exponents” on page 231 and “Example 1: Simplifying Numerical Expressions with Rational Number Bases” and “Example 2: Simplifying Algebraic Expressions with Integer Exponents” on pages 238 and 239.
In Example 1.d) on page 239 you will see rational exponents or fractions as exponents. You will learn about rational exponents in the next lesson, but you can still apply the exponent laws you have learned thus far to solve this question. Give it a shot!
 Self-Check
Self-Check
Apply what you have learned to the following questions from your textbook. Remember that when you approach the task of simplifying exponents, there is often more than one way to do so. The solutions to the Self-Check questions show one method, but if you get the same result using a different method, then you may also be right. In those cases, check with your teacher to see if your method is mathematically sound.
Foundations and Pre-calculus Mathematics 10 (Pearson)
SC 1. Complete “Check Your Understanding” question 1 on page 231.
SC 2. Complete “Check Your Understanding” question 1 on page 238.
SC 3. Complete “Check Your Understanding” question 2 on page 239.
 Try This 1
Try This 1
Use the laws of exponents to solve the problems.
Complete the following questions in your course folder (binder).
Remember to show your work by indicating which laws you apply at each step. Also be sure to express your answers using positive exponents.
Foundations and Pre-calculus Mathematics 10 (Pearson)
TT 1. Complete the following:
a. “Exercises” questions 5, 8, 15 and 20 on pages 233 and 234
b. “Exercises” questions 4.b, 4.d, 7.b, 7.c, 8, 9, and 11.b. d on pages 241 to 243
Once you have completed these questions, use the link provided below to check your work.
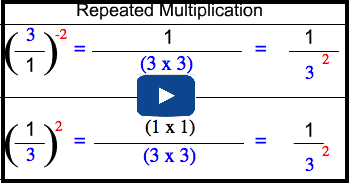
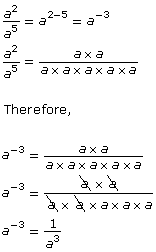
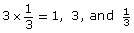 are reciprocals of each other)
are reciprocals of each other)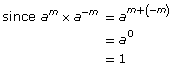
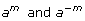 are reciprocals of each other
are reciprocals of each other